Back to the topics list

мешани броеви, мешани дропки

Што се мешани дропки?

Мешана дропка е цел број, а соодветна дропка претставена заедно. Генерално претставува број помеѓу кои било два цели броја.

Мешаните дропки се познати и како мешани броеви.

Погледнете ја дадената слика таа претставува дропка што е поголема од 1, но помала од 2. Така, тоа е мешан број, еднаков на \(1\frac{3}{4}\)

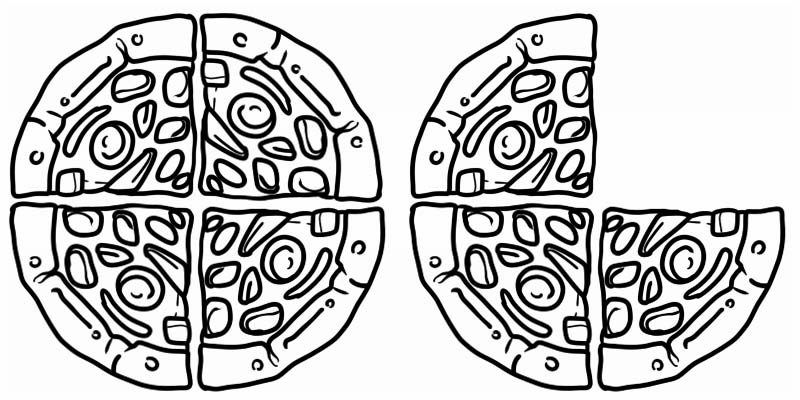
Некои други примери на мешани броеви се:

\(3\frac{1}{2}\)

\(2\frac{3}{5}\)

\(5\frac{3}{5}\)

\(4\frac{1}{5}\)

Делови од мешан број

Мешан број се формира со комбинирање на три дела: цел број, броител и именител. Бротелот и именителот се дел од соодветната дропка што го прави мешаниот број.

Во мешаниот број \(3\frac{1}{2}\)

• 3 е целиот број
• \(\frac{1}{2}\) е дропка, каде што 1 е броител, а 2 е именителот

Својства на мешани броеви

• Тоа е делумно цел број
• Тоа е делумно дропка

Претворање на неправилна дропка во мешани фракции

Чекор 1: Поделете го броителот со именителот

Чекор 2: Запишете го количникот како цел број

Чекор 3: Запишете го остатокот како броител и делителот како именител

На пример, ги следиме дадените чекори за да го претвориме \(\frac{7}{3}\) во формулар со мешани броеви.

Чекор 1: Поделете 7 со 3

Чекор 2: Напишете количник, делител и остаток во форма на мешан број: \(2\frac{1}{3}\)

Додавање или одземање мешани дропки

Може да се собираат (или одземаат) измешаните броеви со преуредување на цели броеви, нивно собирање (или одземање) одделно и собирање на преостанатите дропки поединечно и на крајот комбинирајќи ги сите.

\(1\frac{1}{2} + 3\frac{3}{4} \)

Собирање на цели броеви одделно и дропки одделно.

За цели броеви:

1 + 3 = 4

За дропки: Најдете го LCM и потоа додадете

\(\frac{1}{2} + \frac{3}{4}\)

= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)

= \(\frac{2}{4} + \frac{3}{4}\)

= \(\frac{5}{4}\)

Конвертирање на неправилната дропка во мешан број: \(\frac{5}{4} = 1\frac{1}{4}\)

На крајот, додавајќи ги двата дела заедно.

\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)

Одземање мешани дропки

Само следете го истиот метод (како за додавање), но одземете наместо додавање:

Пример: \(15\frac{3}{4} - 8\frac{5}{6}\)

Претвори во несоодветни дропки: \(\frac{63}{4} - \frac{53}{6}\)

Заеднички именител (LCM од 4 и 6) од 12: \(\frac{189}{12} - \frac{106}{12}\)

Сега одземете: \(\frac{83}{12}\)

Промени во мешана дропка: \(6\frac{11}{12}\)

Множење мешани дропки

• Променете ја секоја измешана дропка во неправилна дропка
• Поедноставете ако е можно
• Помножете ги броителите, а потоа именителот
• Наведете го одговорот со најниски зборови
• Проверете за да бидете сигурни дека одговорот има смисла

Пример: \(5\frac{2}{3} \times \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{1}{4}\)

= \(\frac{17}{12}\)

= \(1\frac{5}{12}\)

Делење мешани фракции

• Променете ја секоја измешана дропка во неправилна дропка
• Помножете се со реципроцитет на делителот, поедноставувајќи ако е можно
• Наведете го одговорот со најниски зборови
• Проверете за да бидете сигурни дека одговорот има смисла

Пример:

\(5\frac{2}{3} \div \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{4}{1}\)

= \(\frac{68}{3}\)

= \(22\frac{2}{3}\)