Back to the topics list

холимог тоо, холимог фракц

Холимог бутархай гэж юу вэ?

Холимог бутархай нь бүхэл тоо бөгөөд зөв бутархайг хамтад нь илэрхийлнэ. Энэ нь ерөнхийдөө дурын хоёр бүхэл тооны хоорондох тоог илэрхийлдэг.

Холимог бутархайг холимог тоо гэж бас нэрлэдэг.

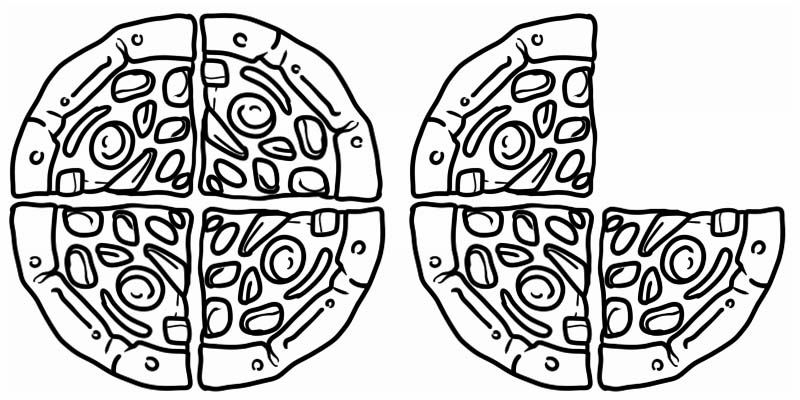
Өгөгдсөн зургийг харвал 1-ээс их боловч 2-оос бага бутархайг илэрхийлж байна. Тиймээс энэ нь \(1\frac{3}{4}\) -тэй тэнцүү холимог тоо юм.

Холимог тоонуудын бусад жишээнүүд нь:

\(3\frac{1}{2}\)

\(2\frac{3}{5}\)

\(5\frac{3}{5}\)

\(4\frac{1}{5}\)

Холимог тооны хэсгүүд

Бүхэл тоо, хүртэгч, хуваагч гэсэн гурван хэсгийг нийлүүлснээр холимог тоо үүсдэг. Тоолуур ба хуваагч нь холимог тоог үүсгэдэг зөв бутархайн хэсэг юм.

Холимог тоонд \(3\frac{1}{2}\)

• 3 нь бүхэл тоо юм
• \(\frac{1}{2}\) нь бутархай бөгөөд 1 нь тоологч, 2 нь хуваагч юм

Холимог тоонуудын шинж чанарууд

• Энэ нь хэсэгчлэн бүхэл тоо юм
• Энэ нь хэсэгчлэн бутархай юм

Буруу бутархайг холимог бутархай болгон хувиргах

Алхам 1: Тоолуурыг хуваагчаар хуваана

Алхам 2: Хэсэлтийг бүхэл тоо болгон бич

Алхам 3: Үлдэгдлийг тоологчоор, хуваагчийг хуваагчаар бичнэ үү.

Жишээлбэл, бид \(\frac{7}{3}\) -г холимог тооны хэлбэрт хөрвүүлэхийн тулд өгөгдсөн алхмуудыг дагаж мөрддөг.

Алхам 1: 7-г 3-т хуваа

Алхам 2: Холимог тоо хэлбэрээр хуваагч, үлдэгдлийг хуваагч, үлдэгдлийг бичнэ үү: \(2\frac{1}{3}\)

Холимог бутархайг нэмэх, хасах

Холимог тоог бүхэл тоог дахин цэгцлэх, тусад нь нэмэх (эсвэл хасах) болон үлдсэн бутархайг тус тусад нь нэмж, эцэст нь бүгдийг нэгтгэх замаар холимог тоог нэмж (эсвэл хасах) болно.

\(1\frac{1}{2} + 3\frac{3}{4} \)

Бүхэл тоог тусад нь, бутархайг тус тусад нь нэмнэ.

Бүхэл тоонуудын хувьд:

1 + 3 = 4

Бутархайн хувьд: LCM-г олоод нэм

\(\frac{1}{2} + \frac{3}{4}\)

= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)

= \(\frac{2}{4} + \frac{3}{4}\)

= \(\frac{5}{4}\)

Бутархай бутархайг холимог тоо болгон хувиргах: \(\frac{5}{4} = 1\frac{1}{4}\)

Төгсгөлд нь хоёр хэсгийг хамтад нь нэмнэ.

\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)

Холимог бутархайг хасах

Зүгээр л ижил аргыг (нэмэх гэх мэт) дага, гэхдээ нэмэхийн оронд хасах:

Жишээ: \(15\frac{3}{4} - 8\frac{5}{6}\)

Бутархай бутархай руу хөрвүүлэх: \(\frac{63}{4} - \frac{53}{6}\)

12-ын нийтлэг хуваагч (4 ба 6-н LCM): \(\frac{189}{12} - \frac{106}{12}\)

Одоо хасах: \(\frac{83}{12}\)

Холимог бутархай болгон өөрчлөх: \(6\frac{11}{12}\)

Холимог бутархайг үржүүлэх

• Холимог бутархай бүрийг буруу бутархай болгон өөрчил
• Боломжтой бол хялбарчил
• Тоолуур, дараа нь хуваагчийг үржүүлнэ
• Хариултыг хамгийн бага үгээр илэрхийлнэ үү
• Хариулт нь утга учиртай эсэхийг шалгаарай

Жишээ: \(5\frac{2}{3} \times \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{1}{4}\)

= \(\frac{17}{12}\)

= \(1\frac{5}{12}\)

Холимог бутархайг хуваах

• Холимог бутархай бүрийг буруу бутархай болгон өөрчил
• Боломжтой бол хялбарчлах, хуваагчийн эсрэгээр үржүүлнэ
• Хариултыг хамгийн бага үгээр илэрхийлнэ үү
• Хариулт нь утга учиртай эсэхийг шалгаарай

Жишээ:

\(5\frac{2}{3} \div \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{4}{1}\)

= \(\frac{68}{3}\)

= \(22\frac{2}{3}\)