मिश्रित अंश एक पूर्ण संख्या हो, र एक उचित अंश सँगै प्रतिनिधित्व हुन्छ। यसले सामान्यतया कुनै पनि दुई पूर्ण संख्याहरू बीचको संख्यालाई प्रतिनिधित्व गर्दछ।
मिश्रित अंशहरूलाई मिश्रित संख्याहरू पनि भनिन्छ।
दिइएको छविमा हेर्नुहोस् यसले १ भन्दा ठुलो तर २ भन्दा कमको अंशलाई प्रतिनिधित्व गर्दछ। यसरी यो मिश्रित संख्या हो, बराबर \(1\frac{3}{4}\)
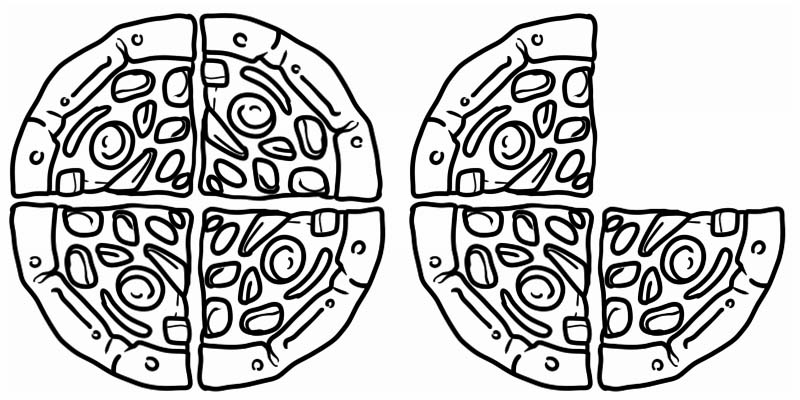
मिश्रित संख्याका केही अन्य उदाहरणहरू हुन्:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
एक मिश्रित संख्या तीन भागहरू संयोजन गरेर बनाइन्छ: एक पूर्ण संख्या, एक अंश, र एक भाजक। अंश र भाजक उचित अंशको अंश हुन् जसले मिश्रित संख्या बनाउँछ।
मिश्रित संख्यामा \(3\frac{1}{2}\)
चरण 1: अंकलाई भाजकद्वारा विभाजित गर्नुहोस्
चरण 2: पूर्ण संख्याको रूपमा भागफल लेख्नुहोस्
चरण 3: शेषलाई अंशको रूपमा र भाजकलाई भाजकको रूपमा लेख्नुहोस्
उदाहरणका लागि, हामी \(\frac{7}{3}\) मिश्रित संख्या फारममा रूपान्तरण गर्न दिइएको चरणहरू पालना गर्छौं।
चरण 1: 7 लाई 3 ले विभाजन गर्नुहोस्
चरण 2: मिश्रित संख्या फारममा भागफल, भाजक र शेष लेख्नुहोस्: \(2\frac{1}{3}\)
एकले मिश्रित संख्याहरू थप्न (वा घटाउन) पूरै संख्याहरूलाई पुन: व्यवस्थित गरेर, तिनीहरूलाई छुट्टै थपेर (वा घटाएर) र बाँकी रहेका अंशहरूलाई व्यक्तिगत रूपमा थप्न र अन्तमा ती सबैलाई जोड्न सक्छ।
\(1\frac{1}{2} + 3\frac{3}{4} \)
पूरै संख्याहरू छुट्टाछुट्टै र अंशहरू छुट्टाछुट्टै जोड्दै।
पूर्ण संख्याहरूको लागि:
१ + ३ = ४
अंशका लागि: LCM फेला पार्नुहोस् र त्यसपछि थप्नुहोस्
\(\frac{1}{2} + \frac{3}{4}\)
\(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
\(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
अनुचित अंशलाई मिश्रित संख्यामा रूपान्तरण गर्दै: \(\frac{5}{4} = 1\frac{1}{4}\)
अन्तमा, दुबै भागहरू सँगै जोड्नुहोस्।
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
केवल एउटै विधि (जस्तै थप्नको लागि) पछ्याउनुहोस्, तर थप्नुको सट्टा घटाउनुहोस्:
उदाहरण: \(15\frac{3}{4} - 8\frac{5}{6}\)
अनुचित अंशहरूमा रूपान्तरण गर्नुहोस्: \(\frac{63}{4} - \frac{53}{6}\)
१२ को साधारण भाजक (४ र ६ को LCM): \(\frac{189}{12} - \frac{106}{12}\)
अब घटाउनुहोस्: \(\frac{83}{12}\)
मिश्रित अंशमा परिवर्तन गर्नुहोस्: \(6\frac{11}{12}\)
उदाहरण: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
उदाहरण:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)