Een gemengde breuk is een geheel getal en een juiste breuk wordt samen weergegeven. Het vertegenwoordigt over het algemeen een getal tussen twee willekeurige hele getallen.
Gemengde breuken worden ook wel gemengde getallen genoemd.
Kijk naar de gegeven afbeelding, het vertegenwoordigt een breuk die groter is dan 1 maar kleiner dan 2. Het is dus een gemengd getal, gelijk aan \(1\frac{3}{4}\)
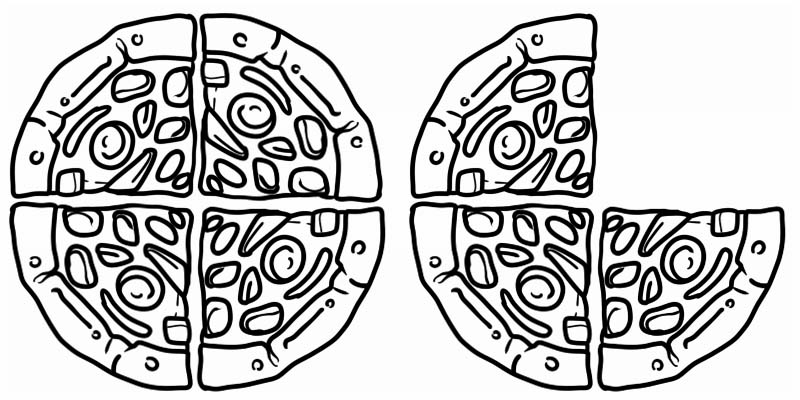
Enkele andere voorbeelden van gemengde getallen zijn:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Een gemengd getal wordt gevormd door drie delen te combineren: een geheel getal, een teller en een noemer. De teller en noemer maken deel uit van de juiste breuk die het gemengde getal vormt.
In het gemengde getal \(3\frac{1}{2}\)
Stap 1: Deel de teller door de noemer
Stap 2: Schrijf het quotiënt op als het gehele getal
Stap 3: Schrijf de rest op als teller en de deler als noemer
We volgen bijvoorbeeld de gegeven stappen om \(\frac{7}{3}\) om te zetten in een gemengde getalvorm.
Stap 1: deel 7 door 3
Stap 2: Schrijf quotiënt, deler en rest in de gemengde getalvorm: \(2\frac{1}{3}\)
Men kan gemengde getallen optellen (of aftrekken) door de gehele getallen te herschikken, ze afzonderlijk op te tellen (of af te trekken) en de overgebleven breuken afzonderlijk op te tellen en ze uiteindelijk allemaal te combineren.
\(1\frac{1}{2} + 3\frac{3}{4} \)
De gehele getallen afzonderlijk optellen en de breuken afzonderlijk.
Voor hele getallen:
1 + 3 = 4
Voor breuken: zoek de LCM en tel vervolgens op
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
De onechte breuk omzetten in een gemengd getal: \(\frac{5}{4} = 1\frac{1}{4}\)
Uiteindelijk beide delen bij elkaar opgeteld.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Volg gewoon dezelfde methode (zoals voor optellen), maar trek af in plaats van optellen:
Voorbeeld: \(15\frac{3}{4} - 8\frac{5}{6}\)
Converteren naar onechte breuken: \(\frac{63}{4} - \frac{53}{6}\)
De gemene deler (LCM van 4 en 6) van 12: \(\frac{189}{12} - \frac{106}{12}\)
Trek nu af: \(\frac{83}{12}\)
Verander in een gemengde breuk: \(6\frac{11}{12}\)
Voorbeeld: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Voorbeeld:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)