Ułamek mieszany to liczba całkowita i ułamek właściwy reprezentowany razem. Zwykle reprezentuje liczbę między dowolnymi dwiema liczbami całkowitymi.
Ułamki mieszane są również znane jako liczby mieszane.
Spójrz na podany obrazek, przedstawia on ułamek większy niż 1, ale mniejszy niż 2. Jest to zatem liczba mieszana równa \(1\frac{3}{4}\)
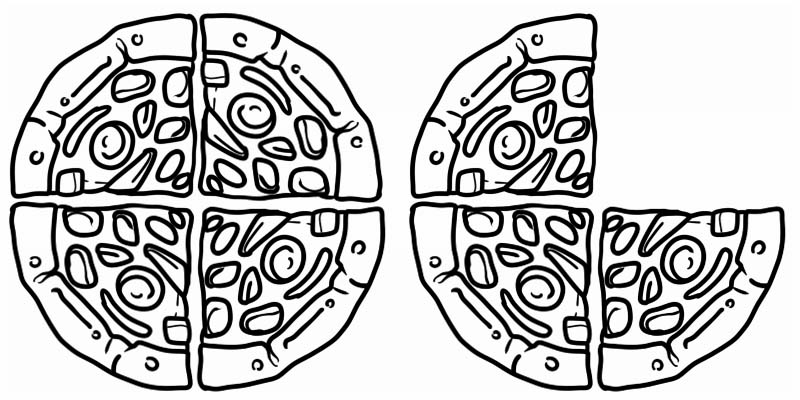
Inne przykłady liczb mieszanych to:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Liczbę mieszaną tworzy się przez połączenie trzech części: liczby całkowitej, licznika i mianownika. Licznik i mianownik są częścią właściwego ułamka, który tworzy liczbę mieszaną.
W liczbie mieszanej \(3\frac{1}{2}\)
Krok 1: Podziel licznik przez mianownik
Krok 2: Zapisz iloraz jako liczbę całkowitą
Krok 3: Zapisz resztę jako licznik, a dzielnik jako mianownik
Na przykład postępujemy zgodnie z podanymi krokami, aby przekonwertować \(\frac{7}{3}\) na postać liczb mieszanych.
Krok 1: Podziel 7 przez 3
Krok 2: Zapisz iloraz, dzielnik i resztę w postaci liczby mieszanej: \(2\frac{1}{3}\)
Liczby mieszane można dodawać (lub odejmować), przestawiając liczby całkowite, dodając (lub odejmując) je osobno i dodając pozostałe ułamki indywidualnie, a na koniec łącząc je wszystkie.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Dodawanie liczb całkowitych osobno i osobno ułamków.
Dla liczb całkowitych:
1 + 3 = 4
Dla ułamków: Znajdź LCM, a następnie dodaj
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Zamiana ułamka niewłaściwego na liczbę mieszaną: \(\frac{5}{4} = 1\frac{1}{4}\)
Na koniec dodaj obie części do siebie.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Po prostu postępuj zgodnie z tą samą metodą (jak w przypadku dodawania), ale odejmij zamiast dodawać:
Przykład: \(15\frac{3}{4} - 8\frac{5}{6}\)
Zamień na ułamki niewłaściwe: \(\frac{63}{4} - \frac{53}{6}\)
Wspólny mianownik (LCM 4 i 6) liczby 12: \(\frac{189}{12} - \frac{106}{12}\)
Teraz odejmij: \(\frac{83}{12}\)
Zamień na ułamek mieszany: \(6\frac{11}{12}\)
Przykład: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Przykład:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)