Uma fração mista é um número inteiro e uma fração própria representada em conjunto. Geralmente representa um número entre quaisquer dois números inteiros.
As frações mistas também são conhecidas como números mistos.
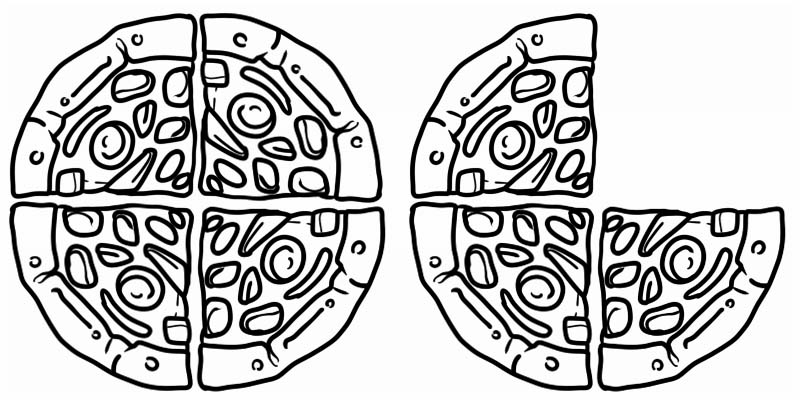
Observe a imagem dada, ela representa uma fração maior que 1, mas menor que 2. É, portanto, um número misto, igual a \(1\frac{3}{4}\)
Alguns outros exemplos de números mistos são:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Um número misto é formado pela combinação de três partes: um número inteiro, um numerador e um denominador. O numerador e o denominador fazem parte da fração própria que compõe o número misto.
No número misto \(3\frac{1}{2}\)
Passo 1: Divida o numerador pelo denominador
Passo 2: Anote o quociente como o número inteiro
Passo 3: Escreva o resto como numerador e o divisor como denominador
Por exemplo, seguimos as etapas fornecidas para converter \(\frac{7}{3}\) em uma forma de número misto.
Passo 1: Divida 7 por 3
Etapa 2: escreva quociente, divisor e resto na forma de número misto: \(2\frac{1}{3}\)
Pode-se adicionar (ou subtrair) números mistos reorganizando os números inteiros, adicionando (ou subtraindo) separadamente e adicionando as frações restantes individualmente e no final combinando todos eles.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Adicionando os números inteiros separadamente e as frações separadamente.
Para números inteiros:
1 + 3 = 4
Para frações: encontre o MMC e, em seguida, adicione
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Convertendo a fração imprópria em um número misto: \(\frac{5}{4} = 1\frac{1}{4}\)
No final, juntando as duas partes.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Basta seguir o mesmo método (como para adicionar), mas subtrair em vez de adicionar:
Exemplo: \(15\frac{3}{4} - 8\frac{5}{6}\)
Converter em frações impróprias: \(\frac{63}{4} - \frac{53}{6}\)
O denominador comum (LCM de 4 e 6) de 12: \(\frac{189}{12} - \frac{106}{12}\)
Agora subtraia: \(\frac{83}{12}\)
Mude para uma fração mista: \(6\frac{11}{12}\)
Exemplo: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Exemplo:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)