Смешанная дробь — это целое число и правильная дробь, представленные вместе. Обычно представляет собой число между любыми двумя целыми числами.
Смешанные дроби также известны как смешанные числа.
Посмотрите на данное изображение, оно представляет дробь, которая больше 1, но меньше 2. Таким образом, это смешанное число, равное \(1\frac{3}{4}\)
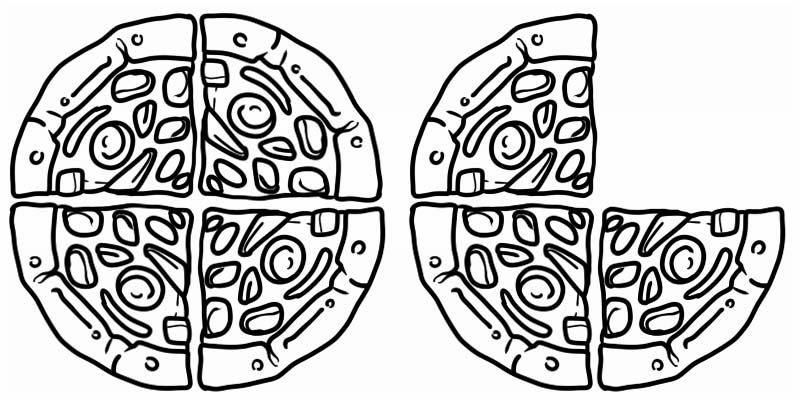
Некоторые другие примеры смешанных чисел:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Смешанное число образуется путем сложения трех частей: целого числа, числителя и знаменателя. Числитель и знаменатель являются частью правильной дроби, составляющей смешанное число.
В смешанном числе \(3\frac{1}{2}\)
Шаг 1: разделите числитель на знаменатель
Шаг 2: Запишите частное как целое число
Шаг 3: Запишите остаток как числитель и делитель как знаменатель
Например, мы следуем данным шагам, чтобы преобразовать \(\frac{7}{3}\) в смешанную числовую форму.
Шаг 1: Разделите 7 на 3.
Шаг 2: Запишите частное, делитель и остаток в форме смешанного числа: \(2\frac{1}{3}\)
Можно складывать (или вычитать) смешанные числа, переставляя целые числа, добавляя (или вычитая) их по отдельности и добавляя оставшиеся дроби по отдельности и, в конце концов, объединяя их все.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Сложение целых чисел отдельно и дробей отдельно.
Для целых чисел:
1 + 3 = 4
Для дробей: найдите НОК, а затем добавьте
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Преобразование неправильной дроби в смешанное число: \(\frac{5}{4} = 1\frac{1}{4}\)
В конце складываем обе части вместе.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Просто следуйте тому же методу (например, для сложения), но вычитайте вместо добавления:
Пример: \(15\frac{3}{4} - 8\frac{5}{6}\)
Преобразование в неправильные дроби: \(\frac{63}{4} - \frac{53}{6}\)
Общий знаменатель (НОК 4 и 6) числа 12: \(\frac{189}{12} - \frac{106}{12}\)
Теперь вычтите: \(\frac{83}{12}\)
Превратить в смешанную дробь: \(6\frac{11}{12}\)
Пример: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Пример:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)