Back to the topics list

blandad fraktion, blandade siffror

Vad är blandade fraktioner?

En blandad bråkdel är ett heltal och en egen bråkdel representerad tillsammans. Det representerar vanligtvis ett tal mellan två heltal.

Blandade bråk är också kända som blandade tal.

Titta på den givna bilden den representerar en bråkdel som är större än 1 men mindre än 2. Det är alltså ett blandat tal, lika med \(1\frac{3}{4}\)

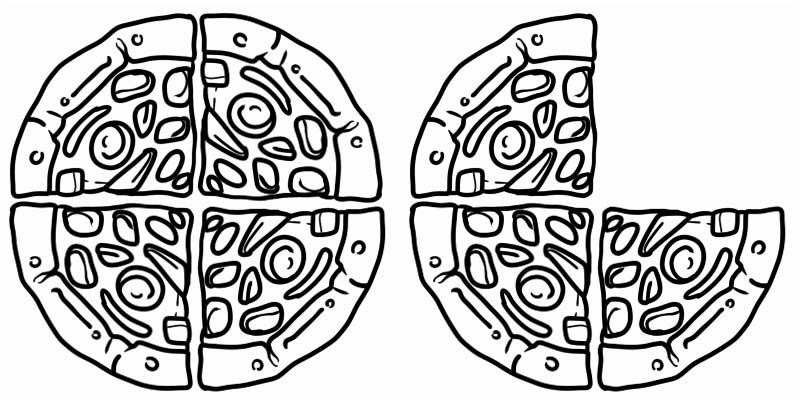
Några andra exempel på blandade tal är:

\(3\frac{1}{2}\)

\(2\frac{3}{5}\)

\(5\frac{3}{5}\)

\(4\frac{1}{5}\)

Delar av ett blandat nummer

Ett blandat tal bildas genom att kombinera tre delar: ett heltal, en täljare och en nämnare. Täljaren och nämnaren är en del av det egenbråk som gör det blandade talet.

I det blandade talet \(3\frac{1}{2}\)

• 3 är hela talet
• \(\frac{1}{2}\) är ett bråk, där 1 är täljaren och 2 är nämnaren

Egenskaper för blandade tal

• Det är delvis ett heltal
• Det är delvis en bråkdel

Konvertera oegentlig fraktion till blandade fraktioner

Steg 1: Dividera täljaren med nämnaren

Steg 2: Skriv ner kvoten som ett heltal

Steg 3: Skriv ner resten som täljare och divisor som nämnare

Till exempel följer vi de givna stegen för att konvertera \(\frac{7}{3}\) till en blandad talform.

Steg 1: Dividera 7 med 3

Steg 2: Skriv kvot, divisor och rest i den blandade talformen: \(2\frac{1}{3}\)

Addera eller subtrahera blandade fraktioner

Man kan lägga till (eller subtrahera) blandade tal genom att ordna om hela talen, lägga till (eller subtrahera) dem separat och lägga till de överblivna bråken individuellt och i slutändan kombinera dem alla.

\(1\frac{1}{2} + 3\frac{3}{4} \)

Lägga till hela talen separat och bråken separat.

För heltal:

1 + 3 = 4

För bråk: Hitta LCM och lägg sedan till

\(\frac{1}{2} + \frac{3}{4}\)

= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)

= \(\frac{2}{4} + \frac{3}{4}\)

= \(\frac{5}{4}\)

Konvertera det oegentliga bråket till ett blandat tal: \(\frac{5}{4} = 1\frac{1}{4}\)

I slutändan lägger man ihop båda delarna.

\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)

Subtrahera blandade fraktioner

Följ bara samma metod (som för att lägga till), men subtrahera istället för att lägga till:

Exempel: \(15\frac{3}{4} - 8\frac{5}{6}\)

Konvertera till oegentliga bråk: \(\frac{63}{4} - \frac{53}{6}\)

Den gemensamma nämnaren (LCM av 4 och 6) av 12: \(\frac{189}{12} - \frac{106}{12}\)

Subtrahera nu: \(\frac{83}{12}\)

Ändra till en blandad bråkdel: \(6\frac{11}{12}\)

Multiplicera blandade fraktioner

• Ändra varje blandad fraktion till en felaktig fraktion
• Förenkla om möjligt
• Multiplicera täljarna och sedan nämnarna
• Sätt svaret i lägsta termer
• Kontrollera att svaret är vettigt

Exempel: \(5\frac{2}{3} \times \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{1}{4}\)

= \(\frac{17}{12}\)

= \(1\frac{5}{12}\)

Dela blandade fraktioner

• Ändra varje blandad fraktion till en felaktig fraktion
• Multiplicera med den reciproka av divisorn, förenkla om möjligt
• Sätt svaret i lägsta termer
• Kontrollera att svaret är vettigt

Exempel:

\(5\frac{2}{3} \div \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{4}{1}\)

= \(\frac{68}{3}\)

= \(22\frac{2}{3}\)