เศษส่วนคละเป็นจำนวนเต็มและเศษส่วนที่เหมาะสมแสดงร่วมกัน โดยทั่วไปจะแทนจำนวนระหว่างจำนวนเต็มสองจำนวนใดๆ
เศษส่วนคละเรียกอีกอย่างว่าจำนวนคละ
ดูภาพที่กำหนดให้แทนเศษส่วนที่มากกว่า 1 แต่น้อยกว่า 2 จึงเป็นจำนวนคละ เท่ากับ \(1\frac{3}{4}\)
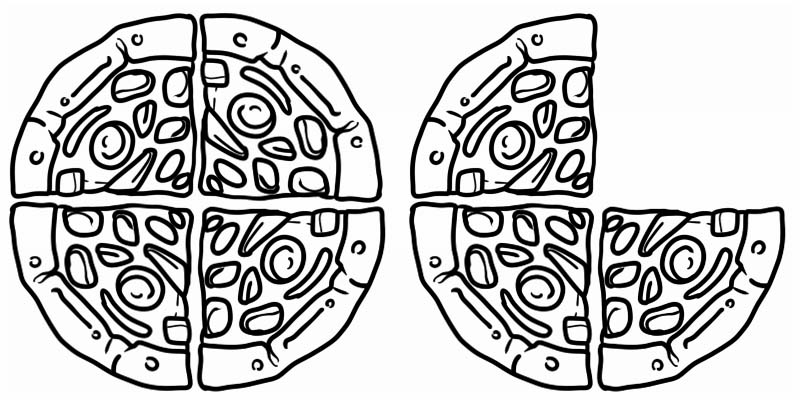
ตัวอย่างอื่นๆ ของจำนวนคละ ได้แก่
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
จำนวนคละเกิดจากการนำสามส่วนมารวมกัน ได้แก่ จำนวนเต็ม ตัวเศษ และตัวส่วน ตัวเศษและตัวส่วนเป็นส่วนหนึ่งของเศษส่วนที่เหมาะสมที่ทำให้เกิดจำนวนคละ
ในจำนวนคละ \(3\frac{1}{2}\)
ขั้นตอนที่ 1: หารตัวเศษด้วยตัวส่วน
ขั้นตอนที่ 2: จดผลหารเป็นจำนวนเต็ม
ขั้นตอนที่ 3: เขียนเศษที่เหลือเป็นตัวเศษและตัวหารเป็นตัวส่วน
ตัวอย่างเช่น เราทำตามขั้นตอนที่กำหนดเพื่อแปลง \(\frac{7}{3}\) เป็นรูปแบบจำนวนคละ
ขั้นตอนที่ 1: หาร 7 ด้วย 3
ขั้นตอนที่ 2: เขียนผลหาร ตัวหาร และเศษเหลือในรูปแบบจำนวนคละ: \(2\frac{1}{3}\)
เราสามารถบวก (หรือลบ) จำนวนคละได้โดยการจัดเรียงจำนวนเต็มใหม่ บวก (หรือลบ) แยกจากกัน และบวกเศษส่วนที่เหลือทีละส่วนและรวมเข้าด้วยกันในตอนท้าย
\(1\frac{1}{2} + 3\frac{3}{4} \)
การบวกจำนวนเต็มแยกกันและเศษส่วนแยกกัน
สำหรับจำนวนเต็ม:
1 + 3 = 4
สำหรับเศษส่วน: ค้นหา LCM แล้วบวก
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
การแปลงเศษเกินเป็นจำนวนคละ: \(\frac{5}{4} = 1\frac{1}{4}\)
ในตอนท้ายให้เพิ่มทั้งสองส่วนเข้าด้วยกัน
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
เพียงทำตามวิธีเดียวกัน (เช่นการบวก) แต่ลบแทนการบวก:
ตัวอย่าง: \(15\frac{3}{4} - 8\frac{5}{6}\)
แปลงเป็นเศษเกิน: \(\frac{63}{4} - \frac{53}{6}\)
ตัวส่วนร่วม (LCM ของ 4 และ 6) ของ 12: \(\frac{189}{12} - \frac{106}{12}\)
ตอนนี้ลบ: \(\frac{83}{12}\)
เปลี่ยนเป็นเศษส่วนคละ: \(6\frac{11}{12}\)
ตัวอย่าง: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
ตัวอย่าง:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)