Back to the topics list

karışık kesir, karışık sayılar

Karışık kesirler nelerdir?

Karışık bir kesir bir tam sayıdır ve uygun bir kesir birlikte temsil edilir. Genellikle herhangi iki tam sayı arasındaki bir sayıyı temsil eder.

Karışık kesirler aynı zamanda karışık sayılar olarak da bilinir.

Verilen resme bakın, 1'den büyük ancak 2'den küçük bir kesri temsil ediyor. Bu nedenle, \(1\frac{3}{4}\) e eşit bir karışık sayıdır.

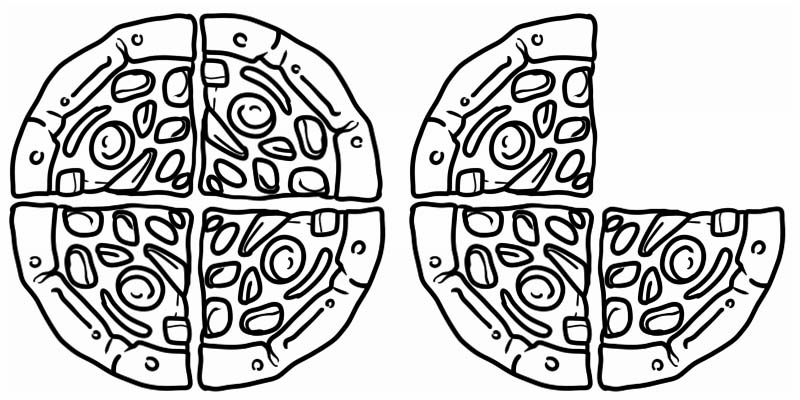
Karışık sayıların diğer bazı örnekleri şunlardır:

\(3\frac{1}{2}\)

\(2\frac{3}{5}\)

\(5\frac{3}{5}\)

\(4\frac{1}{5}\)

Karışık bir sayının parçaları

Üç parçanın birleştirilmesiyle karışık bir sayı oluşturulur: bir tam sayı, bir pay ve bir payda. Pay ve payda, karışık sayıyı oluşturan uygun kesrin bir parçasıdır.

\(3\frac{1}{2}\) karışık sayısında

• 3 tam sayıdır
• \(\frac{1}{2}\) , 1'in pay ve 2'nin payda olduğu bir kesirdir

karışık sayıların özellikleri

• kısmen bir tam sayıdır
• kısmen bir kesirdir

Uygun olmayan kesri karışık kesre dönüştürme

Adım 1: Payı paydaya bölün

Adım 2: Bölümü tam sayı olarak yazın

Adım 3: Pay olarak kalanı ve payda olarak böleni yazın

Örneğin, \(\frac{7}{3}\) öğesini karma sayı biçimine dönüştürmek için verilen adımları takip ediyoruz.

1. Adım: 7'yi 3'e bölün

Adım 2: Bölüm, bölen ve kalanı karışık sayı biçiminde yazın: \(2\frac{1}{3}\)

Karışık kesirleri toplama veya çıkarma

Tam sayıları yeniden düzenleyerek, ayrı ayrı toplayarak (veya çıkararak) ve kalan kesirleri tek tek ekleyerek ve sonunda hepsini birleştirerek karışık sayılar toplanabilir (veya çıkarılabilir).

\(1\frac{1}{2} + 3\frac{3}{4} \)

Tam sayıları ayrı ayrı, kesirleri ayrı ayrı toplama.

tam sayılar için:

1 + 3 = 4

Kesirler için: LCM'yi bulun ve ardından ekleyin

\(\frac{1}{2} + \frac{3}{4}\)

= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)

= \(\frac{2}{4} + \frac{3}{4}\)

= \(\frac{5}{4}\)

Yanlış kesri karışık sayıya dönüştürme: \(\frac{5}{4} = 1\frac{1}{4}\)

Sonunda, her iki parçayı bir araya getirmek.

\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)

Karışık kesirleri çıkarma

Sadece aynı yöntemi uygulayın (toplamak için olduğu gibi), ancak eklemek yerine çıkarın:

Örnek: \(15\frac{3}{4} - 8\frac{5}{6}\)

Uygunsuz kesirlere dönüştürün: \(\frac{63}{4} - \frac{53}{6}\)

12'nin ortak paydası (4 ve 6'nın LCM'si): \(\frac{189}{12} - \frac{106}{12}\)

Şimdi çıkarın: \(\frac{83}{12}\)

Karışık bir kesre dönüştürün: \(6\frac{11}{12}\)

Karışık Kesirleri Çarpma

• Her karışık kesri uygun olmayan bir kesre değiştirin
• Mümkünse basitleştirin
• Payları ve ardından paydaları çarpın
• Cevabı en düşük terimlerle yazın
• Cevabın anlamlı olduğundan emin olmak için kontrol edin

Örnek: \(5\frac{2}{3} \times \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{1}{4}\)

= \(\frac{17}{12}\)

= \(1\frac{5}{12}\)

Karışık kesirleri bölme

• Her karışık kesri uygun olmayan bir kesre değiştirin
• Mümkünse sadeleştirerek bölenin tersi ile çarpın
• Cevabı en düşük terimlerle yazın
• Cevabın anlamlı olduğundan emin olmak için kontrol edin

Örnek:

\(5\frac{2}{3} \div \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{4}{1}\)

= \(\frac{68}{3}\)

= \(22\frac{2}{3}\)