Змішаний дріб - це ціле число, а правильний дріб представлені разом. Зазвичай це число між будь-якими двома цілими числами.
Змішані дроби також називають змішаними числами.
Подивіться на дане зображення, воно представляє дріб, більший за 1, але менший за 2. Таким чином, це змішане число, яке дорівнює \(1\frac{3}{4}\)
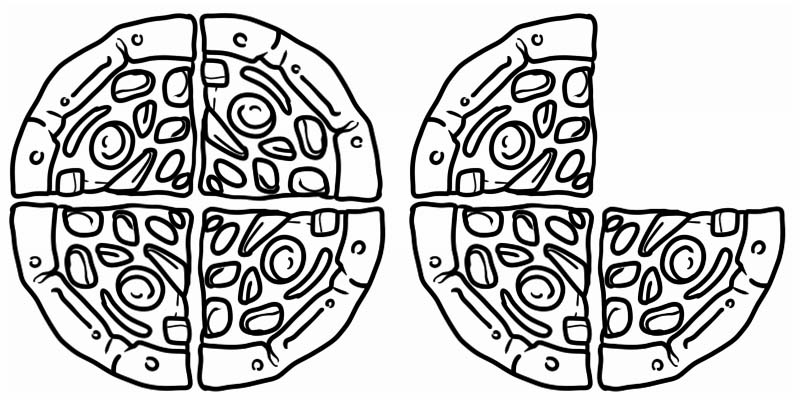
Деякі інші приклади змішаних чисел:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Мішане число утворюється об’єднанням трьох частин: цілого числа, чисельника та знаменника. Чисельник і знаменник є частиною правильного дробу, який утворює мішане число.
У змішаному числі \(3\frac{1}{2}\)
Крок 1: Розділіть чисельник на знаменник
Крок 2. Запишіть частку як ціле число
Крок 3. Запишіть остачу як чисельник, а дільник — як знаменник
Наприклад, ми виконуємо наведені кроки, щоб перетворити \(\frac{7}{3}\) у форму змішаного числа.
Крок 1: розділіть 7 на 3
Крок 2. Запишіть частку, дільник і залишок у формі змішаного числа: \(2\frac{1}{3}\)
Можна додавати (або віднімати) змішані числа, переставляючи цілі числа, додаючи (або віднімаючи) їх окремо та додаючи залишені дроби окремо та, нарешті, об’єднуючи їх усі.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Додавання окремо цілих чисел і окремо дробів.
Для цілих чисел:
1 + 3 = 4
Для дробів: знайдіть НКР і додайте
\(\frac{1}{2} + \frac{3}{4}\)
\(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Перетворення неправильного дробу на змішане число: \(\frac{5}{4} = 1\frac{1}{4}\)
Зрештою, складіть обидві частини разом.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Просто виконайте той самий метод (як для додавання), але віднімайте замість додавання:
Приклад: \(15\frac{3}{4} - 8\frac{5}{6}\)
Перетворення на неправильні дроби: \(\frac{63}{4} - \frac{53}{6}\)
Загальний знаменник (LCM 4 і 6) 12: \(\frac{189}{12} - \frac{106}{12}\)
Тепер відніміть: \(\frac{83}{12}\)
Перетворіть на змішаний дріб: \(6\frac{11}{12}\)
Приклад: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
приклад:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)