Back to the topics list

aralash fraksiya, aralash raqamlar

Aralash kasrlar nima?

Aralash kasr butun son va birgalikda ifodalangan to'g'ri kasrdir. Odatda u har qanday ikkita butun son orasidagi sonni ifodalaydi.

Aralash kasrlar aralash sonlar deb ham ataladi.

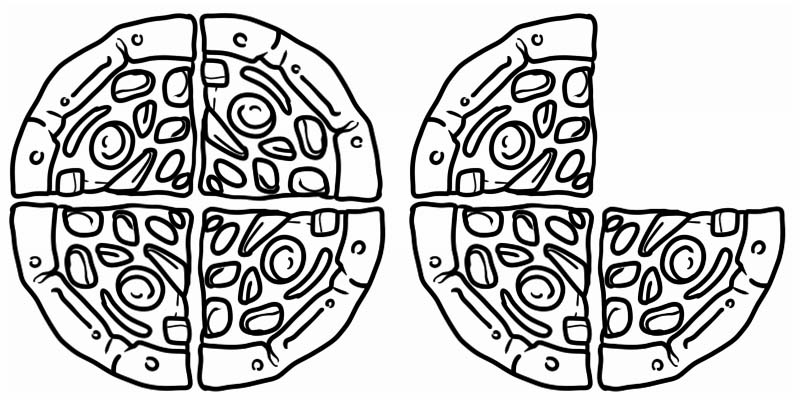
Berilgan rasmga qarang, u 1 dan katta, lekin 2 dan kichik kasrni ifodalaydi. Shunday qilib, u \(1\frac{3}{4}\) ga teng aralash sondir.

Boshqa aralash raqamlarga misollar:

\(3\frac{1}{2}\)

\(2\frac{3}{5}\)

\(5\frac{3}{5}\)

\(4\frac{1}{5}\)

Aralash sonning qismlari

Aralash son uch qismni: butun son, ayiruvchi va maxrajni birlashtirish orqali hosil bo'ladi. Numerator va maxraj aralash sonni hosil qiluvchi to'g'ri kasrning bir qismidir.

Aralash sonda \(3\frac{1}{2}\)

• 3 - butun son
• \(\frac{1}{2}\) - kasr, bu erda 1 - ayiruvchi va 2 - maxraj.

Aralash sonlarning xossalari

• Bu qisman butun sondir
• Bu qisman kasr

Noto'g'ri kasrni aralash kasrga aylantirish

1-qadam: Numeratorni maxrajga bo'ling

2-qadam: qismni butun son sifatida yozing

3-qadam: Qolganni ayiruvchi va boʻluvchini maxraj sifatida yozing.

Masalan, \(\frac{7}{3}\) aralash son shakliga aylantirish uchun berilgan amallarni bajaramiz.

1-qadam: 7 ni 3 ga bo'ling

2-qadam: Bo'linuvchi, bo'linuvchi va qoldiqni aralash sonlar ko'rinishida yozing: \(2\frac{1}{3}\)

Aralash kasrlarni qo'shish yoki ayirish

Aralash raqamlarni butun sonlarni qayta tartiblash, ularni alohida qo'shish (yoki ayirish) va qolgan kasrlarni alohida qo'shish va oxirida hammasini birlashtirish orqali qo'shish (yoki ayirish) mumkin.

\(1\frac{1}{2} + 3\frac{3}{4} \)

Butun sonlarni alohida va kasrlarni alohida qo'shish.

Butun sonlar uchun:

1 + 3 = 4

Kasrlar uchun: LCM ni toping va keyin qo'shing

\(\frac{1}{2} + \frac{3}{4}\)

= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)

= \(\frac{2}{4} + \frac{3}{4}\)

= \(\frac{5}{4}\)

Noto'g'ri kasrni aralash songa aylantirish: \(\frac{5}{4} = 1\frac{1}{4}\)

Oxirida ikkala qismni bir-biriga qo'shing.

\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)

Aralash kasrlarni ayirish

Xuddi shu usulga amal qiling (qo'shish kabi), lekin qo'shish o'rniga ayirib tashlang:

Misol: \(15\frac{3}{4} - 8\frac{5}{6}\)

Noto'g'ri kasrlarga aylantiring: \(\frac{63}{4} - \frac{53}{6}\)

Umumiy maxraj (LCM 4 va 6) 12: \(\frac{189}{12} - \frac{106}{12}\)

Endi ayiring: \(\frac{83}{12}\)

Aralash kasrga o'zgartirish: \(6\frac{11}{12}\)

Aralash kasrlarni ko'paytirish

• Har bir aralash kasrni noto'g'ri kasrga o'zgartiring
• Iloji bo'lsa, soddalashtiring
• Numeratorlarni, keyin esa maxrajlarni ko'paytiring
• Javobni eng past shartlarda qo'ying
• Javob mantiqiy ekanligiga ishonch hosil qiling

Misol: \(5\frac{2}{3} \times \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{1}{4}\)

= \(\frac{17}{12}\)

= \(1\frac{5}{12}\)

Aralash kasrlarni bo'lish

• Har bir aralash kasrni noto'g'ri kasrga o'zgartiring
• Bo'luvchining o'zaro nisbatiga ko'paytiring, iloji bo'lsa soddalashtiring
• Javobni eng past shartlarda qo'ying
• Javob mantiqiy ekanligiga ishonch hosil qiling

Misol:

\(5\frac{2}{3} \div \frac{1}{4}\)

= \(\frac{17}{3} \times \frac{4}{1}\)

= \(\frac{68}{3}\)

= \(22\frac{2}{3}\)