Một phân số hỗn hợp là một số nguyên và một phân số thích hợp được biểu diễn cùng nhau. Nó thường đại diện cho một số nằm giữa hai số nguyên bất kỳ.
Hỗn số còn được gọi là hỗn số.
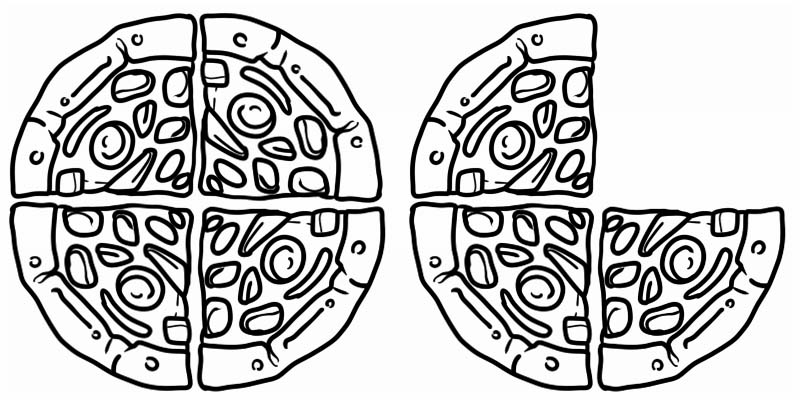
Nhìn vào hình ảnh đã cho, nó đại diện cho một phân số lớn hơn 1 nhưng nhỏ hơn 2. Do đó, nó là một hỗn số, bằng \(1\frac{3}{4}\)
Một số ví dụ khác về hỗn số là:
\(3\frac{1}{2}\)
\(2\frac{3}{5}\)
\(5\frac{3}{5}\)
\(4\frac{1}{5}\)
Một hỗn số được hình thành bằng cách kết hợp ba phần: một số nguyên, một tử số và một mẫu số. Tử số và mẫu số là một phần của phân số thích hợp tạo nên hỗn số.
Trong hỗn số \(3\frac{1}{2}\)
Bước 1: Chia tử số cho mẫu số
Bước 2: Viết thương dưới dạng số nguyên
Bước 3: Lấy số dư làm tử số, lấy số chia làm mẫu số
Ví dụ: chúng tôi làm theo các bước đã cho để chuyển đổi \(\frac{7}{3}\) thành dạng hỗn số.
Bước 1: Chia 7 cho 3
Bước 2: Viết thương, số chia và số dư ở dạng hỗn số: \(2\frac{1}{3}\)
Người ta có thể cộng (hoặc trừ) các hỗn số bằng cách sắp xếp lại các số nguyên, cộng (hoặc trừ) chúng một cách riêng biệt và cộng các phân số còn lại riêng lẻ và cuối cùng kết hợp tất cả chúng.
\(1\frac{1}{2} + 3\frac{3}{4} \)
Cộng riêng các số nguyên và các phân số riêng.
Đối với các số nguyên:
1 + 3 = 4
Đối với phân số: Tìm LCM rồi cộng
\(\frac{1}{2} + \frac{3}{4}\)
= \(\frac{1}{2} \times \frac{2}{2} + \frac{3}{4}\)
= \(\frac{2}{4} + \frac{3}{4}\)
= \(\frac{5}{4}\)
Chuyển phân số không chính xác thành hỗn số: \(\frac{5}{4} = 1\frac{1}{4}\)
Cuối cùng, thêm cả hai phần lại với nhau.
\(4+ 1\frac{1}{4} = 5\frac{1}{4}\)
Chỉ cần làm theo cùng một phương pháp (như để thêm), nhưng trừ thay vì thêm:
Ví dụ: \(15\frac{3}{4} - 8\frac{5}{6}\)
Chuyển đổi thành phân số không chính xác: \(\frac{63}{4} - \frac{53}{6}\)
Mẫu số chung (LCM của 4 và 6) của 12: \(\frac{189}{12} - \frac{106}{12}\)
Bây giờ hãy trừ: \(\frac{83}{12}\)
Đổi thành hỗn số: \(6\frac{11}{12}\)
Ví dụ: \(5\frac{2}{3} \times \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{1}{4}\)
= \(\frac{17}{12}\)
= \(1\frac{5}{12}\)
Ví dụ:
\(5\frac{2}{3} \div \frac{1}{4}\)
= \(\frac{17}{3} \times \frac{4}{1}\)
= \(\frac{68}{3}\)
= \(22\frac{2}{3}\)