Што ќе научиме: Користење на методот на долга поделба за делење големи броеви
За да делите големи броеви користете го методот на долга поделба. За разлика од другите аритметички операции, долгата поделба се движи од лево кон десно, што значи дека операцијата за делење започнува од најлевата цифра. Долгиот повеќецифрен број се дели на мали задачи за делење со помош на овој метод.
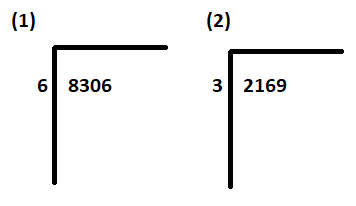
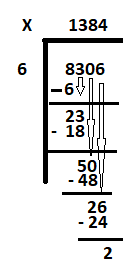
Чекор 1: Напишете дивиденда (8306, 2169) во симболот за поделба на десната страна. Напишете делител(6, 3) надвор од симболот за поделба на левата страна.
Чекор 2: Во случајот 1, започнете со првата цифра од левата страна на дивидендата 8306. Тоа е 8. Откријте колку 6 е еднакво или речиси еднакво на 8 или со други зборови колку 6 се вклопува во 8. Одговорот е 1. Затоа 6 по 1 е 6. Одземете 6 од 8 за да го добиете остатокот како 2. Намалете ја следната цифра „3“ за да ја направите новата дивиденда како 23.
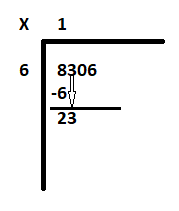
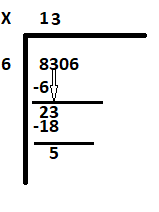
Чекор 3: Откријте колку 6 е еднакво на 23. 6 три пати е 18. Запишете 3 до 1 и одземете 18 од 23 за да го добиете остатокот како 5.
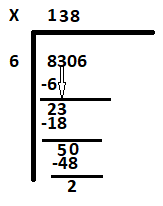
спуштете го 0 за да ја добиете следната дивиденда како 50. Колку 6 се вклопуваат во 50. Одговорот е 8. Запишете 8 до 3 и одземете 48 од 50. Остатокот е 2.
Чекор 4: Намалете ја последната цифра 6, за да ја добиете следната дивиденда како 26. Колку 6 е скоро еднакво на 26? Одговорот е 4. Запишете 4 до 8 и одземете 24 од 26 за да го добиете остатокот како 2
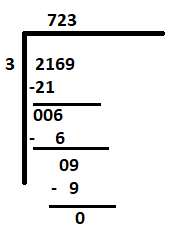
Ајде да се обидеме да го решиме вториот проблем- 2169 ÷ 3
Бидејќи најлевата цифра е 2, што е помало од делителот 3, затоа земете го „21“ како прва дивиденда. Останатите чекори ќе бидат исти како погоре.
Забелешка: Наместо делење една цифра во исто време, можеме да земеме голем дел од цифри од дивидендата. Можеме да одиме 2 или 3 цифри истовремено, ова ќе ги намали чекорите на поделба.