Wat we zullen leren: De staartdelingsmethode gebruiken om grote getallen te delen
Gebruik de staartdelingsmethode om grote getallen te delen. In tegenstelling tot andere rekenkundige bewerkingen, beweegt staartdeling van links naar rechts, wat betekent dat de deling begint vanaf het meest linkse cijfer. Het lange meercijferige getal wordt met deze methode opgedeeld in kleine deelproblemen.
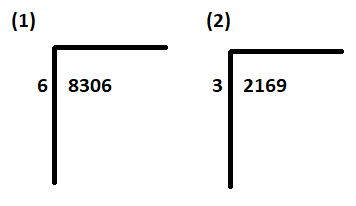
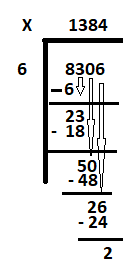
Stap 1: schrijf dividend (8306, 2169) in het delingssymbool aan de rechterkant. Schrijf deler(6, 3) buiten het delingssymbool aan de linkerkant.
Stap 2: Begin in geval 1 met het eerste cijfer aan de linkerkant van het deeltal 8306. Het is 8. Zoek uit hoeveel 6 gelijk is aan of bijna gelijk is aan 8 of met andere woorden hoeveel 6 in 8 past. Het antwoord is 1. Daarom is 6 keer 1 6. Trek 6 af van 8 om de rest te krijgen als 2. Breng het volgende cijfer '3' naar beneden om het nieuwe deeltal te maken als 23.
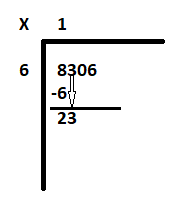
Stap 3: Zoek uit hoeveel 6 gelijk is aan 23. 6 drie keer is 18. Schrijf 3 naast 1 en trek 18 af van 23 om de rest als 5 te krijgen.
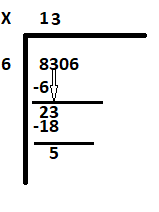
verlaag 0 om het volgende deeltal te krijgen als 50. Hoeveel 6 passen in 50. Het antwoord is 8. Schrijf 8 naast 3 en trek 48 af van 50. De rest is 2.
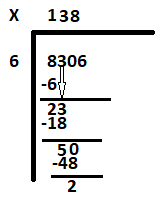
Stap 4: Verlaag het laatste cijfer 6 om het volgende deeltal 26 te krijgen. Hoeveel 6 is bijna gelijk aan 26? Het antwoord is 4. Schrijf 4 naast 8 en trek 24 af van 26 om de rest als 2 te krijgen
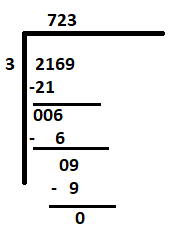
Laten we proberen het tweede probleem op te lossen: 2169 ÷ 3
Aangezien het meest linkse cijfer 2 is, wat kleiner is dan de deler 3, beschouw '21' daarom als het eerste deeltal. De rest van de stappen zijn hetzelfde als hierboven.
Opmerking: in plaats van één cijfer tegelijk te delen, kunnen we een groot aantal cijfers van het deeltal nemen. We kunnen 2 of 3 cijfers tegelijk gaan, dit vermindert de delingsstappen.