Czego się nauczymy: Używanie metody dzielenia długiego do dzielenia dużych liczb
Aby podzielić duże liczby, użyj metody dzielenia długiego. W przeciwieństwie do innych operacji arytmetycznych, dzielenie długie przesuwa się od lewej do prawej, co oznacza, że operacja dzielenia rozpoczyna się od skrajnej lewej cyfry. Długa liczba wielocyfrowa jest dzielona na małe problemy dzielenia przy użyciu tej metody.
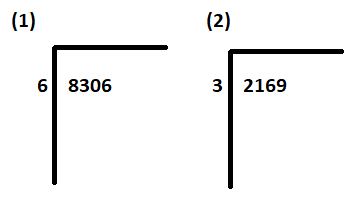
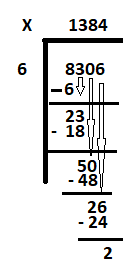
Krok 1: Napisz dywidendę (8306, 2169) wewnątrz symbolu dzielenia po prawej stronie. Zapisz dzielnik(6, 3) poza symbolem dzielenia po lewej stronie.
Krok 2: W przypadku 1 zacznij od pierwszej cyfry od lewej strony dzielnej 8306. Jest to 8. Dowiedz się, ile 6 jest równe lub prawie równe 8, czyli innymi słowy, ile 6 mieści się w 8. Odpowiedź to 1. Zatem 6 razy 1 daje 6. Odejmij 6 od 8, aby otrzymać resztę jako 2. Zmniejsz następną cyfrę „3”, aby nowa dzielna wyniosła 23.
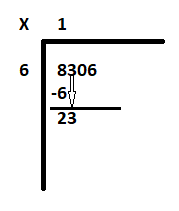
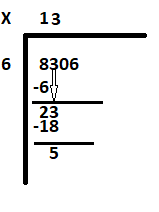
Krok 3: Dowiedz się, ile 6 równa się 23. 6 trzy razy to 18. Wpisz 3 obok 1 i odejmij 18 od 23, aby otrzymać resztę jako 5.
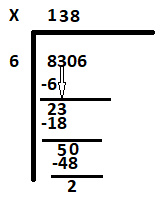
obniż 0, aby otrzymać następną dywidendę jako 50. Ile 6 mieści się w 50. Odpowiedź to 8. Wpisz 8 obok 3 i odejmij 48 od 50. Reszta to 2.
Krok 4: Zmniejsz ostatnią cyfrę 6, aby otrzymać następną dywidendę jako 26. Ile 6 jest prawie równe 26? Odpowiedź to 4. Wpisz 4 obok 8 i odejmij 24 od 26, aby otrzymać resztę jako 2
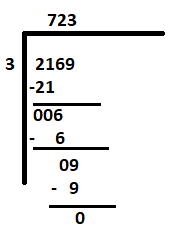
Spróbujmy rozwiązać drugi problem - 2169 ÷ 3
Ponieważ najbardziej wysunięta na lewo cyfra to 2, czyli mniej niż dzielnik 3, dlatego pierwszą dywidendę należy uznać za „21”. Pozostałe kroki będą takie same jak powyżej.
Uwaga: zamiast dzielenia jednej cyfry na raz możemy wziąć dużą część cyfr dywidendy. Możemy przejść 2 lub 3 cyfry na raz, zmniejszy to kroki dzielenia.