Что мы будем изучать: Использование метода деления в длину для деления больших чисел.
Для деления больших чисел используйте метод деления в длину. В отличие от других арифметических операций, длинное деление выполняется слева направо, что означает, что операция деления начинается с самой левой цифры. С помощью этого метода длинное многозначное число разбивается на мелкие задачи деления.
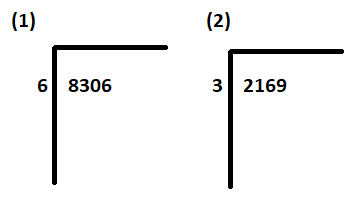
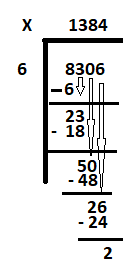
Шаг 1: Напишите делимое (8306, 2169) внутри символа деления справа. Напишите divisor(6, 3) вне символа деления слева.
Шаг 2: В случае 1 начните с первой цифры слева от делимого 8306. Это 8. Выясните, сколько 6 равно или почти равно 8 или, другими словами, сколько 6 укладывается в 8. Ответ равно 1. Следовательно, 6 умножить на 1 равно 6. Вычтите 6 из 8, чтобы получить остаток как 2. Сократите следующую цифру «3», чтобы новое делимое стало равным 23.
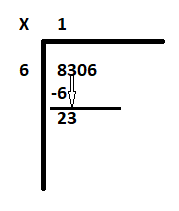
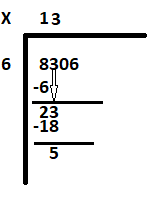
Шаг 3: Узнайте, сколько 6 равно 23. 6, умноженное на три, равно 18. Напишите 3 рядом с 1 и вычтите 18 из 23, чтобы получить в остатке 5.
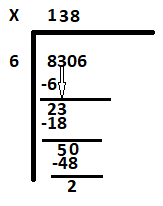
уменьшите 0, чтобы получить следующее делимое как 50. Сколько 6 помещается в 50. Ответ: 8. Напишите 8 рядом с 3 и вычтите 48 из 50. Остаток равен 2.
Шаг 4: Сократите последнюю цифру 6, чтобы получить следующее делимое как 26. Сколько 6 почти равно 26? Ответ: 4. Напишите 4 рядом с 8 и вычтите 24 из 26, чтобы получить в остатке 2.
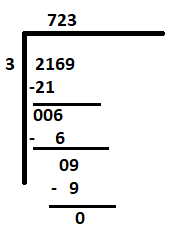
Попробуем решить вторую задачу- 2169 ÷ 3
Поскольку крайняя левая цифра равна 2, что меньше делителя на 3, поэтому считайте «21» первым делимым. Остальные шаги будут такими же, как описано выше.
Примечание. Вместо деления по одной цифре мы можем взять большой кусок цифр делимого. Мы можем идти по 2 или 3 цифры за раз, это уменьшит шаги деления.