Vad vi kommer att lära oss: Att använda den långa divisionsmetoden för att dividera stora tal
För att dela stora tal använd den långa divisionsmetoden. Till skillnad från andra aritmetiska operationer, flyttar lång division från vänster till höger, vilket innebär att divisionsoperationen börjar från siffran längst till vänster. Det långa flersiffriga numret delas upp i små divisionsproblem med denna metod.
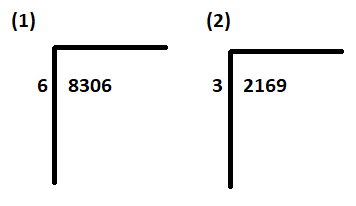
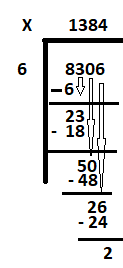
Steg 1: Skriv utdelning (8306, 2169) inuti divisionssymbolen på höger sida. Skriv divisor(6, 3) utanför divisionssymbolen på vänster sida.
Steg 2: I fall 1, börja med den första siffran från vänster sida av utdelningen 8306. Det är 8. Ta reda på hur många 6 är lika med eller nästan lika med 8 eller med andra ord hur många 6 som passar in i 8. Svaret är 1. Därför är 6 gånger 1 6. Subtrahera 6 från 8 för att få resten som 2. Dra ner nästa siffra '3' för att få den nya utdelningen till 23.
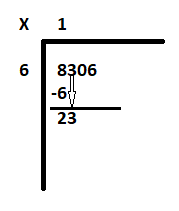
Steg 3: Ta reda på hur många 6 är lika med 23. 6 tre gånger är 18. Skriv 3 bredvid 1 och subtrahera 18 från 23 för att få resten som 5.
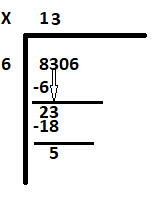
få ner 0 för att få nästa utdelning som 50. Hur många 6 passar i 50. Svaret är 8. Skriv 8 bredvid 3 och subtrahera 48 från 50. Resten är 2.
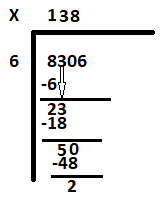
Steg 4: Ta ner den sista siffran 6, för att få nästa utdelning som 26. Hur många 6 är nästan lika med 26? Svaret är 4. Skriv 4 bredvid 8 och subtrahera 24 från 26 för att få resten som 2
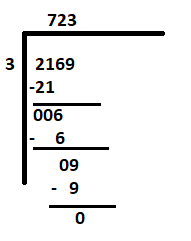
Låt oss försöka lösa det andra problemet - 2169 ÷ 3
Eftersom siffran längst till vänster är 2, vilket är mindre än divisor 3, betrakta därför "21" som den första utdelningen. Resten av stegen kommer att vara desamma som ovan.
Notera: I stället för att dividera en siffra i taget kan vi ta en stor del av siffrorna av utdelningen. Vi kan gå 2 eller 3 siffror åt gången, detta kommer att minska divisionsstegen.