สิ่งที่เราจะได้เรียนรู้: การใช้วิธีหารยาวเพื่อหารจำนวนมาก
การหารจำนวนมากใช้วิธีหารยาว ซึ่งแตกต่างจากการดำเนินการทางคณิตศาสตร์อื่น ๆ การหารยาวจะย้ายจากซ้ายไปขวา ซึ่งหมายความว่าการดำเนินการหารจะเริ่มต้นจากหลักซ้ายสุด ตัวเลขหลายหลักที่ยาวถูกแบ่งออกเป็นปัญหาการหารย่อยโดยใช้วิธีนี้
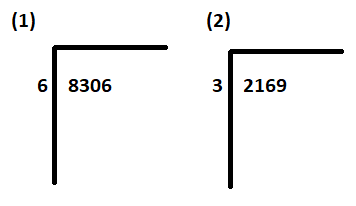
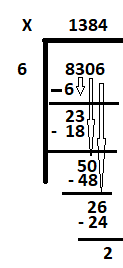
ขั้นตอนที่ 1: เขียน เงินปันผล (8306, 2169) ภายในสัญลักษณ์หารทางด้านขวา เขียนตัวหาร (6, 3) นอกสัญลักษณ์หารทางด้านซ้าย
ขั้นตอนที่ 2: กรณีที่ 1 ให้เริ่มด้วยหลักแรกทางด้านซ้ายของเงินปันผล 8306 ซึ่งก็คือ 8 จงหาว่า 6 เท่ากับหรือเกือบเท่ากับ 8 กี่ตัว หรืออีกนัยหนึ่งคือจำนวน 6 หารด้วย 8 ได้กี่ตัว คำตอบ คือ 1 ดังนั้น 6 คูณ 1 ได้ 6 ลบ 6 จาก 8 เพื่อให้ได้เศษเหลือเป็น 2 นำตัวเลขถัดไป '3' ลงเพื่อสร้างเงินปันผลใหม่เป็น 23
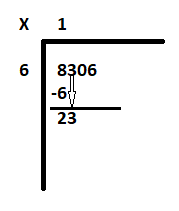
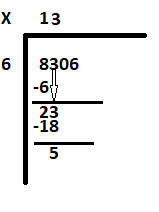
ขั้นตอนที่ 3: หาจำนวน 6 เท่ากับ 23 6 สามครั้งได้ 18 เขียน 3 ถัดจาก 1 แล้วลบ 18 จาก 23 เพื่อให้ได้เศษเหลือเป็น 5
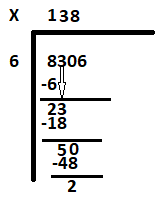
นำ 0 ลงมาเพื่อรับเงินปันผลถัดไปเป็น 50 มี 6 กี่ตัวใน 50 คำตอบคือ 8 เขียน 8 ถัดจาก 3 และลบ 48 จาก 50 ส่วนที่เหลือคือ 2
ขั้นตอนที่ 4: นำ 6 หลักสุดท้ายลงมาเพื่อรับเงินปันผลถัดไปเป็น 26 6 เกือบเท่ากับ 26 มีกี่ตัว คำตอบคือ 4 เขียน 4 ถัดจาก 8 และลบ 24 จาก 26 เพื่อให้ได้เศษเหลือเป็น 2
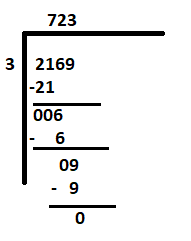
ลองแก้ปัญหาที่สองกัน - 2169 ÷ 3
เนื่องจากหลักซ้ายสุดคือ 2 ซึ่งน้อยกว่าตัวหาร 3 ดังนั้นให้ถือว่า '21' เป็นเงินปันผลตัวแรก ขั้นตอนที่เหลือจะเหมือนกับข้างต้น
หมายเหตุ: แทนที่จะแบ่งทีละหลัก เราสามารถนำหลักจำนวนมากของเงินปันผลมาหารได้ เราสามารถไปทีละ 2 หรือ 3 หลัก ซึ่งจะช่วยลดขั้นตอนการหาร