الكسر هو جزء من الكل. الكائن الكامل أو الكامل هو الكل. يمكن أن يكون الكل مجموعة من الأشياء أو كائنًا واحدًا. عندما نقسم كل شيء إلى أجزاء متساوية ، فإن كل جزء يسمى كسر.
في الصورة أدناه ، يتم تقسيم تفاحة كاملة إلى نصفين. كل نصف هو كسر يتم تمثيله كـ \(\frac{1}{2}\) حيث يمثل 1 البسط و 2 هو المقام.

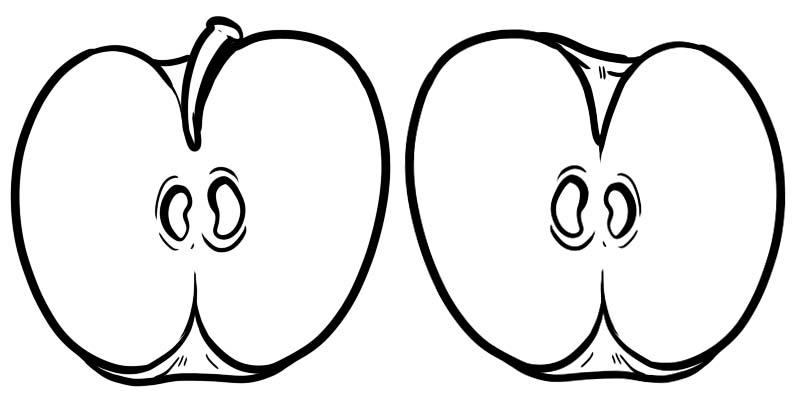
يتكون الكسر من رقمين مقسومين على خط.
يُعرف الرقم المكتوب أسفل الخط بالمقام. المقام يوضح عدد الأجزاء المتساوية التي تم تقسيم شيء ما إليها.
يُعرف الرقم المكتوب فوق الخط بالبسط. يوضح البسط عدد أجزاء الكل المأخوذة.
يمكن أن يكون البسط أكبر أو أصغر من المقام.
المقام لا يساوي صفرًا أو واحدًا.
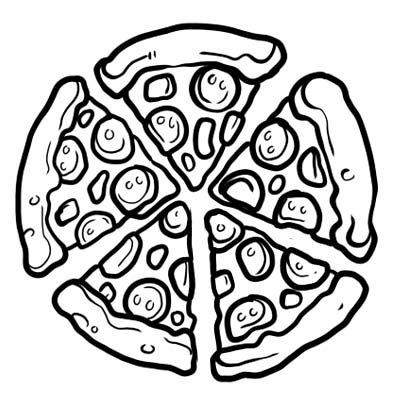
تنقسم البيتزا إلى خمسة أجزاء متساوية. إذا كنت تأكل شريحة واحدة فقط من البيتزا ، فهذا يعني أنك أكلت \(\frac{1}{5}\) من البيتزا بأكملها. \(\frac{1}{5}\) هو الكسر الموجود هنا.
أنصاف وأرباع
كان هاري وجاك جائعين. اشتروا كب كيك. تقاسموا الكب كيك بتقسيمه إلى قسمين متساويين:

هنا ، الجزء 1 والجزء 2 جزءان من الكب كيك. الجزء الأول هو النصف والجزء الثاني هو النصف الآخر.
الأرباع (1/4) وثلاثة أرباع (3/4)
اشترى هاري وجاك وسام وأوليفر قطعة من الشوكولاتة. قطعوها إلى 4 أجزاء متساوية.
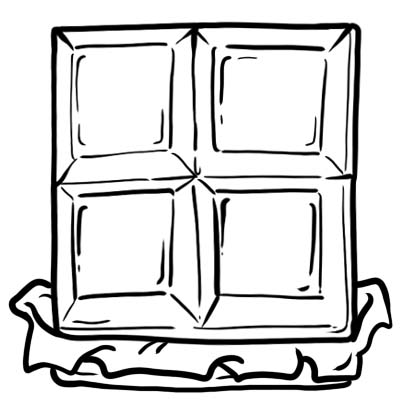
كل جزء أو مكعب من الشوكولاتة هو ربع أي \(\frac{1}{4}\)
هذا يعني أن حبة شوكولاتة كاملة مقسمة إلى أربعة أجزاء متساوية.
لنفترض أن جاك أكل الجزء الخاص به من الشوكولاتة ، يمكننا القول إنه أكل ربع أو \(\frac{1}{4}\) من الشوكولاتة. كم تبقى من الشوكولاتة الآن؟ بقي 3 أجزاء ، لذلك يمكننا القول أن \(\frac{3}{4}\) أو ثلاثة أرباع الشوكولاتة متبقية.
ألق نظرة على الشكل الموضح أدناه ،
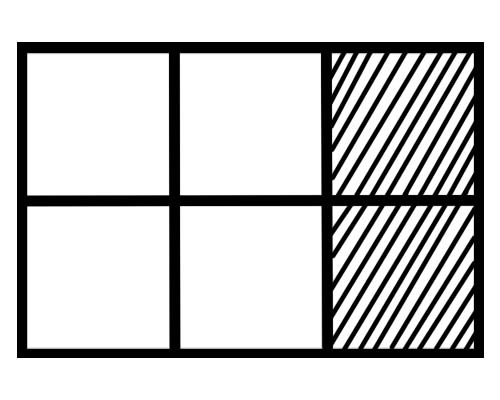
ما هو كسر كل جزء في هذا الشكل؟ هناك ستة أجزاء متساوية ، لذا فإن كسر كل جزء هو \(\frac{1}{6}\) .
كم عدد أجزاء الكل المظللة في الشكل المعطى؟ جزءان من الأجزاء الستة الإجمالية مظللة ، لذا فإن الكسر الإجمالي هو \(\frac{2}{6}\) .
كم عدد أجزاء الكل غير المظللة في الشكل المعطى؟ 4 أجزاء من مجموع 6 أجزاء غير مظللة ، لذا فإن الكسر الكلي هو \(\frac{4}{6}\) .
يمكننا أيضًا استخدام كسر لتمثيل جزء من مجموعة. لنأخذ مثالاً على فصل يضم 12 طالبًا ويريد مدرس الفصل تقسيم الفصل إلى مجموعتين متساويتين. سيكون لكل مجموعة 6 طلاب. \(\frac{1}{2}\) من 12 يساوي 6 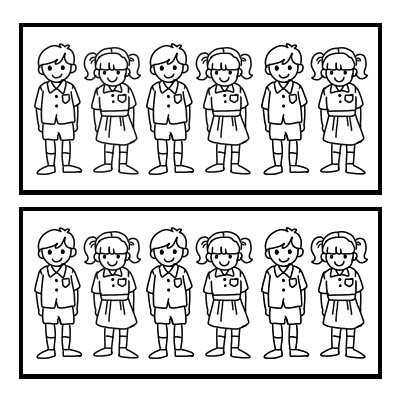
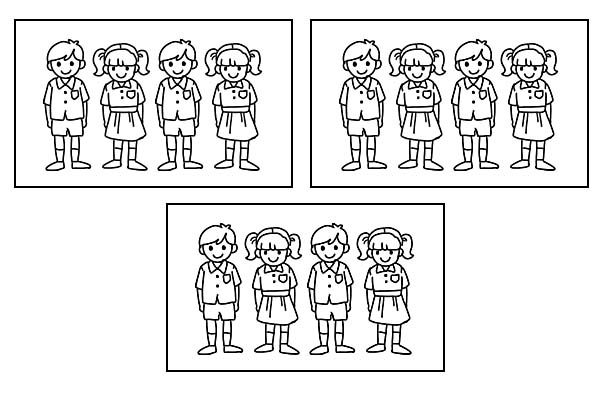
إذا تم تقسيم نفس الفصل إلى 3 مجموعات متساوية ، فسيكون لكل مجموعة 4 طلاب. كـ \(\frac{1}{3}\) من 12 يساوي 4.
هناك أنواع مختلفة من الكسور كما هو موضح أدناه:
الكسور الصحيحة
الكسر المناسب هو رقم يمثل جزءًا من الكل. في الكسر المناسب ، يوضح الرقم الموجود في المقام عدد الأجزاء التي يتم تقسيم الكل إليها ، بينما يوضح الرقم الموجود في البسط عدد الأجزاء التي تم أخذها. الكسر المناسب هو كسر أصغر من واحد ، حيث يكون البسط أقل من المقام.
فمثلا،
\(\frac{2}{5}\) أي جزءان من إجمالي 5 أجزاء
\(\frac{3}{7}\) أي 3 أجزاء من إجمالي 7 أجزاء
الكسور غير الصحيحة
يسمى الكسر الذي يكون فيه البسط أكبر من المقام بكسر غير فعلي.
فمثلا،
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….
كسور مختلطة
مزيج من الكل والجزء يسمى كسر مختلط.
فمثلا،
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ... إلخ.
تحويل كسر غير فعلي إلى كسر مختلط
يمكن التعبير عن الكسر غير الفعلي ككسر مختلط بقسمة البسط على مقام الكسر غير الفعلي للحصول على حاصل القسمة والباقي. ثم سيكون الكسر المختلط
الكسر المختلط = الحاصل (الباقي ∕ القاسم)
تحويل كسر مختلط إلى كسر غير فعلي
يمكن كتابة الكسر المختلط في شكل كسر غير فعلي عن طريق كتابته بالطريقة التالية:
[(كامل × المقام) + البسط)] ∕ المقام
مثل الكسور
يُقال أن الكسور التي لها نفس المقام تشبه الكسور.
فمثلا،
\(\frac{3}{10}\) و \(\frac{4}{10}\) و \(\frac{7}{10}\) مثل الكسور
على عكس الكسور
يقال إن الكسور ذات المقامات المختلفة تختلف عن الكسور.
فمثلا،
\(\frac{3}{7}\) و \(\frac{5}{9}\) و \(\frac{2}{15}\) ليست مثل الكسور
الكسور المتكافئة
يُقال أن الكسور التي تمثل نفس الجزء من الكل كسور متكافئة.
فمثلا،
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) … ..
أبسط صورة لكسر
يُقال أن الكسر في أبسط صوره أو في أدنى صوره إذا لم يكن لبسطه ومقامه عامل مشترك باستثناء واحد. يمكن أيضًا إيجاد أبسط صورة للكسر بقسمة البسط والمقام على العامل المشترك الأكبر (HCF). لنفترض ، في المثال أعلاه ، أن الكسر الأول \(\frac{1}{2}\) في أبسط صوره حيث أن 1 و 2 ليس لهما عامل مشترك باستثناء عامل واحد ؛ الكسر الثاني \(\frac{2}{4}\) ليس في أبسط صوره لأن 2 و 4 لهما عاملين مشتركين - 1 و 2 ، إذا قسمنا 2 و 4 على العامل المشترك الأكبر ، أي 2 ثم \(\frac{2}{4}\) سيصبح \(\frac{1}{2}\) وهو الآن أبسط شكل من أشكال الكسر.