Kəsr bütövün bir hissəsidir. Tam və ya tam obyekt bütövdür. Bütöv obyektlər qrupu və ya tək bir obyekt ola bilər. Bütün bir şeyi bərabər hissələrə böldükdə, hər bir hissə kəsir adlanır.
Aşağıdakı şəkildə bir tam alma iki yarıya bölünür. Hər yarım \(\frac{1}{2}\) kimi təmsil olunan kəsrdir, burada 1 ədəd, 2 isə məxrəcdir.

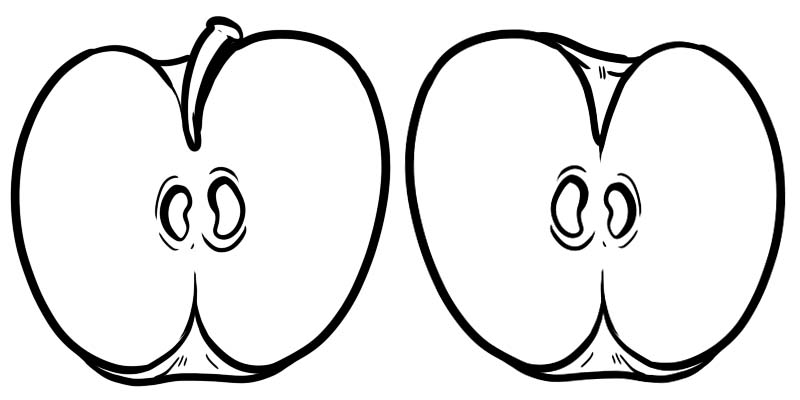
Kəsr bir xətt ilə bölünən iki ədəddən ibarətdir.
Xəttin altında yazılan rəqəm məxrəc kimi tanınır. Məxrəc bir şeyin neçə bərabər hissəyə bölündüyünü göstərir.
Xəttin üstündə yazılan nömrəyə pay deyilir. Nümerator tamın neçə hissəsinin alındığını göstərir.
Paylayıcı məxrəcdən böyük və ya kiçik ola bilər.
Məxrəc sıfıra və ya birinə bərabər DEYİL.
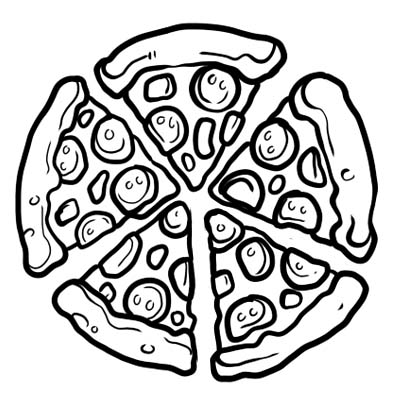
Pizza beş bərabər hissəyə bölünür. Əgər pizzadan yalnız bir dilim yeyirsinizsə, bu, bütün pizzanın \(\frac{1}{5}\) yediyiniz deməkdir. \(\frac{1}{5}\) buradakı kəsirdir.
Yarımlar və dörddəbirlər
Harri və Cek ac idilər. Kek aldılar. Keki iki bərabər hissəyə bölərək bölüşdülər:

Burada 1-ci hissə və 2-ci hissə keksin iki fraksiyasıdır. 1-ci hissə bir yarım, 2-ci hissə isə digər yarımdır.
Dörddəbir (1/4) və Dörddə Üç (3/4)
Harri, Cek, Sem və Oliver bir paket şokolad aldılar. Onu 4 bərabər hissəyə kəsdilər.
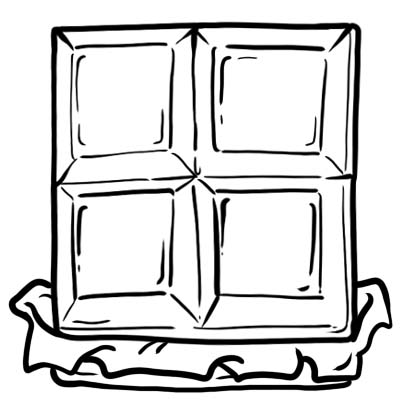
Şokoladın hər bir hissəsi və ya kubu dörddə birdir, yəni \(\frac{1}{4}\)
Bu o deməkdir ki, bir bütöv şokolad dörd bərabər hissəyə bölünür.
Tutaq ki, Cek şokoladın öz hissəsini yedi, deyə bilərik ki, o, şokoladın dörddə birini və ya \(\frac{1}{4}\) yedi. İndi nə qədər şokolad qalıb? 3 hissə qalıb, ona görə deyə bilərik ki, \(\frac{3}{4}\) və ya şokoladın dörddə üçü qalıb.
Aşağıdakı şəklə nəzər salın,
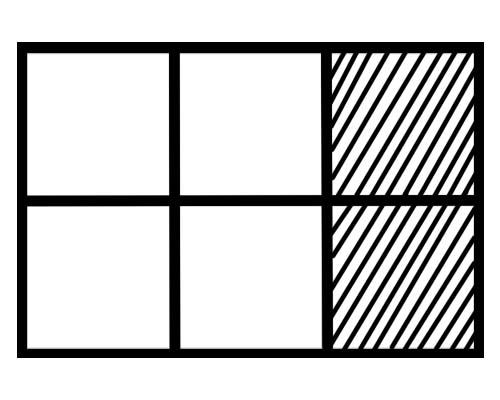
Bu şəkildəki hər hissənin bir hissəsi neçədir? Altı bərabər hissə var, buna görə də hər hissənin bir hissəsi \(\frac{1}{6}\) təşkil edir.
Verilmiş şəkildə bütövün neçə hissəsi kölgədədir? Ümumi 6 hissənin 2 hissəsi kölgəlidir, buna görə də ümumi fraksiya \(\frac{2}{6}\) təşkil edir.
Verilmiş şəkildə bütövün neçə hissəsi kölgə salmayıb? Cəmi 6 hissənin 4 hissəsi kölgələnmir, ona görə də ümumi fraksiya \(\frac{4}{6}\) təşkil edir.
Qrupun bir hissəsini təmsil etmək üçün kəsrdən də istifadə edə bilərik. Nümunə edək ki, 12 şagirdi olan bir sinif müəllimi sinfi 2 bərabər qrupa bölmək istəyir. Hər qrupda 6 tələbə olacaq. 12- \(\frac{1}{2}\) 6-dır 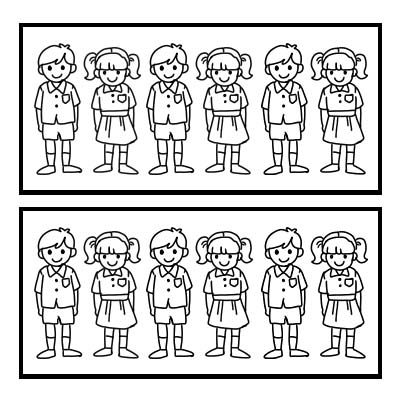
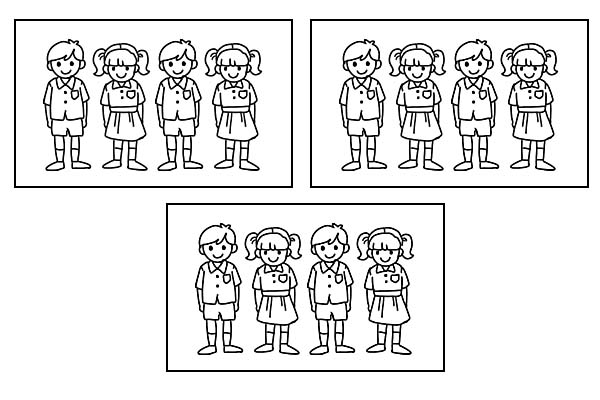
Eyni sinif 3 bərabər qrupa bölünərsə, hər qrupda 4 şagird olur. 12-dən \(\frac{1}{3}\) 4 olduğu üçün.
Aşağıda müzakirə edildiyi kimi müxtəlif fraksiya növləri var:
Düzgün fraksiyalar
Düzgün kəsr bütövün bir hissəsini təmsil edən ədəddir. Düzgün kəsrdə məxrəcdəki rəqəm tamın bölündüyü hissələrin sayını, paylayıcıdakı rəqəm isə alınan hissələrin sayını göstərir. Düzgün kəsr birdən kiçik, payı məxrəcdən kiçik olan kəsrdir.
Misal üçün,
\(\frac{2}{5}\) yəni cəmi 5 hissədən 2 hissə
\(\frac{3}{7}\) yəni cəmi 7 hissədən 3 hissə
Səhv fraksiyalar
Numeratorun məxrəcdən böyük olduğu kəsrə qeyri-düzgün kəsr deyilir.
Misal üçün,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) …. və s.
Qarışıq fraksiyalar
Tam və hissənin birləşməsinə qarışıq kəsr deyilir.
Misal üçün,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...və s.
Düzgün olmayan kəsrin qarışıq kəsrə çevrilməsi
Düzgün olmayan kəsr hissəni və qalığını almaq üçün payı düzgün kəsrin məxrəcinə bölmək yolu ilə qarışıq kəsr kimi ifadə edilə bilər. Sonra qarışıq fraksiya olacaq
Qarışıq kəsr = Hissə (Qalıq ∕ Bölən)
Qarışıq kəsrin düzgün olmayan kəsrə çevrilməsi
Qarışıq kəsr aşağıdakı şəkildə yazmaqla düzgün olmayan kəsr şəklində yazıla bilər:
[(Bütün × Məxrəc) + Numerator)] ∕ Məxrəc
Fraksiyalar kimi
Məxrəci eyni olan kəsrlərə kəsr kimi deyilir.
Misal üçün,
\(\frac{3}{10}\) , \(\frac{4}{10}\) və \(\frac{7}{10}\) kəsr kimidir
Fraksiyalardan fərqli olaraq
Fərqli məxrəcləri olan kəsrlərin kəsrlərdən fərqli olduğu deyilir.
Misal üçün,
\(\frac{3}{7}\) , \(\frac{5}{9}\) və \(\frac{2}{15}\) fraksiyalardan fərqlidir
Ekvivalent kəsrlər
Tamın eyni hissəsini təmsil edən kəsrlərə ekvivalent kəsr deyilir.
Misal üçün,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Kəsirin ən sadə forması
Kəsirin payı və məxrəcində birdən başqa ortaq amil yoxdursa, kəsrə ən sadə və ya ən aşağı formada deyilir. Kəsirin ən sadə formasını onun payını və məxrəcini ən yüksək ümumi əmsala (HCF) bölmək yolu ilə də tapmaq olar. Tutaq ki, yuxarıdakı misalda birinci kəsr \(\frac{1}{2}\) ən sadə formadadır, çünki 1 və 2-nin birindən başqa ümumi amili yoxdur; ikinci fraksiya \(\frac{2}{4}\) ən sadə formada deyil, çünki 2 və 4-ün iki ümumi amili var – 1 və 2, əgər 2 və 4-ü ən yüksək ümumi əmsala, yəni 2-yə bölsək, \(\frac{2}{4}\) indi kəsrin ən sadə forması olan \(\frac{1}{2}\) olacaq.