একটি ভগ্নাংশ একটি সমগ্র একটি অংশ. একটি সম্পূর্ণ বা পূর্ণ বস্তু একটি সমগ্র. একটি সম্পূর্ণ বস্তুর একটি গ্রুপ বা একটি একক বস্তু হতে পারে। যখন আমরা একটি সম্পূর্ণ জিনিসকে সমান ভাগে ভাগ করি, তখন প্রতিটি অংশকে ভগ্নাংশ বলা হয়।
নীচের ছবিতে, একটি পূর্ণ আপেল দুটি ভাগে বিভক্ত। প্রতিটি অর্ধেক হল একটি ভগ্নাংশ যা \(\frac{1}{2}\) হিসাবে উপস্থাপিত হয় যেখানে 1 হল লব এবং 2 হল হর।

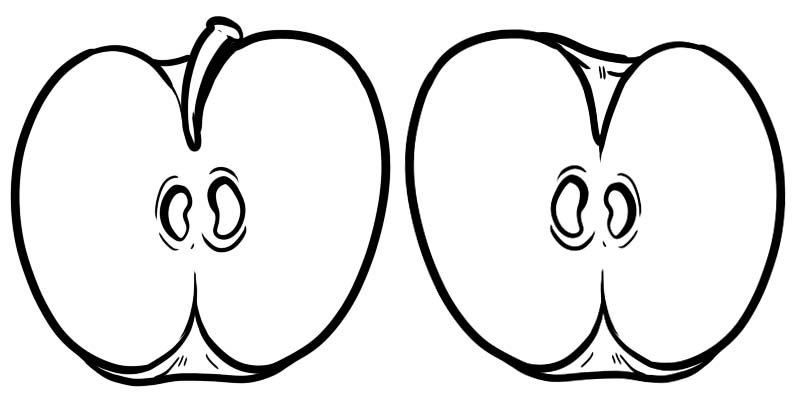
একটি ভগ্নাংশ দুটি সংখ্যা দ্বারা গঠিত যা একটি রেখা দ্বারা বিভক্ত।
লাইনের নিচে যে সংখ্যাটি লেখা থাকে তাকে হর বলা হয়। ডিনোমিনেটর দেখায় কোন কিছুকে কতগুলি সমান ভাগে ভাগ করা হয়েছে।
লাইনের উপরে যে সংখ্যাটি লেখা থাকে তাকে লব বলে। লব দেখায় যে সমগ্রের কয়টি অংশ নেওয়া হয়েছে।
লব হর থেকে বড় বা ছোট হতে পারে।
হর শূন্য বা একের সমান নয়।
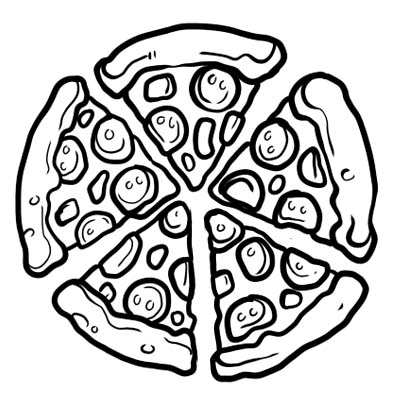
একটি পিজা পাঁচটি সমান অংশে বিভক্ত। আপনি যদি পিজ্জার একটি মাত্র স্লাইস খান তাহলে এর মানে হল আপনি পুরো \(\frac{1}{5}\) খেয়েছেন। \(\frac{1}{5}\) এখানে ভগ্নাংশ।
অর্ধেক এবং কোয়ার্টার
হ্যারি এবং জ্যাক ক্ষুধার্ত ছিল। তারা একটি কাপ কেক কিনল। তারা কাপকেকটিকে দুটি সমান ভাগে ভাগ করে ভাগ করেছে:

এখানে, পার্ট 1 এবং পার্ট 2 হল কাপকেকের দুটি ভগ্নাংশ। পার্ট 1 এক অর্ধেক এবং পার্ট 2 অন্য অর্ধেক।
কোয়ার্টার (1/4) এবং তিন-চতুর্থাংশ (3/4)
হ্যারি, জ্যাক, স্যাম এবং অলিভার চকোলেটের একটি বার কিনলেন। তারা এটি 4 সমান অংশে কাটা।
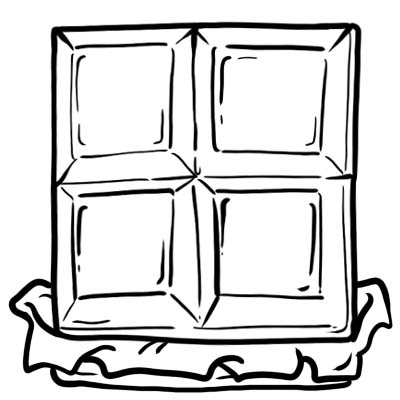
চকলেটের প্রতিটি অংশ বা কিউব এক-চতুর্থাংশ অর্থাৎ \(\frac{1}{4}\)
এর অর্থ হল, একটি সম্পূর্ণ চকলেট চারটি সমান ভাগে বিভক্ত।
ধরুন, জ্যাক তার চকলেটের অংশ খেয়েছে, আমরা বলতে পারি সে চকোলেটের এক-চতুর্থাংশ বা \(\frac{1}{4}\) খেয়েছে। এখন কত চকলেট বাকি আছে? 3টি অংশ বাকি আছে, তাই আমরা বলতে পারি যে \(\frac{3}{4}\) বা তিন-চতুর্থাংশ চকলেট বাকি আছে।
নিচের চিত্রটি দেখে নিন,
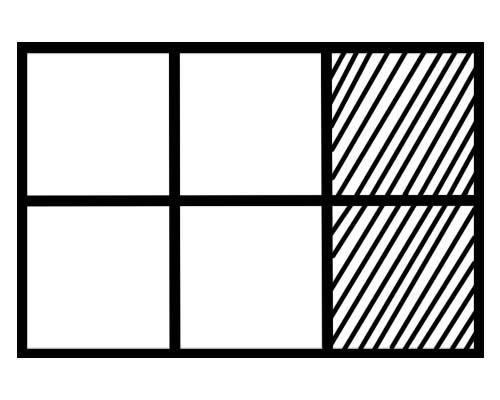
এই চিত্রের প্রতিটি অংশের ভগ্নাংশ কত? ছয়টি সমান অংশ আছে, তাই প্রতিটি অংশের একটি ভগ্নাংশ হল \(\frac{1}{6}\) ।
প্রদত্ত চিত্রে সমগ্রের কয়টি অংশ ছায়াযুক্ত? মোট 6টি অংশের 2টি অংশ ছায়াযুক্ত, তাই মোট ভগ্নাংশ হল \(\frac{2}{6}\) ।
প্রদত্ত চিত্রে সমগ্রের কয়টি অংশ ছায়াযুক্ত নয়? মোট 6টি অংশের 4টি অংশ ছায়াযুক্ত নয়, তাই মোট ভগ্নাংশ হল \(\frac{4}{6}\) ।
আমরা একটি গ্রুপের একটি অংশকে প্রতিনিধিত্ব করতে একটি ভগ্নাংশ ব্যবহার করতে পারি। 12 জন ছাত্র আছে এমন একটি ক্লাসের উদাহরণ নেওয়া যাক এবং ক্লাস শিক্ষক ক্লাসটিকে 2টি সমান গ্রুপে ভাগ করতে চান। প্রতিটি গ্রুপে ৬ জন করে শিক্ষার্থী থাকবে। \(\frac{1}{2}\) 12 এর 6 হল 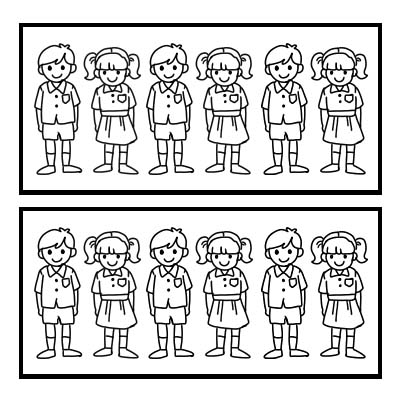
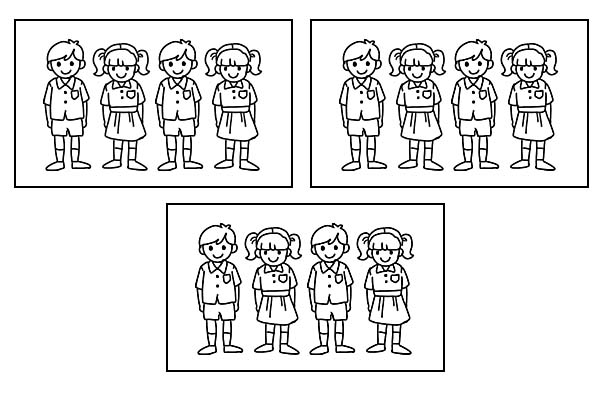
একই শ্রেণীকে 3টি সমান দলে ভাগ করা হলে, প্রতিটি গ্রুপে 4 জন শিক্ষার্থী থাকবে। যেহেতু 12-এর \(\frac{1}{3}\) হল 4।
নিচে আলোচনা করা হয়েছে বিভিন্ন ধরনের ভগ্নাংশ আছে:
সঠিক ভগ্নাংশ
একটি সঠিক ভগ্নাংশ হল একটি সংখ্যা যা একটি সম্পূর্ণ অংশের প্রতিনিধিত্ব করে। একটি সঠিক ভগ্নাংশে, হর-এর সংখ্যাটি দেখায় যে সমস্ত অংশে সম্পূর্ণ ভাগ করা হয়েছে, যখন লবের সংখ্যাটি নেওয়া হয়েছে এমন অংশগুলির সংখ্যা দেখায়। একটি সঠিক ভগ্নাংশ হল একটি ভগ্নাংশ যা একের চেয়ে কম, লবটি হর থেকে কম।
উদাহরণ স্বরূপ,
\(\frac{2}{5}\) অর্থাৎ মোট 5টি অংশের মধ্যে 2টি অংশ
\(\frac{3}{7}\) অর্থাৎ মোট ৭টি অংশের মধ্যে ৩টি অংশ
অনুপযুক্ত ভগ্নাংশ
যে ভগ্নাংশে লব হর থেকে বড় তাকে অনুপযুক্ত ভগ্নাংশ বলে।
উদাহরণ স্বরূপ,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….ইত্যাদি।
মিশ্র ভগ্নাংশ
সম্পূর্ণ এবং একটি অংশের সমন্বয়কে মিশ্র ভগ্নাংশ বলে।
উদাহরণ স্বরূপ,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...ইত্যাদি।
একটি অনুপযুক্ত ভগ্নাংশকে মিশ্র ভগ্নাংশে রূপান্তর করা
ভাগফল এবং অবশিষ্টাংশ পাওয়ার জন্য অনুপযুক্ত ভগ্নাংশের হর দ্বারা লবকে ভাগ করে একটি অনুপযুক্ত ভগ্নাংশকে মিশ্র ভগ্নাংশ হিসাবে প্রকাশ করা যেতে পারে। তাহলে মিশ্র ভগ্নাংশ হবে
মিশ্র ভগ্নাংশ = ভাগফল (অবশিষ্ট ∕ ভাজক)
একটি মিশ্র ভগ্নাংশকে একটি অনুপযুক্ত ভগ্নাংশে রূপান্তর করা
একটি মিশ্র ভগ্নাংশকে নিম্নোক্তভাবে লিখে ভুল ভগ্নাংশের আকারে লেখা যেতে পারে:
[(সম্পূর্ণ × হর) + লব)] ∕ হর
ভগ্নাংশ মত
একই হর সহ ভগ্নাংশগুলিকে ভগ্নাংশের মতো বলা হয়।
উদাহরণ স্বরূপ,
\(\frac{3}{10}\) , \(\frac{4}{10}\) এবং \(\frac{7}{10}\) ভগ্নাংশের মতো
ভগ্নাংশ থেকে ভিন্ন
বিভিন্ন হর সহ ভগ্নাংশকে ভগ্নাংশের বিপরীত বলা হয়।
উদাহরণ স্বরূপ,
\(\frac{3}{7}\) , \(\frac{5}{9}\) এবং \(\frac{2}{15}\) ভগ্নাংশের বিপরীত
সমতুল্য ভগ্নাংশ
যে ভগ্নাংশগুলি সমগ্রের একই অংশের প্রতিনিধিত্ব করে তাকে সমতুল্য ভগ্নাংশ বলা হয়।
উদাহরণ স্বরূপ,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
ভগ্নাংশের সহজতম রূপ
একটি ভগ্নাংশকে তার সহজতম আকারে বা তার সর্বনিম্ন আকারে বলা হয় যদি এর লব এবং হর এর একটি ছাড়া কোন সাধারণ গুণনীয়ক না থাকে। একটি ভগ্নাংশের সহজতম রূপটি তার লব এবং হরকে এর সর্বোচ্চ সাধারণ গুণনীয়ক (HCF) দ্বারা ভাগ করেও পাওয়া যেতে পারে। বলুন, উপরের উদাহরণে, প্রথম ভগ্নাংশ \(\frac{1}{2}\) এর সহজতম আকারে রয়েছে কারণ 1 এবং 2-এর একটি ছাড়া কোনো সাধারণ গুণনীয়ক নেই; দ্বিতীয় ভগ্নাংশ \(\frac{2}{4}\) এর সহজতম আকারে নয় কারণ 2 এবং 4 এর দুটি সাধারণ গুণনীয়ক রয়েছে - 1 এবং 2, যদি আমরা 2 এবং 4 কে সর্বোচ্চ সাধারণ গুণনীয়ক অর্থাৎ 2 দ্বারা ভাগ করি তাহলে \(\frac{2}{4}\) হয়ে যাবে \(\frac{1}{2}\) যা এখন ভগ্নাংশের সহজতম রূপ।