Ein Bruchteil ist ein Teil eines Ganzen. Ein vollständiges oder vollständiges Objekt ist ein Ganzes. Ein Ganzes kann eine Gruppe von Objekten oder ein einzelnes Objekt sein. Wenn wir eine ganze Sache in gleiche Teile teilen, dann nennt man jeden Teil einen Bruch.
In der Abbildung unten ist ein voller Apfel in zwei Hälften geteilt. Jede Hälfte ist ein Bruch, der als \(\frac{1}{2}\) dargestellt wird, wobei 1 der Zähler und 2 der Nenner ist.

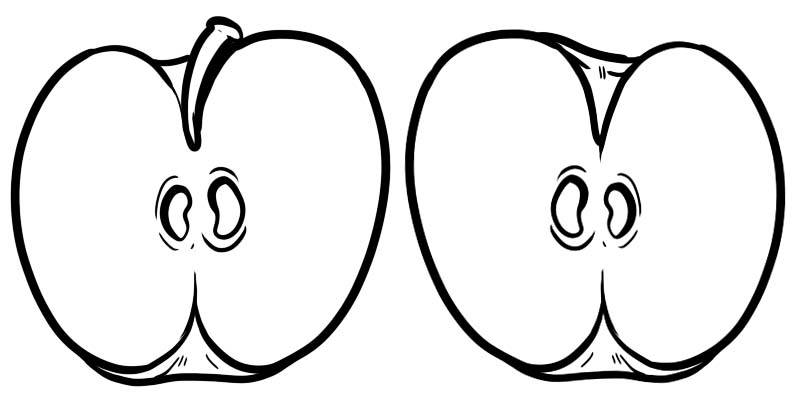
Ein Bruch besteht aus zwei Zahlen, die durch einen Strich geteilt werden.
Die Zahl, die unter dem Strich steht, wird als Nenner bezeichnet. Der Nenner zeigt an, in wie viele gleiche Teile etwas geteilt wurde.
Die Zahl, die über der Linie steht, wird als Zähler bezeichnet. Der Zähler zeigt an, wie viele Teile des Ganzen genommen werden.
Der Zähler kann größer oder kleiner als der Nenner sein.
Der Nenner ist NICHT gleich Null oder Eins.
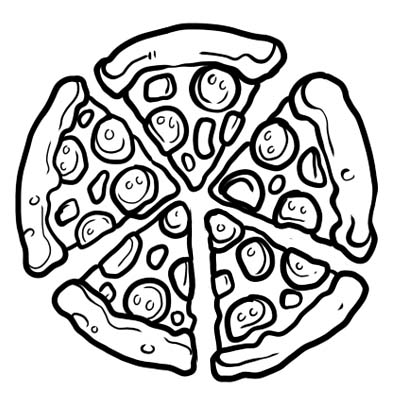
Eine Pizza wird in fünf gleiche Teile geteilt. Wenn du nur ein Stück Pizza isst, bedeutet das, dass du \(\frac{1}{5}\) von der ganzen Pizza gegessen hast. \(\frac{1}{5}\) ist hier der Bruch.
Hälften und Viertel
Harry und Jack waren hungrig. Sie kauften einen Cupcake. Sie teilten den Cupcake, indem sie ihn in zwei gleiche Teile teilten:

Hier sind Teil 1 und Teil 2 zwei Fraktionen des Cupcakes. Teil 1 ist eine Hälfte und Teil 2 ist eine andere Hälfte.
Viertel (1/4) und Dreiviertel (3/4)
Harry, Jack, Sam und Oliver kauften eine Tafel Schokolade. Sie schneiden es in 4 gleiche Teile.
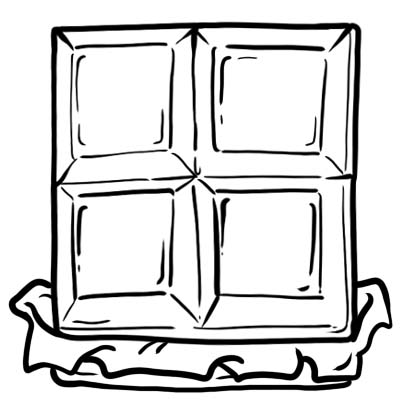
Jeder Teil oder Würfel Schokolade ist ein Viertel, dh \(\frac{1}{4}\)
Das bedeutet, dass eine ganze Schokolade in vier gleiche Teile geteilt wird.
Angenommen, Jack hat seinen Teil der Schokolade gegessen, dann können wir sagen, dass er ein Viertel oder \(\frac{1}{4}\) der Schokolade gegessen hat. Wie viel Schokolade ist jetzt noch übrig? 3 Teile sind übrig, also können wir sagen, dass \(\frac{3}{4}\) oder drei Viertel Schokolade übrig ist.
Schauen Sie sich die folgende Abbildung an,
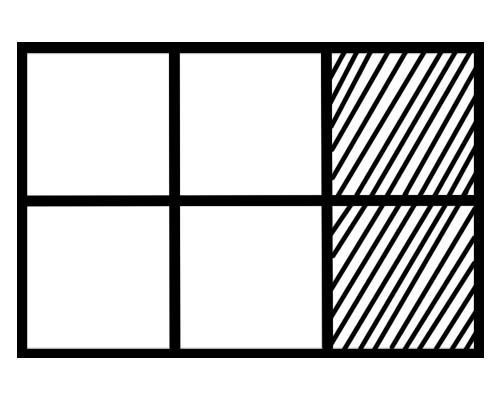
Was ist ein Bruchteil jedes Teils in dieser Figur? Es gibt sechs gleiche Teile, also ist ein Bruchteil jedes Teils \(\frac{1}{6}\) .
Wie viele Teile des Ganzen sind in der gegebenen Abbildung schattiert? 2 Teile der insgesamt 6 Teile sind schattiert, also ist der Gesamtbruch \(\frac{2}{6}\) .
Wie viele Teile des Ganzen sind in der gegebenen Abbildung nicht schattiert? 4 Teile der insgesamt 6 Teile sind nicht schattiert, also ist der Gesamtbruch \(\frac{4}{6}\) .
Wir können auch einen Bruch verwenden, um einen Teil einer Gruppe darzustellen. Nehmen wir als Beispiel eine Klasse mit 12 Schülern und der Klassenlehrer möchte die Klasse in 2 gleich große Gruppen aufteilen. Jede Gruppe besteht aus 6 Schülern. \(\frac{1}{2}\) von 12 ist 6 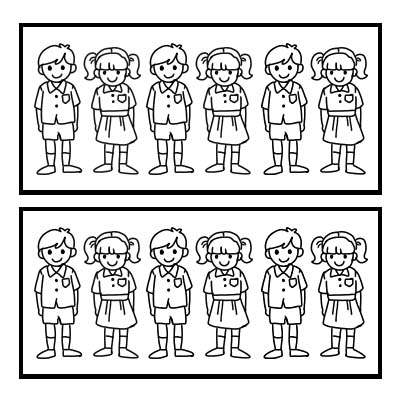
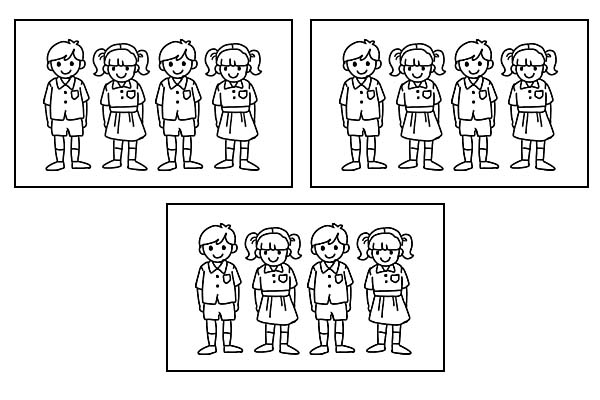
Wenn dieselbe Klasse in 3 gleich große Gruppen geteilt wird, hat jede Gruppe 4 Schüler. Da \(\frac{1}{3}\) von 12 gleich 4 ist.
Es gibt verschiedene Arten von Brüchen, wie unten beschrieben:
Echte Brüche
Ein echter Bruch ist eine Zahl, die einen Teil eines Ganzen darstellt. Bei einem echten Bruch zeigt die Zahl im Nenner die Anzahl der Teile, in die das Ganze geteilt wird, während die Zahl im Zähler die Anzahl der Teile angibt, die genommen wurden. Ein echter Bruch ist ein Bruch, der kleiner als eins ist, wobei der Zähler kleiner als der Nenner ist.
Zum Beispiel,
\(\frac{2}{5}\) also 2 Teile von insgesamt 5 Teilen
\(\frac{3}{7}\) also 3 Teile von insgesamt 7 Teilen
Unechte Brüche
Ein Bruch, bei dem der Zähler größer als der Nenner ist, wird als unechter Bruch bezeichnet.
Zum Beispiel,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….etc.
Gemischte Fraktionen
Eine Kombination aus einem Ganzen und einem Teil wird als gemischter Bruch bezeichnet.
Zum Beispiel,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...etc.
Umwandlung eines unechten Bruchs in einen gemischten Bruch
Ein unechter Bruch kann als gemischter Bruch ausgedrückt werden, indem der Zähler durch den Nenner des unechten Bruchs dividiert wird, um den Quotienten und den Rest zu erhalten. Dann wird der gemischte Bruch sein
Gemischter Bruch = Quotient (Rest ∕ Divisor)
Umwandlung eines gemischten Bruchs in einen unechten Bruch
Ein gemischter Bruch kann in Form eines unechten Bruchs geschrieben werden, indem man ihn folgendermaßen schreibt:
[(Ganzes × Nenner) + Zähler)] ∕ Nenner
Wie Brüche
Brüche mit gleichem Nenner heißen wie Brüche.
Zum Beispiel,
\(\frac{3}{10}\) , \(\frac{4}{10}\) und \(\frac{7}{10}\) sind wie Brüche
Im Gegensatz zu Brüchen
Brüche mit unterschiedlichen Nennern werden als ungleiche Brüche bezeichnet.
Zum Beispiel,
\(\frac{3}{7}\) , \(\frac{5}{9}\) und \(\frac{2}{15}\) sind ungleiche Brüche
Äquivalente Brüche
Brüche, die den gleichen Teil eines Ganzen darstellen, heißen äquivalente Brüche.
Zum Beispiel,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Die einfachste Form eines Bruchs
Ein Bruch heißt in seiner einfachsten Form oder in seiner niedrigsten Form, wenn Zähler und Nenner keinen gemeinsamen Teiler außer Eins haben. Die einfachste Form eines Bruchs kann man auch finden, indem man seinen Zähler und Nenner durch seinen höchsten gemeinsamen Teiler (HCF) dividiert. Angenommen, im obigen Beispiel ist der erste Bruch \(\frac{1}{2}\) in seiner einfachsten Form, da 1 und 2 keinen gemeinsamen Faktor außer einem haben; der zweite Bruch \(\frac{2}{4}\) ist nicht in seiner einfachsten Form, weil 2 und 4 zwei gemeinsame Teiler haben – 1 und 2, wenn wir 2 und 4 durch den höchsten gemeinsamen Teiler dividieren, also 2, dann \(\frac{2}{4}\) wird zu \(\frac{1}{2}\) was nun die einfachste Form des Bruchs ist.