A fraction is a part of a whole. A complete or full object is a whole. A whole can be a group of objects or a single object. When we divide a whole thing into equal parts, then each part is called a fraction.
In the below image, one full apple is divided into two halves. Each half is a fraction represented as \(\frac{1}{2}\) where 1 is the numerator and 2 is the denominator.

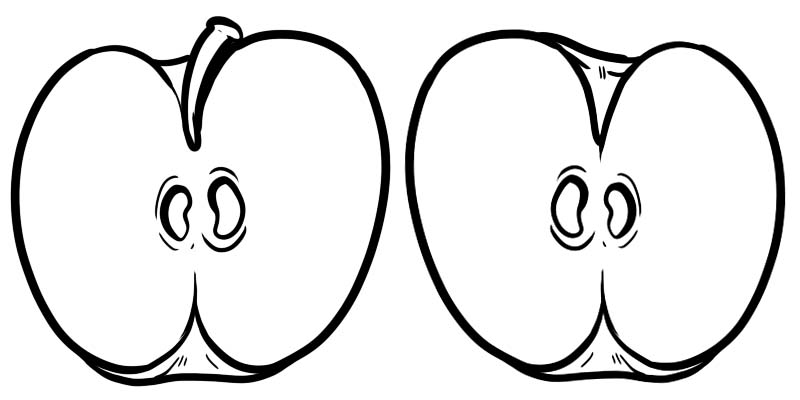
A fraction is made up of two numbers which are divided by a line.
The number that is written below the line is known as the denominator. Denominator shows how many equal parts something has been divided into.
The number that is written above the line is known as the numerator. The numerator shows how many parts of the whole are taken.
The numerator can be greater or smaller than the denominator.
The denominator is NOT equal to zero or one.
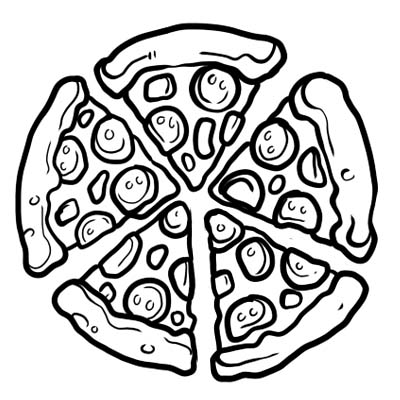
A pizza is divided into five equal parts. If you eat only one slice of the pizza, it means you ate \(\frac{1}{5}\) of the whole pizza. \(\frac{1}{5}\)is the fraction here.
Halves and Quarters
Harry and Jack were hungry. They bought a cupcake. They shared the cupcake by dividing it into two equal parts:

Here, Part 1 and Part 2 are two fractions of the cupcake. Part 1 is one half and Part 2 is another half.
Quarters (1/4) and Three-Quarters (3/4)
Harry, Jack, Sam, and Oliver bought a bar of chocolate. They cut it into 4 equal parts.
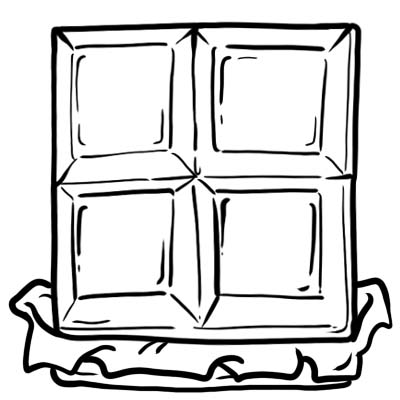
Each part or cube of chocolate is one-quarter i.e. \(\frac{1}{4}\)
This means, one whole chocolate divided into four equal parts.
Suppose, Jack ate his part of chocolate, we can say he ate one-fourth or \(\frac{1}{4}\) of the chocolate. How much chocolate is now left? 3 parts are left, so we can say that \(\frac{3}{4}\) or three-quarters of chocolate is left.
Take a look at the figure given below,
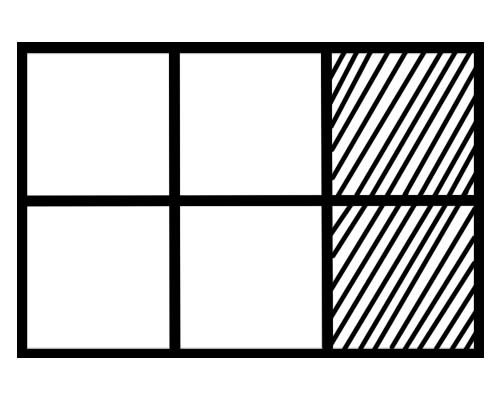
What is a fraction of each part in this figure? There are six equal parts, so a fraction of each part is \(\frac{1}{6}\).
How many parts of the whole are shaded in the given figure? 2 parts of the total 6 parts are shaded, so the total fraction is \(\frac{2}{6}\).
How many parts of the whole are not shaded in the given figure? 4 parts of the total 6 parts are not shaded, so the total fraction is \(\frac{4}{6}\).
We can also use a fraction to represent a part of a group. Let's take an example of a class having 12 students and the class teacher wants to divide the class into 2 equal groups. Each group will have 6 students. \(\frac{1}{2}\)of 12 is 6
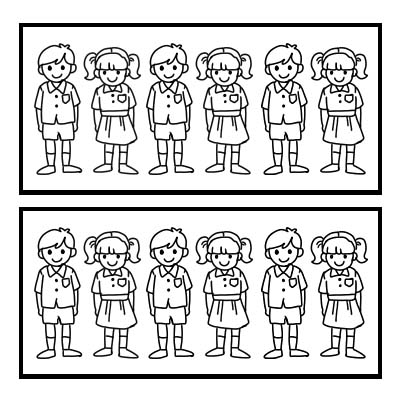
If the same class is divided into 3 equal groups, each group will have 4 students. As \(\frac{1}{3}\) of 12 is 4.
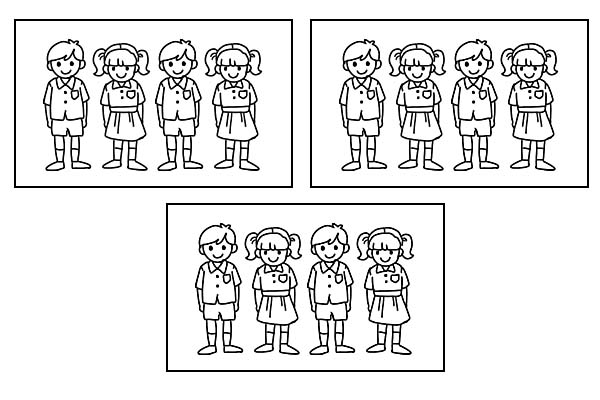
There are different types of fractions as discussed below:
Proper fractions
A proper fraction is a number representing a part of a whole. In a proper fraction, the number in the denominator shows the number of parts into which the whole is divided, while the number in the numerator shows the number of parts that have been taken. A proper fraction is a fraction that is less than one, with the numerator less than the denominator.
For example,
\(\frac{2}{5}\) i.e. 2 parts out of the total of 5 parts
\(\frac{3}{7}\)i.e. 3 parts out of the total of 7 parts
Improper fractions
A fraction in which the numerator is bigger than the denominator is called an improper fraction.
For example,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\)….etc.
Mixed fractions
A combination of a whole and a part is called a mixed fraction.
For example,
3\(\frac{1}{2}\)
4\(\frac{3}{4}\)...etc.
Conversion of an improper fraction into a mixed fraction
An improper fraction can be expressed as a mixed fraction by dividing the numerator by the denominator of the improper fraction to obtain the quotient and the remainder. Then the mixed fraction will be
Mixed Fraction = Quotient (Remainder ∕ Divisor)
Conversion of a mixed fraction into an improper fraction
A mixed fraction can be written in the form of an improper fraction by writing it in the following way:
[(Whole × Denominator) + Numerator)] ∕ Denominator
Like fractions
Fractions with the same denominator are said to be like fractions.
For example,
\(\frac{3}{10}\), \(\frac{4}{10}\) and \(\frac{7}{10}\) are like fractions
Unlike fractions
Fractions with different denominators are said to be unlike fractions.
For example,
\(\frac{3}{7}\), \(\frac{5}{9}\)and \(\frac{2}{15}\)are unlike fractions
Equivalent fractions
Fractions that represent the same part of a whole are said to be equivalent fractions.
For example,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\)= \(\frac{4}{8}\) = \(\frac{5}{10}\)= \(\frac{6}{12}\)…..
The simplest form of a fraction
A fraction is said to be in its simplest form or its lowest form if its numerator and denominator have no common factor except one. The simplest form of a fraction can also be found by dividing its numerator and denominator by its highest common factor (HCF). Say, in the above example, the first fraction \(\frac{1}{2}\) is in its simplest form as 1 and 2 have no common factor except one; the second fraction\(\frac{2}{4}\) is not in its simplest form because 2 and 4 have two common factors – 1 and 2, if we divide 2 and 4 by the highest common factor i.e. 2 then \(\frac{2}{4}\)will become\(\frac{1}{2}\) which is now the simplest form of the fraction.