Una fracción es una parte de un todo. Un objeto completo o completo es un todo. Un todo puede ser un grupo de objetos o un solo objeto. Cuando dividimos un todo en partes iguales, entonces cada parte se llama fracción.
En la imagen de abajo, una manzana completa se divide en dos mitades. Cada mitad es una fracción representada como \(\frac{1}{2}\) donde 1 es el numerador y 2 es el denominador.

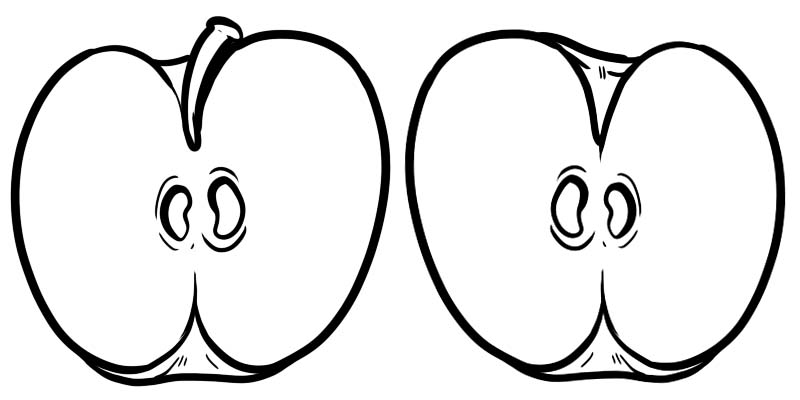
Una fracción se compone de dos números que se dividen por una línea.
El número que se escribe debajo de la línea se conoce como denominador. El denominador muestra en cuántas partes iguales se ha dividido algo.
El número que se escribe encima de la línea se conoce como numerador. El numerador muestra cuántas partes del todo se toman.
El numerador puede ser mayor o menor que el denominador.
El denominador NO es igual a cero o uno.
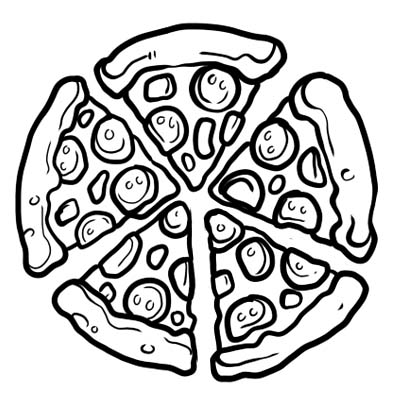
Una pizza se divide en cinco partes iguales. Si comes solo una rebanada de pizza, significa que te comiste \(\frac{1}{5}\) de toda la pizza. \(\frac{1}{5}\) es la fracción aquí.
mitades y cuartos
Harry y Jack tenían hambre. Compraron una magdalena. Compartieron el cupcake dividiéndolo en dos partes iguales:

Aquí, la Parte 1 y la Parte 2 son dos fracciones de la magdalena. La parte 1 es la mitad y la parte 2 es otra mitad.
Cuartos (1/4) y Tres Cuartos (3/4)
Harry, Jack, Sam y Oliver compraron una barra de chocolate. Lo cortaron en 4 partes iguales.
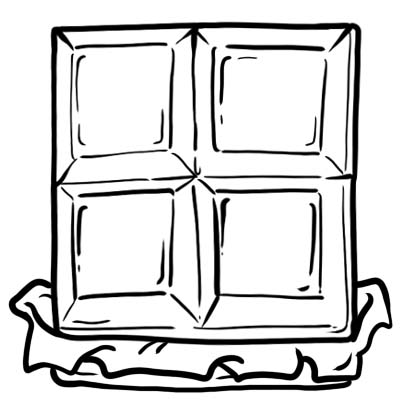
Cada parte o cubo de chocolate es un cuarto, es decir \(\frac{1}{4}\)
Es decir, un chocolate entero dividido en cuatro partes iguales.
Supongamos que Jack comió su parte de chocolate, podemos decir que comió un cuarto o \(\frac{1}{4}\) del chocolate. ¿Cuánto chocolate queda ahora? Quedan 3 partes, entonces podemos decir que quedan \(\frac{3}{4}\) o tres cuartos de chocolate.
Echa un vistazo a la figura que se muestra a continuación,
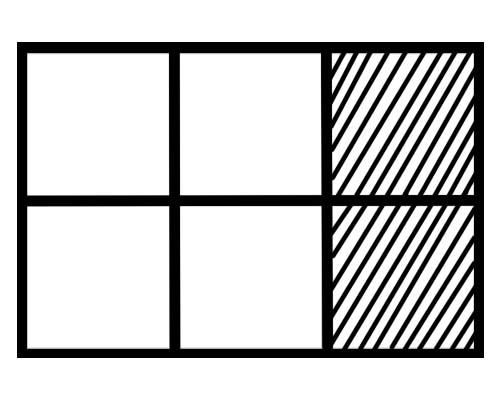
¿Qué es una fracción de cada parte en esta figura? Hay seis partes iguales, por lo que una fracción de cada parte es \(\frac{1}{6}\) .
¿Cuántas partes del todo están sombreadas en la figura dada? 2 partes del total de 6 partes están sombreadas, por lo que la fracción total es \(\frac{2}{6}\) .
¿Cuántas partes del todo no están sombreadas en la figura dada? 4 partes del total de 6 partes no están sombreadas, por lo que la fracción total es \(\frac{4}{6}\) .
También podemos usar una fracción para representar una parte de un grupo. Tomemos un ejemplo de una clase que tiene 12 estudiantes y el profesor de la clase quiere dividir la clase en 2 grupos iguales. Cada grupo tendrá 6 alumnos. \(\frac{1}{2}\) de 12 es 6 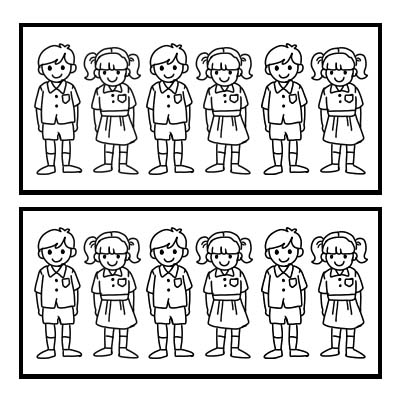
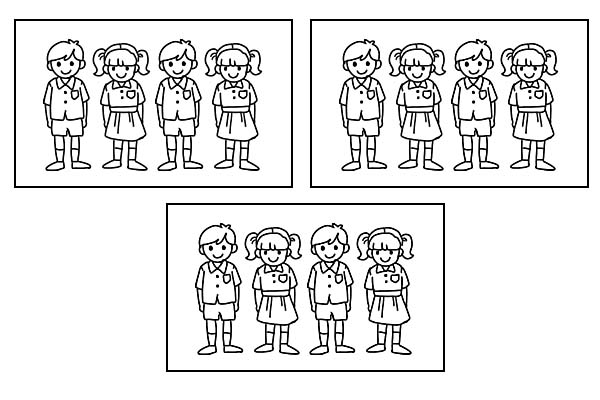
Si la misma clase se divide en 3 grupos iguales, cada grupo tendrá 4 alumnos. Como \(\frac{1}{3}\) de 12 es 4.
Hay diferentes tipos de fracciones como se explica a continuación:
fracciones propias
Una fracción propia es un número que representa una parte de un todo. En una fracción propia, el número en el denominador muestra el número de partes en que se divide el todo, mientras que el número en el numerador muestra el número de partes que se han tomado. Una fracción propia es una fracción que es menor que uno, con el numerador menor que el denominador.
Por ejemplo,
\(\frac{2}{5}\) es decir, 2 partes del total de 5 partes
\(\frac{3}{7}\) es decir, 3 partes del total de 7 partes
fracciones impropias
Una fracción en la que el numerador es mayor que el denominador se llama fracción impropia.
Por ejemplo,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….etc.
fracciones mixtas
La combinación de un todo y una parte se llama fracción mixta.
Por ejemplo,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...etc.
Conversión de una fracción impropia en una fracción mixta
Una fracción impropia se puede expresar como una fracción mixta dividiendo el numerador por el denominador de la fracción impropia para obtener el cociente y el resto. Entonces la fracción mixta será
Fracción Mixta = Cociente (Resto ∕ Divisor)
Conversión de una fracción mixta en una fracción impropia
Una fracción mixta se puede escribir en forma de fracción impropia escribiéndola de la siguiente manera:
[(Entero × Denominador) + Numerador)] ∕ Denominador
como fracciones
Se dice que las fracciones con el mismo denominador son fracciones semejantes.
Por ejemplo,
\(\frac{3}{10}\) , \(\frac{4}{10}\) y \(\frac{7}{10}\) son fracciones semejantes
A diferencia de las fracciones
Las fracciones con diferente denominador se dice que son fracciones diferentes.
Por ejemplo,
\(\frac{3}{7}\) , \(\frac{5}{9}\) y \(\frac{2}{15}\) son fracciones diferentes
Fracciones equivalentes
Las fracciones que representan la misma parte de un todo se llaman fracciones equivalentes.
Por ejemplo,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
La forma más simple de una fracción.
Se dice que una fracción está en su forma más simple o en su forma más baja si su numerador y denominador no tienen factor común excepto uno. La forma más simple de una fracción también se puede encontrar dividiendo su numerador y denominador por su máximo común divisor (HCF). Digamos, en el ejemplo anterior, la primera fracción \(\frac{1}{2}\) está en su forma más simple ya que 1 y 2 no tienen factor común excepto uno; la segunda fracción \(\frac{2}{4}\) no está en su forma más simple porque 2 y 4 tienen dos factores comunes: 1 y 2, si dividimos 2 y 4 por el factor común más alto, es decir, 2, entonces \(\frac{2}{4}\) se convertirá en \(\frac{1}{2}\) que ahora es la forma más simple de la fracción.