کسری جزئی از یک کل است. یک شیء کامل یا کامل یک کل است. یک کل می تواند گروهی از اشیاء یا یک شیء واحد باشد. وقتی یک چیز کامل را به قسمت های مساوی تقسیم می کنیم، آنگاه هر جزء را کسری می گویند.
در تصویر زیر یک سیب پر به دو نیمه تقسیم شده است. هر نیمه کسری است که به صورت \(\frac{1}{2}\) نشان داده می شود که در آن 1 صورت و 2 مخرج است.

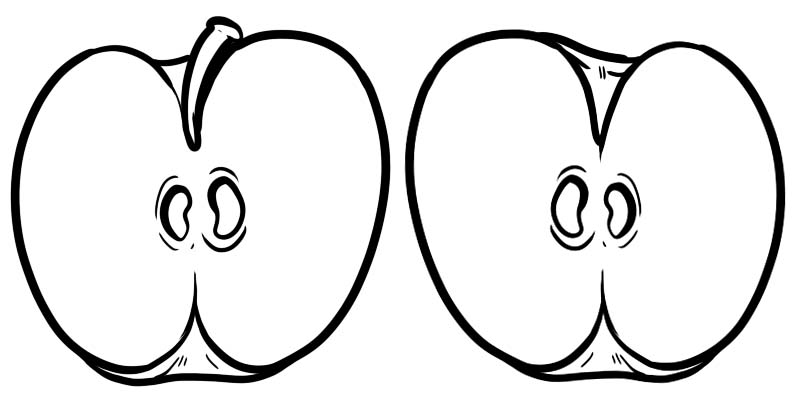
کسری از دو عدد تشکیل شده است که بر یک خط تقسیم می شوند.
عددی که زیر خط نوشته می شود به عنوان مخرج شناخته می شود. مخرج نشان می دهد که چیزی به چند قسمت مساوی تقسیم شده است.
عددی که بالای خط نوشته میشود، به عنوان شمارنده شناخته میشود. شمارنده نشان می دهد که چند جزء از کل گرفته شده است.
صورت می تواند بزرگتر یا کوچکتر از مخرج باشد.
مخرج برابر با صفر یا یک نیست.
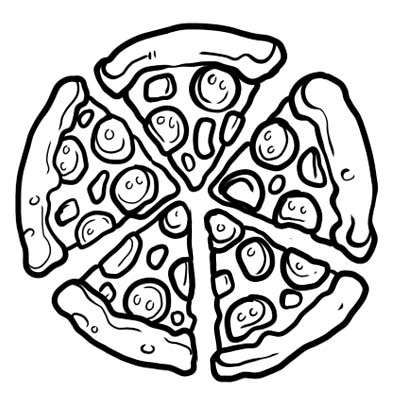
یک پیتزا به پنج قسمت مساوی تقسیم می شود. اگر فقط یک تکه از پیتزا بخورید، به این معنی است \(\frac{1}{5}\) از کل پیتزا را خوردهاید. \(\frac{1}{5}\) در اینجا کسری است.
نیمه ها و ربع ها
هری و جک گرسنه بودند. آنها یک کیک کوچک خریدند. آنها کاپ کیک را با تقسیم آن به دو قسمت مساوی تقسیم کردند:

در اینجا، قسمت 1 و قسمت 2 دو بخش از کیک کوچک هستند. قسمت 1 یک نیمه و قسمت 2 یک نیمه دیگر است.
یک چهارم (1/4) و سه چهارم (3/4)
هری، جک، سم و الیور یک تخته شکلات خریدند. آن را به 4 قسمت مساوی تقسیم می کنند.
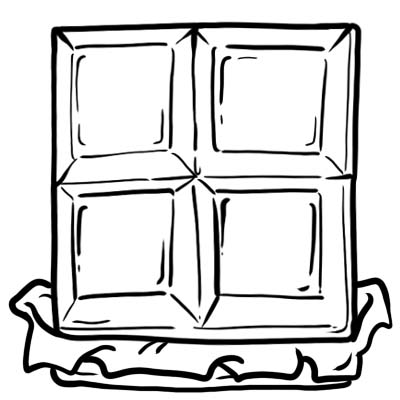
هر قسمت یا مکعب شکلات یک چهارم است یعنی \(\frac{1}{4}\)
یعنی یک شکلات کامل به چهار قسمت مساوی تقسیم می شود.
فرض کنید جک قسمت خود را از شکلات خورد، می توان گفت که او یک چهارم یا \(\frac{1}{4}\) شکلات را خورده است. حالا چقدر شکلات باقی مانده است؟ 3 قسمت باقی مانده است که می توان گفت \(\frac{3}{4}\) یا سه چهارم شکلات باقی مانده است.
به شکل زیر نگاه کنید،
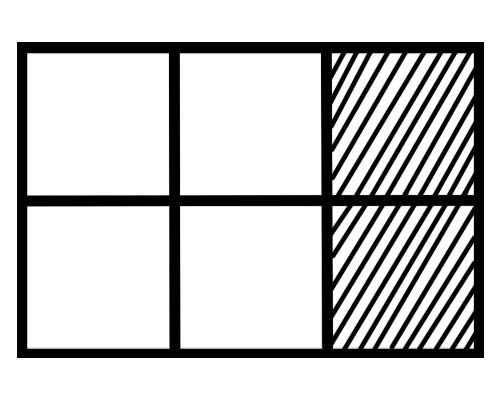
کسری از هر قسمت در این شکل چقدر است؟ شش قسمت مساوی وجود دارد، بنابراین کسری از هر قسمت \(\frac{1}{6}\) است.
چند قسمت از کل در شکل داده شده سایه دار است؟ 2 قسمت از مجموع 6 قسمت سایه دار هستند، بنابراین کسر کل \(\frac{2}{6}\) است.
چند قسمت از کل در شکل داده شده سایه ندارد؟ 4 قسمت از مجموع 6 قسمت سایه ندارند، بنابراین کسر کل \(\frac{4}{6}\) است.
همچنین می توانیم از کسری برای نمایش بخشی از یک گروه استفاده کنیم. بیایید یک کلاس را مثال بزنیم که 12 دانش آموز دارد و معلم کلاس می خواهد کلاس را به 2 گروه مساوی تقسیم کند. هر گروه 6 دانش آموز خواهد داشت. \(\frac{1}{2}\) از 12 برابر 6 است 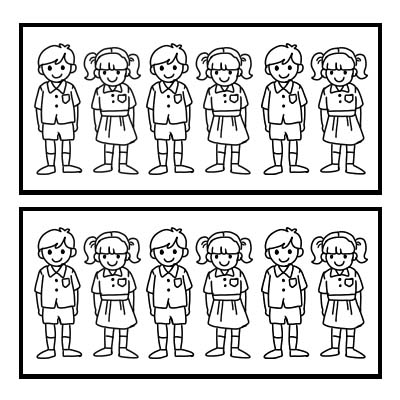
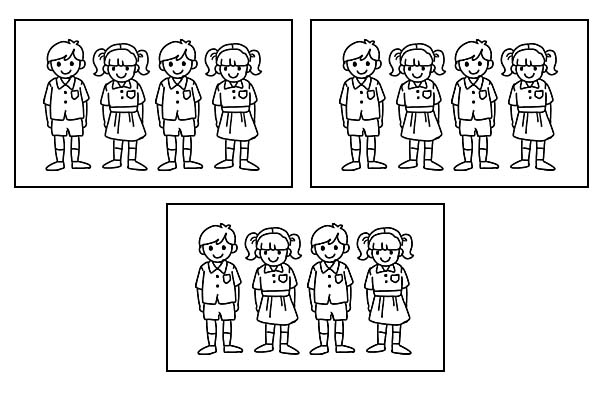
اگر همان کلاس به 3 گروه مساوی تقسیم شود، هر گروه 4 دانش آموز خواهد داشت. به عنوان \(\frac{1}{3}\) از 12 برابر 4 است.
کسرها انواع مختلفی دارند که در زیر به آنها اشاره می شود:
کسرهای مناسب
کسر مناسب عددی است که بخشی از یک کل را نشان می دهد. در کسری مناسب، عدد در مخرج تعداد قسمتهایی را که کل به آن تقسیم میشود، نشان میدهد، در حالی که عدد موجود در صورت، تعداد اجزایی را نشان میدهد که گرفته شدهاند. کسر مناسب کسری است که کوچکتر از یک باشد و صورت آن کوچکتر از مخرج باشد.
مثلا،
\(\frac{2}{5}\) یعنی 2 قسمت از کل 5 قسمت
\(\frac{3}{7}\) یعنی 3 قسمت از مجموع 7 قسمت
کسرهای نامناسب
کسری که صورت آن بزرگتر از مخرج باشد کسر نامناسب نامیده می شود.
مثلا،
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….و غیره.
کسرهای مختلط
به ترکیب یک کل و یک جزء کسر مختلط می گویند.
مثلا،
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ... و غیره.
تبدیل کسر نامناسب به کسر مختلط
کسری نامناسب را می توان به صورت کسر مختلط با تقسیم صورت بر مخرج کسر نامناسب برای بدست آوردن ضریب و باقیمانده بیان کرد. سپس کسر مختلط خواهد بود
کسر مختلط = ضریب (بخش باقیمانده ∕)
تبدیل کسر مختلط به کسر نامناسب
کسر مختلط را می توان به صورت کسر نامناسب با نوشتن آن به صورت زیر نوشت:
[(کل × مخرج) + صورتگر)] ∕ مخرج
مانند کسرها
به کسری با مخرج یکسان گفته می شود که مانند کسر است.
مثلا،
\(\frac{3}{10}\) ، \(\frac{4}{10}\) و \(\frac{7}{10}\) مانند کسری هستند
بر خلاف کسری
به کسری با مخرج های مختلف گفته می شود که شبیه کسرها نیستند.
مثلا،
\(\frac{3}{7}\) ، \(\frac{5}{9}\) و \(\frac{2}{15}\) بر خلاف کسری هستند
کسرهای معادل
به کسرهایی که نمایانگر همان قسمت یک کل هستند، کسرهای هم ارز گفته می شود.
مثلا،
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
ساده ترین شکل کسری
کسری به سادهترین شکل یا پایینترین شکل آن گفته میشود که صورت و مخرج آن هیچ عامل مشترکی جز یک نداشته باشند. ساده ترین شکل یک کسر را نیز می توان با تقسیم صورت و مخرج آن بر بالاترین ضریب مشترک آن (HCF) یافت. مثلاً در مثال بالا، کسر اول \(\frac{1}{2}\) در سادهترین شکل خود است زیرا 1 و 2 هیچ عامل مشترکی به جز یک ندارند. کسر دوم \(\frac{2}{4}\) به ساده ترین شکل خود نیست زیرا 2 و 4 دو عامل مشترک دارند - 1 و 2، اگر 2 و 4 را بر بالاترین عامل مشترک یعنی 2 تقسیم کنیم \(\frac{2}{4}\) به \(\frac{1}{2}\) تبدیل میشود که اکنون سادهترین شکل کسر است.