Une fraction est une partie d'un tout. Un objet complet ou plein est un tout. Un ensemble peut être un groupe d'objets ou un objet unique. Lorsque nous divisons un tout en parties égales, chaque partie s'appelle une fraction.
Dans l'image ci-dessous, une pomme pleine est divisée en deux moitiés. Chaque moitié est une fraction représentée par \(\frac{1}{2}\) où 1 est le numérateur et 2 est le dénominateur.

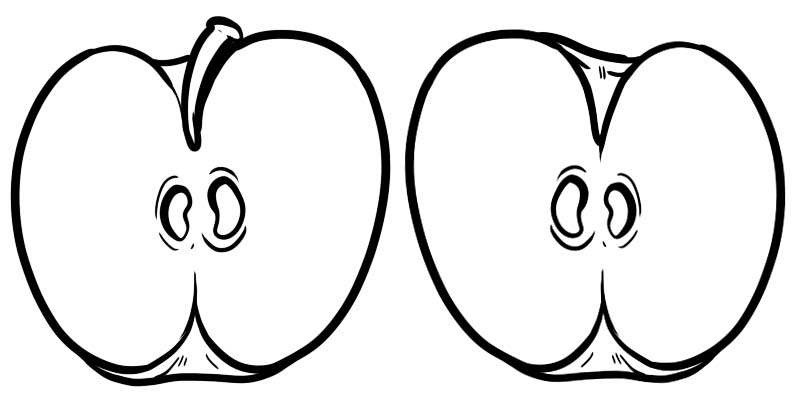
Une fraction est composée de deux nombres divisés par une ligne.
Le nombre écrit sous la ligne est appelé dénominateur. Le dénominateur indique en combien de parties égales quelque chose a été divisé.
Le nombre écrit au-dessus de la ligne est appelé numérateur. Le numérateur indique combien de parties du tout sont prises.
Le numérateur peut être supérieur ou inférieur au dénominateur.
Le dénominateur n'est PAS égal à zéro ou un.
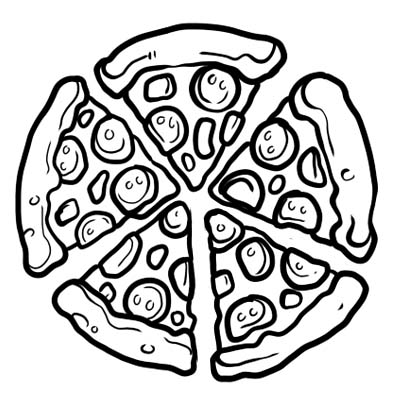
Une pizza est divisée en cinq parties égales. Si vous ne mangez qu'une seule tranche de pizza, cela signifie que vous avez mangé \(\frac{1}{5}\) de toute la pizza. \(\frac{1}{5}\) est la fraction ici.
Moitiés et quarts
Harry et Jack avaient faim. Ils ont acheté un petit gâteau. Ils se sont partagé le cupcake en le divisant en deux parts égales :

Ici, la partie 1 et la partie 2 sont deux fractions du cupcake. La partie 1 est une moitié et la partie 2 est une autre moitié.
Quarts (1/4) et trois quarts (3/4)
Harry, Jack, Sam et Oliver ont acheté une barre de chocolat. Ils le coupent en 4 parties égales.
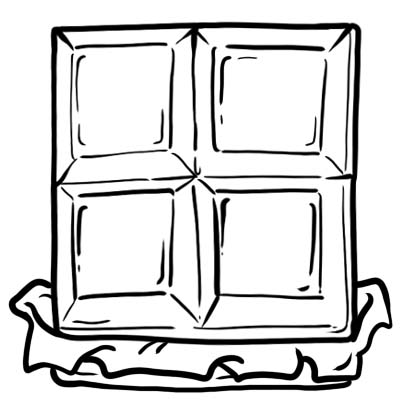
Chaque partie ou cube de chocolat correspond à un quart, c'est-à-dire \(\frac{1}{4}\)
Cela signifie, un chocolat entier divisé en quatre parties égales.
Supposons que Jack ait mangé sa part de chocolat, on peut dire qu'il a mangé un quart ou \(\frac{1}{4}\) du chocolat. Combien de chocolat reste-t-il maintenant ? Il reste 3 parties, on peut donc dire qu'il reste \(\frac{3}{4}\) soit les trois quarts du chocolat.
Jetez un oeil à la figure ci-dessous,
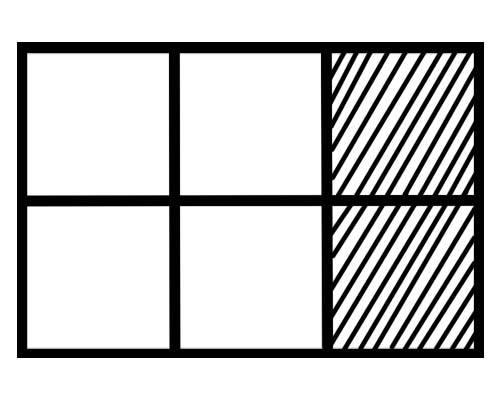
Quelle est une fraction de chaque partie dans cette figure ? Il y a six parties égales, donc une fraction de chaque partie est \(\frac{1}{6}\) .
Combien de parties du tout sont ombrées dans la figure donnée ? 2 parties du total 6 parties sont ombrées, donc la fraction totale est \(\frac{2}{6}\) .
Combien de parties du tout ne sont pas ombrées dans la figure donnée ? 4 parties du total 6 parties ne sont pas ombrées, donc la fraction totale est \(\frac{4}{6}\) .
On peut aussi utiliser une fraction pour représenter une partie d'un groupe. Prenons l'exemple d'une classe de 12 élèves et le maître de classe veut diviser la classe en 2 groupes égaux. Chaque groupe sera composé de 6 élèves. \(\frac{1}{2}\) de 12 est 6 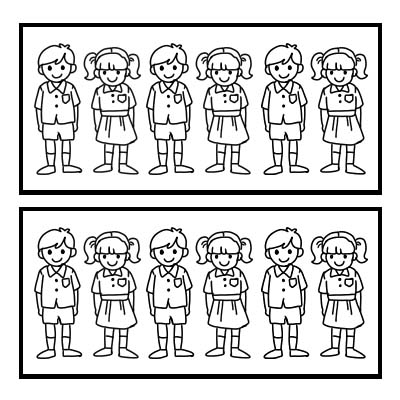
Si une même classe est divisée en 3 groupes égaux, chaque groupe aura 4 élèves. Comme \(\frac{1}{3}\) de 12 est 4.
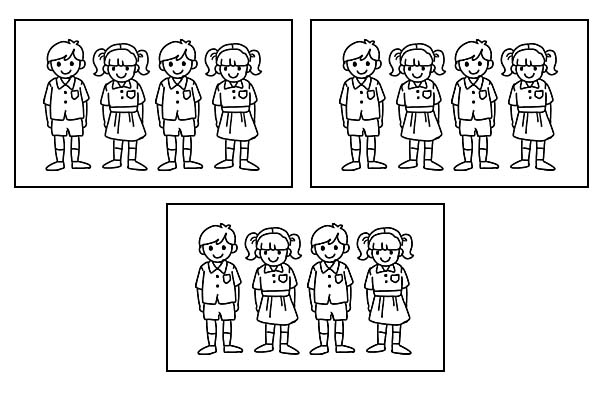
Il existe différents types de fractions, comme indiqué ci-dessous :
Fractions propres
Une fraction propre est un nombre représentant une partie d'un tout. Dans une fraction propre, le nombre au dénominateur indique le nombre de parties dans lesquelles le tout est divisé, tandis que le nombre au numérateur indique le nombre de parties qui ont été prises. Une fraction propre est une fraction inférieure à un, dont le numérateur est inférieur au dénominateur.
Par exemple,
\(\frac{2}{5}\) soit 2 parties sur un total de 5 parties
\(\frac{3}{7}\) soit 3 parties sur un total de 7 parties
Fractions impropres
Une fraction dont le numérateur est plus grand que le dénominateur est appelée fraction impropre.
Par exemple,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) … etc.
Fractions mixtes
Une combinaison d'un tout et d'une partie s'appelle une fraction mixte.
Par exemple,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...etc.
Conversion d'une fraction impropre en fraction mixte
Une fraction impropre peut être exprimée comme une fraction mixte en divisant le numérateur par le dénominateur de la fraction impropre pour obtenir le quotient et le reste. Alors la fraction mixte sera
Fraction Mixte = Quotient (Reste ∕ Diviseur)
Conversion d'une fraction mixte en une fraction impropre
Une fraction mixte peut être écrite sous la forme d'une fraction impropre en l'écrivant de la manière suivante :
[(Entier × Dénominateur) + Numérateur)] ∕ Dénominateur
Comme des fractions
Les fractions ayant le même dénominateur sont dites comme des fractions.
Par exemple,
\(\frac{3}{10}\) , \(\frac{4}{10}\) et \(\frac{7}{10}\) sont comme des fractions
Contrairement aux fractions
Les fractions avec des dénominateurs différents sont dites différentes des fractions.
Par exemple,
\(\frac{3}{7}\) , \(\frac{5}{9}\) et \(\frac{2}{15}\) ne sont pas des fractions
Fractions équivalentes
Les fractions qui représentent la même partie d'un tout sont dites fractions équivalentes.
Par exemple,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
La forme la plus simple d'une fraction
Une fraction est dite sous sa forme la plus simple ou sous sa forme la plus basse si son numérateur et son dénominateur n'ont pas de facteur commun sauf un. La forme la plus simple d'une fraction peut également être trouvée en divisant son numérateur et son dénominateur par son facteur commun le plus élevé (HCF). Supposons que dans l'exemple ci-dessus, la première fraction \(\frac{1}{2}\) est dans sa forme la plus simple car 1 et 2 n'ont pas de facteur commun sauf un ; la deuxième fraction \(\frac{2}{4}\) n'est pas dans sa forme la plus simple car 2 et 4 ont deux facteurs communs - 1 et 2, si nous divisons 2 et 4 par le facteur commun le plus élevé, c'est-à-dire 2, alors \(\frac{2}{4}\) deviendra \(\frac{1}{2}\) qui est maintenant la forme la plus simple de la fraction.