एक अंश पूरे का एक हिस्सा है। एक पूर्ण या पूर्ण वस्तु एक संपूर्ण है। एक संपूर्ण वस्तुओं का समूह या एक वस्तु हो सकता है। जब हम किसी वस्तु को समान भागों में बाँटते हैं तो प्रत्येक भाग भिन्न कहलाता है।
नीचे की छवि में, एक पूर्ण सेब को दो हिस्सों में बांटा गया है। प्रत्येक आधा एक अंश है जिसे \(\frac{1}{2}\) के रूप में दर्शाया गया है जहां 1 अंश है और 2 हर है।

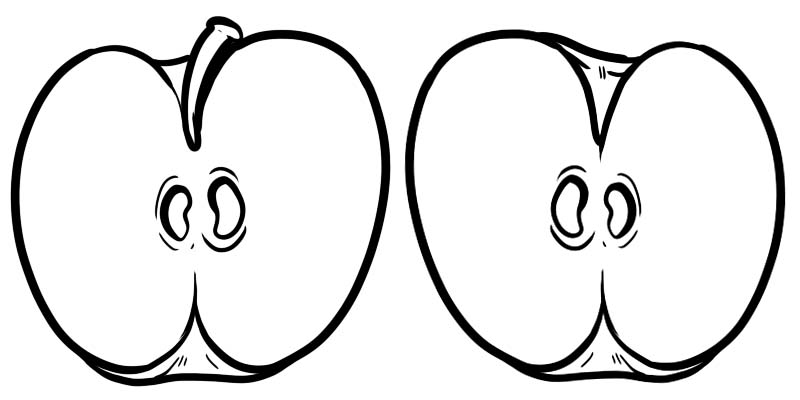
एक भिन्न दो संख्याओं से बनी होती है जो एक रेखा से विभाजित होती हैं।
रेखा के नीचे लिखी गई संख्या को हर कहते हैं। भाजक दर्शाता है कि किसी वस्तु को कितने बराबर भागों में बाँटा गया है।
रेखा के ऊपर जो संख्या लिखी जाती है उसे अंश कहते हैं। अंश दिखाता है कि पूरे के कितने हिस्से लिए गए हैं।
अंश हर से बड़ा या छोटा हो सकता है।
हर शून्य या एक के बराबर नहीं है।
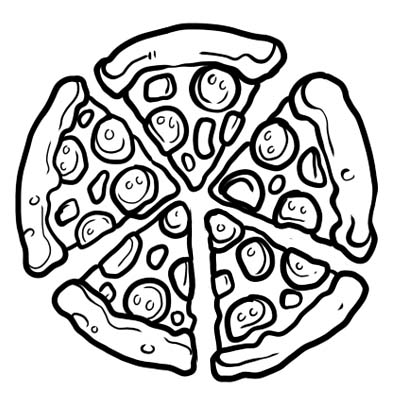
एक पिज्जा को पांच बराबर भागों में बांटा गया है। यदि आप पिज्जा का केवल एक टुकड़ा खाते हैं, तो इसका मतलब है कि आपने पूरे पिज्जा का \(\frac{1}{5}\) खा लिया। \(\frac{1}{5}\) यहां भिन्न है।
आधा और क्वार्टर
हैरी और जैक भूखे थे। उन्होंने एक कपकेक खरीदा। उन्होंने कपकेक को दो बराबर भागों में विभाजित करके साझा किया:

यहाँ, भाग 1 और भाग 2 कपकेक के दो अंश हैं। भाग 1 एक आधा है और भाग 2 दूसरा आधा है।
क्वार्टर (1/4) और तीन-चौथाई (3/4)
हैरी, जैक, सैम और ओलिवर ने चॉकलेट का एक बार खरीदा। उन्होंने इसे 4 बराबर भागों में काट दिया।
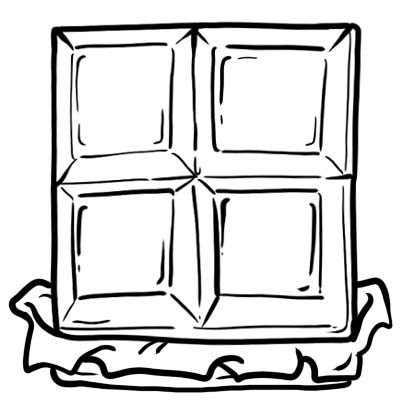
चॉकलेट का प्रत्येक भाग या क्यूब एक-चौथाई है यानी \(\frac{1}{4}\)
इसका मतलब है, एक पूरी चॉकलेट को चार बराबर भागों में बांटा गया है।
मान लीजिए, जैक ने चॉकलेट का अपना हिस्सा खा लिया, हम कह सकते हैं कि उसने चॉकलेट का एक-चौथाई या \(\frac{1}{4}\) खा लिया। अब कितनी चॉकलेट बची है? 3 भाग बचे हैं, इसलिए हम कह सकते हैं कि \(\frac{3}{4}\) या तीन-चौथाई चॉकलेट बची है।
नीचे दिए गए चित्र पर एक नज़र डालें,
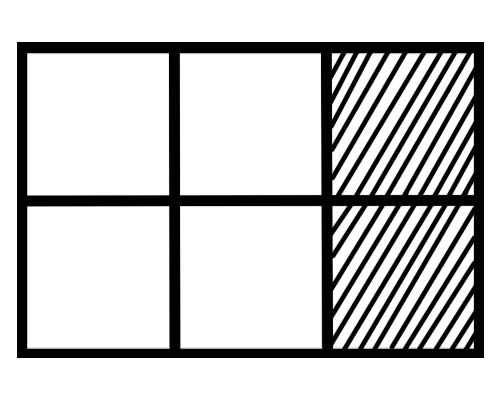
इस आकृति में प्रत्येक भाग का एक अंश क्या है? छह बराबर भाग हैं, इसलिए प्रत्येक भाग का एक अंश \(\frac{1}{6}\) ।
दी गई आकृति में पूरे के कितने भाग छायांकित हैं? कुल 6 भागों में से 2 भाग छायांकित हैं, इसलिए कुल भिन्न \(\frac{2}{6}\) ।
दी गई आकृति में पूरे के कितने भाग छायांकित नहीं हैं? कुल 6 भागों में से 4 भाग छायांकित नहीं हैं, इसलिए कुल अंश \(\frac{4}{6}\) ।
हम भिन्न का उपयोग समूह के किसी भाग को निरूपित करने के लिए भी कर सकते हैं। आइए एक कक्षा का उदाहरण लेते हैं जिसमें 12 छात्र हैं और कक्षा शिक्षक कक्षा को 2 समान समूहों में विभाजित करना चाहता है। प्रत्येक समूह में 6 विद्यार्थी होंगे। 12 का \(\frac{1}{2}\) 6 . है 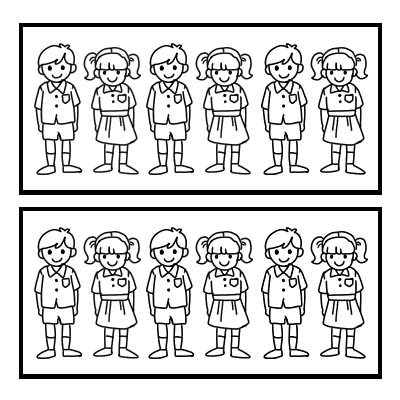
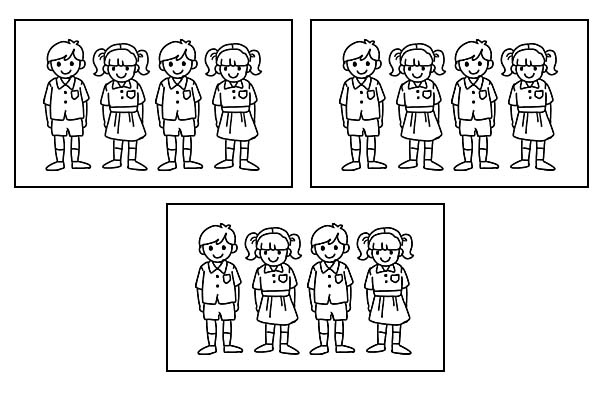
यदि एक ही कक्षा को 3 समान समूहों में विभाजित किया जाता है, तो प्रत्येक समूह में 4 छात्र होंगे। चूंकि 12 का \(\frac{1}{3}\) 4 है।
भिन्न भिन्न प्रकार के होते हैं जिनकी चर्चा नीचे की गई है:
उचित भिन्न
एक उचित भिन्न एक संख्या है जो पूर्ण के एक भाग का प्रतिनिधित्व करती है। एक उचित भिन्न में, हर में संख्या उन भागों की संख्या को दर्शाती है जिनमें पूर्ण विभाजित है, जबकि अंश में संख्या उन भागों की संख्या दर्शाती है जिन्हें लिया गया है। एक उचित भिन्न एक भिन्न है जो एक से कम है, जिसमें अंश हर से कम है।
उदाहरण के लिए,
\(\frac{2}{5}\) यानी कुल 5 भागों में से 2 भाग
\(\frac{3}{7}\) यानी कुल 7 भागों में से 3 भाग
अनुचित भिन्न
जिस भिन्न का अंश हर से बड़ा होता है उसे अनुचित भिन्न कहते हैं।
उदाहरण के लिए,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….आदि।
मिश्रित अंश
एक पूर्ण और एक भाग के संयोजन को मिश्रित भिन्न कहा जाता है।
उदाहरण के लिए,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...आदि।
एक अनुचित भिन्न का मिश्रित भिन्न में परिवर्तन
भागफल और शेष प्राप्त करने के लिए अनुचित भिन्न के हर द्वारा अंश को विभाजित करके एक अनुचित भिन्न को मिश्रित भिन्न के रूप में व्यक्त किया जा सकता है। तब मिश्रित भिन्न होगा
मिश्रित भिन्न = भागफल (शेष ∕ भाजक)
मिश्रित भिन्न का अनुचित भिन्न में परिवर्तन
मिश्रित भिन्न को अनुचित भिन्न के रूप में निम्न प्रकार से लिखकर लिखा जा सकता है:
[(संपूर्ण × हर) + अंश)] हर
भिन्नों की तरह
समान भाजक वाले भिन्नों को भिन्न कहा जाता है।
उदाहरण के लिए,
\(\frac{3}{10}\) , \(\frac{4}{10}\) और \(\frac{7}{10}\) भिन्नों की तरह हैं
भिन्नों के विपरीत
भिन्न हर वाले भिन्न भिन्न भिन्न कहलाते हैं।
उदाहरण के लिए,
\(\frac{3}{7}\) , \(\frac{5}{9}\) और \(\frac{2}{15}\) भिन्न भिन्न हैं
समतुल्य भाग
भिन्न जो पूर्ण के एक ही भाग का प्रतिनिधित्व करते हैं, तुल्य भिन्न कहलाते हैं।
उदाहरण के लिए,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
भिन्न का सरलतम रूप
एक भिन्न को उसके सरलतम रूप में या उसके निम्नतम रूप में कहा जाता है यदि उसके अंश और हर में एक को छोड़कर कोई सामान्य गुणनखंड न हो। किसी भिन्न का सबसे सरल रूप उसके अंश और हर को उसके उच्चतम सामान्य गुणनखंड (HCF) से विभाजित करके भी पाया जा सकता है। मान लीजिए, उपरोक्त उदाहरण में, पहला अंश \(\frac{1}{2}\) अपने सरलतम रूप में है क्योंकि 1 और 2 में एक को छोड़कर कोई उभयनिष्ठ गुणनखंड नहीं है; दूसरी भिन्न \(\frac{2}{4}\) अपने सरलतम रूप में नहीं है क्योंकि 2 और 4 के दो सामान्य गुणनखंड हैं - 1 और 2, यदि हम 2 और 4 को उच्चतम सामान्य गुणनखंड अर्थात 2 से विभाजित करते हैं तो \(\frac{2}{4}\) बन जाएगा \(\frac{1}{2}\) जो अब भिन्न का सबसे सरल रूप है।