Razlomak je dio cjeline. Potpuni ili puni objekt je cjelina. Cjelina može biti skupina objekata ili jedan objekt. Kada cijelu stvar podijelimo na jednake dijelove, tada se svaki dio naziva razlomak.
Na donjoj slici jedna puna jabuka podijeljena je na dvije polovice. Svaka polovica je razlomak predstavljen kao \(\frac{1}{2}\) gdje je 1 brojnik, a 2 nazivnik.

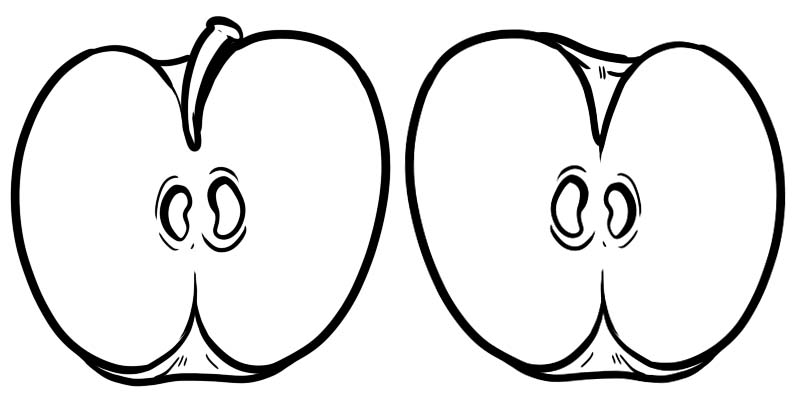
Razlomak se sastoji od dva broja koji su podijeljeni linijom.
Broj koji je napisan ispod crte poznat je kao nazivnik. Nazivnik pokazuje na koliko je jednakih dijelova nešto podijeljeno.
Broj koji je napisan iznad crte poznat je kao brojnik. Brojnik pokazuje koliko je dijelova cjeline uzeto.
Brojnik može biti veći ili manji od nazivnika.
Nazivnik NIJE jednak nuli ili jedan.
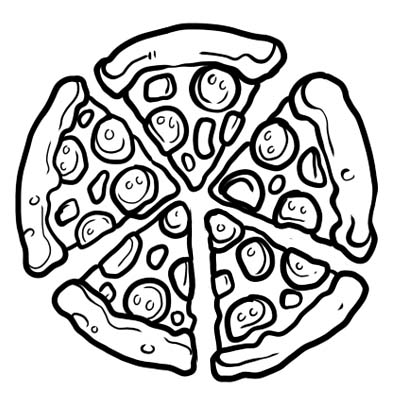
Pizza je podijeljena na pet jednakih dijelova. Ako pojedete samo jednu krišku pizze, to znači da ste pojeli \(\frac{1}{5}\) cijele pizze. \(\frac{1}{5}\) je ovdje razlomak.
Polovice i četvrtine
Harry i Jack bili su gladni. Kupili su kolačić. Podijelili su kolač tako što su ga podijelili na dva jednaka dijela:

Ovdje su 1. i 2. dio dva dijela kolača. Prvi dio je jedna polovica, a drugi dio je druga polovica.
Četvrtine (1/4) i tri četvrtine (3/4)
Harry, Jack, Sam i Oliver kupili su čokoladicu. Režu ga na 4 jednaka dijela.
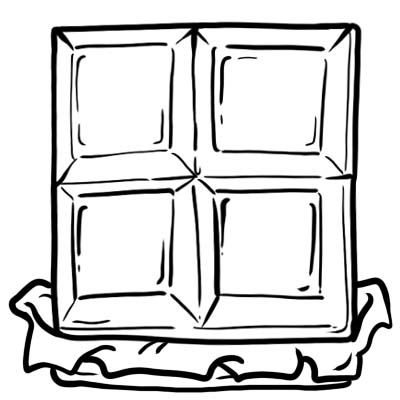
Svaki dio ili kocka čokolade je jedna četvrtina tj. \(\frac{1}{4}\)
To znači, jedna cijela čokolada podijeljena na četiri jednaka dijela.
Pretpostavimo da je Jack pojeo svoj dio čokolade, možemo reći da je pojeo jednu četvrtinu ili \(\frac{1}{4}\) čokolade. Koliko je čokolade sada ostalo? Ostala su 3 dijela, pa možemo reći da je ostalo \(\frac{3}{4}\) ili tri četvrtine čokolade.
Pogledajte dolje prikazanu sliku,
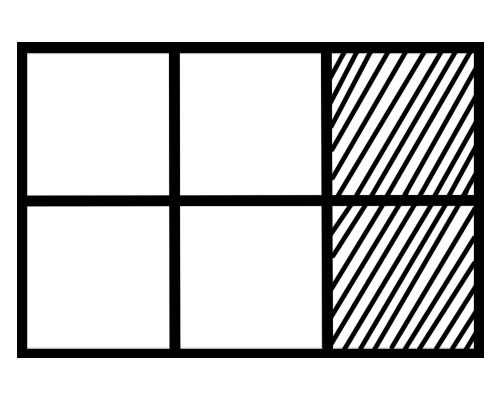
Koliki je dio svakog dijela na ovoj slici? Postoji šest jednakih dijelova, pa je razlomak svakog dijela \(\frac{1}{6}\) .
Koliko je dijelova cjeline zasjenjeno na danoj slici? 2 dijela od ukupno 6 dijelova su zasjenjena, tako da je ukupni razlomak \(\frac{2}{6}\) .
Koliko dijelova cjeline nije zasjenjeno na danoj slici? 4 dijela od ukupno 6 dijelova nisu zasjenjena, pa je ukupni razlomak \(\frac{4}{6}\) .
Također možemo koristiti razlomak za predstavljanje dijela grupe. Uzmimo primjer razreda koji ima 12 učenika, a razrednik želi podijeliti razred u 2 jednake grupe. Svaka grupa će imati 6 učenika. \(\frac{1}{2}\) od 12 je 6 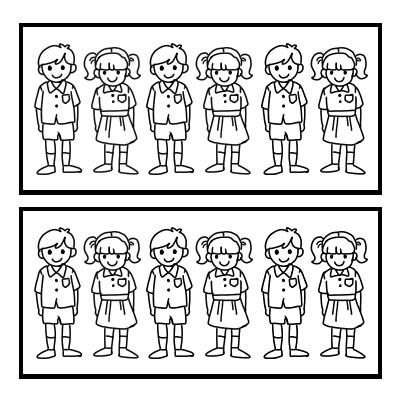
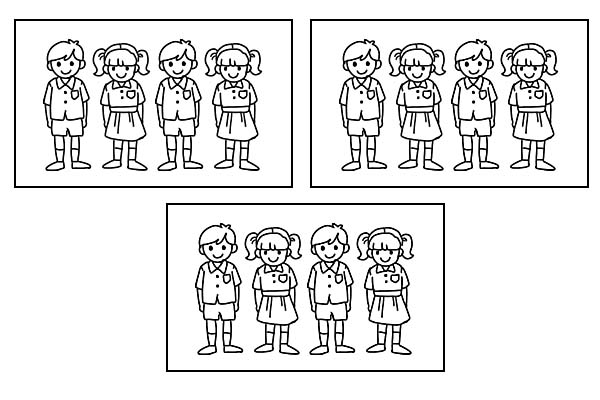
Ako je isti razred podijeljen u 3 jednake grupe, svaka grupa će imati 4 učenika. Kako je \(\frac{1}{3}\) od 12 4.
Postoje različite vrste razlomaka kao što je objašnjeno u nastavku:
Pravilni razlomci
Pravi razlomak je broj koji predstavlja dio cjeline. U pravilnom razlomku broj u nazivniku pokazuje broj dijelova na koje je podijeljena cjelina, dok broj u brojniku pokazuje broj dijelova koji su uzeti. Pravi razlomak je razlomak koji je manji od jedan, s brojnikom manjim od nazivnika.
Na primjer,
\(\frac{2}{5}\) tj. 2 dijela od ukupno 5 dijelova
\(\frac{3}{7}\) tj. 3 dijela od ukupno 7 dijelova
Nepravilni razlomci
Razlomak u kojem je brojnik veći od nazivnika naziva se nepravilan razlomak.
Na primjer,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….itd.
Mješovite frakcije
Kombinacija cjeline i dijela naziva se mješoviti razlomak.
Na primjer,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...itd.
Pretvorba nepravilnog razlomka u mješoviti razlomak
Nepravilan razlomak se može izraziti kao mješoviti razlomak dijeljenjem brojnika s nazivnikom nepravilnog razlomka kako bi se dobili kvocijent i ostatak. Tada će miješana frakcija biti
Mješoviti razlomak = količnik (ostatak ∕ djelitelj)
Pretvorba mješovitog razlomka u nepravilan razlomak
Mješoviti razlomak se može napisati u obliku nepravilnog razlomka na sljedeći način:
[(Cijeli × nazivnik) + brojnik)] ∕ Nazivnik
Kao razlomci
Za razlomke s istim nazivnikom kaže se da su kao razlomci.
Na primjer,
\(\frac{3}{10}\) , \(\frac{4}{10}\) i \(\frac{7}{10}\) su poput razlomaka
Za razliku od razlomaka
Za razlomke s različitim nazivnicima kaže se da su različiti od razlomaka.
Na primjer,
\(\frac{3}{7}\) , \(\frac{5}{9}\) i \(\frac{2}{15}\) nisu slični razlomcima
Ekvivalentni razlomci
Za razlomke koji predstavljaju isti dio cjeline kaže se da su ekvivalentni razlomci.
Na primjer,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Najjednostavniji oblik razlomka
Za razlomak se kaže da je u svom najjednostavnijem ili najnižem obliku ako njegov brojnik i nazivnik nemaju zajednički faktor osim jednog. Najjednostavniji oblik razlomka također se može pronaći dijeljenjem brojnika i nazivnika s najvećim zajedničkim faktorom (HCF). Recimo, u gornjem primjeru, prvi razlomak \(\frac{1}{2}\) je u svom najjednostavnijem obliku jer 1 i 2 nemaju zajednički faktor osim jednog; drugi razlomak \(\frac{2}{4}\) nije u svom najjednostavnijem obliku jer 2 i 4 imaju dva zajednička faktora – 1 i 2, ako podijelimo 2 i 4 s najvišim zajedničkim faktorom, tj. 2, tada \(\frac{2}{4}\) će postati \(\frac{1}{2}\) što je sada najjednostavniji oblik razlomka.