Pecahan adalah bagian dari keseluruhan. Objek yang lengkap atau penuh adalah keseluruhan. Keseluruhan dapat berupa sekelompok objek atau objek tunggal. Ketika kita membagi keseluruhan menjadi bagian yang sama, maka setiap bagian disebut pecahan.
Pada gambar di bawah, satu apel utuh dibagi menjadi dua bagian. Setiap setengah adalah pecahan yang direpresentasikan sebagai \(\frac{1}{2}\) di mana 1 adalah pembilangnya dan 2 adalah penyebutnya.

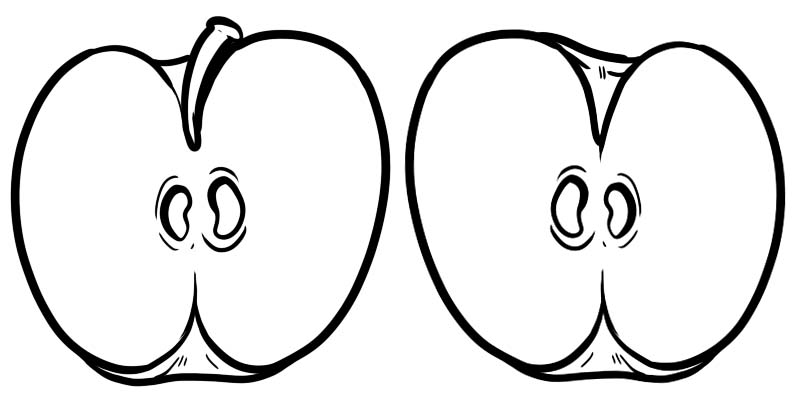
Pecahan terdiri dari dua bilangan yang dipisahkan oleh garis.
Angka yang ditulis di bawah garis disebut penyebut. Penyebut menunjukkan berapa banyak bagian yang sama dari sesuatu yang telah dibagi.
Angka yang ditulis di atas garis disebut pembilang. Pembilang menunjukkan berapa banyak bagian dari keseluruhan yang diambil.
Pembilangnya bisa lebih besar atau lebih kecil dari penyebutnya.
Penyebutnya TIDAK sama dengan nol atau satu.
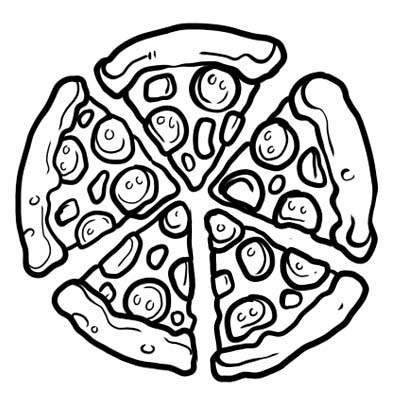
Sebuah pizza dibagi menjadi lima bagian yang sama. Jika Anda makan hanya satu potong pizza, artinya Anda makan \(\frac{1}{5}\) seluruh pizza. \(\frac{1}{5}\) adalah pecahan di sini.
Separuh dan Seperempat
Harry dan Jack lapar. Mereka membeli kue mangkuk. Mereka membagi cupcake dengan membaginya menjadi dua bagian yang sama:

Di sini, Bagian 1 dan Bagian 2 adalah dua pecahan cupcake. Bagian 1 adalah satu setengah dan Bagian 2 adalah setengah lainnya.
Kuartal (1/4) dan Tiga Kuartal (3/4)
Harry, Jack, Sam, dan Oliver membeli sebatang cokelat. Mereka memotongnya menjadi 4 bagian yang sama.
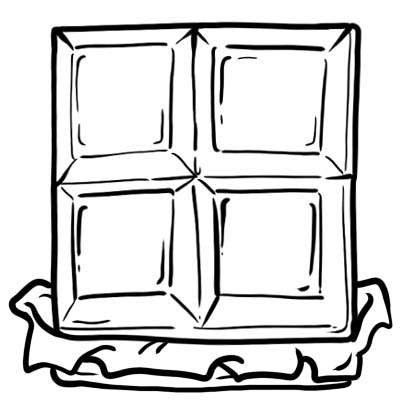
Setiap bagian atau kubus coklat adalah seperempat yaitu \(\frac{1}{4}\)
Artinya, satu coklat utuh dibagi menjadi empat bagian yang sama.
Misalkan, Jack memakan bagian cokelatnya, kita dapat mengatakan dia memakan seperempat atau \(\frac{1}{4}\) cokelat. Berapa banyak coklat yang tersisa sekarang? 3 bagian tersisa, jadi kita dapat mengatakan bahwa \(\frac{3}{4}\) atau tiga perempat cokelat tersisa.
Perhatikan gambar di bawah ini,
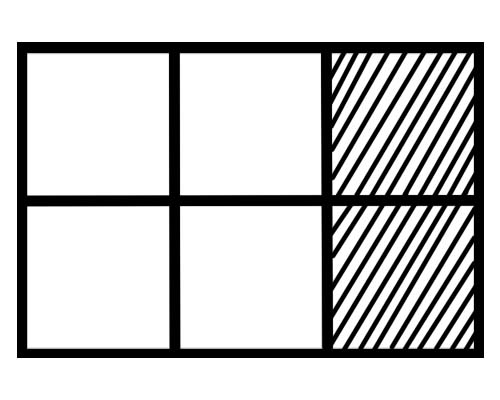
Berapakah pecahan dari setiap bagian pada gambar ini? Ada enam bagian yang sama, jadi pecahan dari setiap bagian adalah \(\frac{1}{6}\) .
Berapa banyak bagian dari keseluruhan yang diarsir pada gambar yang diberikan? 2 bagian dari total 6 bagian diarsir, sehingga pecahan totalnya adalah \(\frac{2}{6}\) .
Berapa banyak bagian dari keseluruhan yang tidak diarsir pada gambar yang diberikan? 4 bagian dari total 6 bagian tidak diarsir, jadi pecahan totalnya adalah \(\frac{4}{6}\) .
Kita juga dapat menggunakan pecahan untuk mewakili bagian dari grup. Mari kita ambil contoh kelas yang memiliki 12 siswa dan guru kelas ingin membagi kelas menjadi 2 kelompok yang sama. Setiap kelompok akan memiliki 6 siswa. \(\frac{1}{2}\) dari 12 adalah 6 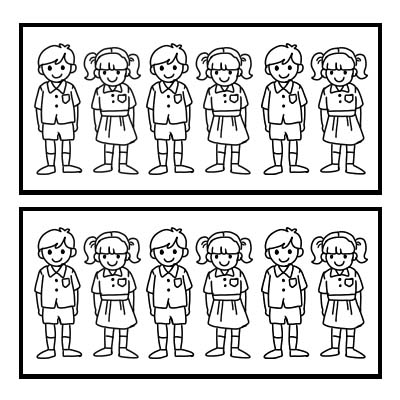
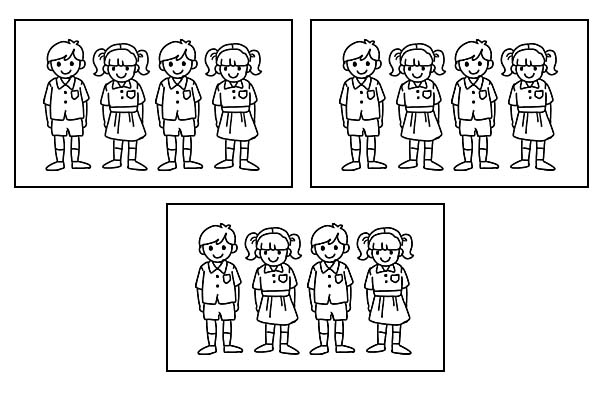
Jika kelas yang sama dibagi menjadi 3 kelompok yang sama, setiap kelompok akan memiliki 4 siswa. Karena \(\frac{1}{3}\) dari 12 adalah 4.
Ada berbagai jenis pecahan seperti yang dibahas di bawah ini:
Pecahan yang tepat
Pecahan yang tepat adalah angka yang mewakili bagian dari keseluruhan. Dalam pecahan biasa, angka pada penyebut menunjukkan jumlah bagian yang dibagi seluruhnya, sedangkan angka pada pembilang menunjukkan jumlah bagian yang diambil. Pecahan biasa adalah pecahan yang kurang dari satu, dengan pembilangnya lebih kecil dari penyebutnya.
Misalnya,
\(\frac{2}{5}\) yaitu 2 bagian dari total 5 bagian
\(\frac{3}{7}\) yaitu 3 bagian dari total 7 bagian
Pecahan yang tidak benar
Pecahan yang pembilangnya lebih besar dari penyebutnya disebut pecahan biasa.
Misalnya,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….dst.
Pecahan campuran
Gabungan dari keseluruhan dan sebagian disebut pecahan campuran.
Misalnya,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...dst.
Konversi pecahan biasa menjadi pecahan campuran
Pecahan tidak wajar dapat dinyatakan sebagai pecahan campuran dengan membagi pembilang dengan penyebut pecahan biasa untuk mendapatkan hasil bagi dan sisanya. Maka pecahan campuran akan menjadi
Pecahan Campuran = Hasil Bagi (Sisa ∕ Pembagi)
Konversi pecahan campuran menjadi pecahan biasa
Pecahan campuran dapat ditulis dalam bentuk pecahan biasa dengan menuliskannya sebagai berikut:
[(Seluruh × Penyebut) + Pembilang)] ∕ Penyebut
Seperti pecahan
Pecahan dengan penyebut yang sama dikatakan seperti pecahan.
Misalnya,
\(\frac{3}{10}\) , \(\frac{4}{10}\) dan \(\frac{7}{10}\) seperti pecahan
Berbeda dengan pecahan
Pecahan dengan penyebut berbeda dikatakan sebagai pecahan tak sejenis.
Misalnya,
\(\frac{3}{7}\) , \(\frac{5}{9}\) dan \(\frac{2}{15}\) tidak seperti pecahan
pecahan setara
Pecahan yang mewakili bagian yang sama dari keseluruhan dikatakan pecahan setara.
Misalnya,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Bentuk pecahan paling sederhana
Pecahan dikatakan dalam bentuk paling sederhana atau bentuk terendah jika pembilang dan penyebutnya tidak memiliki faktor persekutuan kecuali satu. Bentuk pecahan paling sederhana juga dapat ditemukan dengan membagi pembilang dan penyebutnya dengan faktor persekutuan tertinggi (HCF). Misalnya, dalam contoh di atas, pecahan pertama \(\frac{1}{2}\) berada dalam bentuk paling sederhana karena 1 dan 2 tidak memiliki faktor persekutuan kecuali satu; pecahan kedua \(\frac{2}{4}\) bukan bentuk paling sederhana karena 2 dan 4 memiliki dua faktor persekutuan – 1 dan 2, jika kita membagi 2 dan 4 dengan faktor persekutuan tertinggi yaitu 2 maka \(\frac{2}{4}\) akan menjadi \(\frac{1}{2}\) yang sekarang menjadi bentuk pecahan paling sederhana.