Una frazione è una parte di un tutto. Un oggetto completo o completo è un tutto. Un intero può essere un gruppo di oggetti o un singolo oggetto. Quando dividiamo una cosa intera in parti uguali, ogni parte si chiama frazione.
Nell'immagine sottostante, una mela intera è divisa in due metà. Ogni metà è una frazione rappresentata come \(\frac{1}{2}\) dove 1 è il numeratore e 2 è il denominatore.

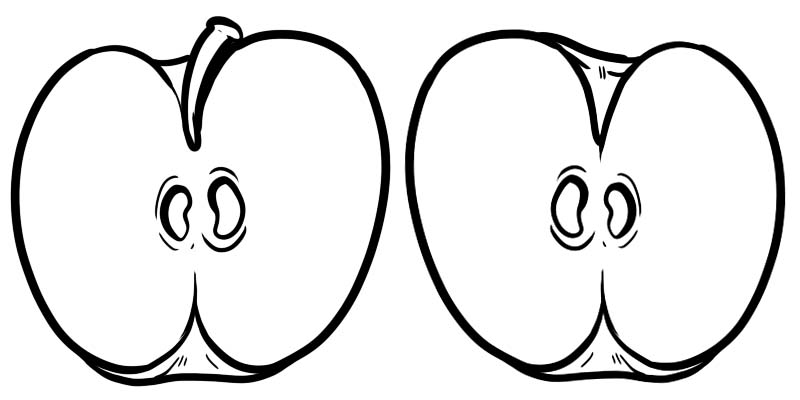
Una frazione è composta da due numeri divisi da una linea.
Il numero che è scritto sotto la riga è noto come denominatore. Il denominatore mostra in quante parti uguali è stato suddiviso qualcosa.
Il numero che è scritto sopra la riga è noto come numeratore. Il numeratore mostra quante parti del tutto sono prese.
Il numeratore può essere maggiore o minore del denominatore.
Il denominatore NON è uguale a zero o uno.
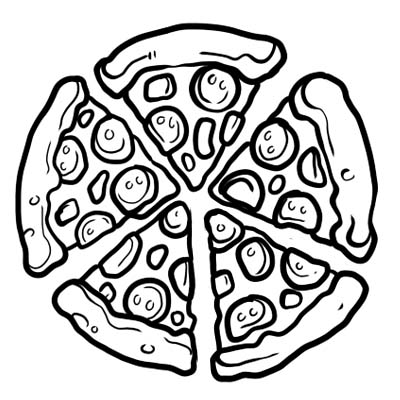
Una pizza è divisa in cinque parti uguali. Se mangi solo una fetta di pizza, significa che hai mangiato \(\frac{1}{5}\) dell'intera pizza. \(\frac{1}{5}\) è la frazione qui.
Metà e Quarti
Harry e Jack avevano fame. Hanno comprato un cupcake. Hanno condiviso il cupcake dividendolo in due parti uguali:

Qui, la Parte 1 e la Parte 2 sono due frazioni del cupcake. La parte 1 è metà e la parte 2 è un'altra metà.
Quarti (1/4) e Tre quarti (3/4)
Harry, Jack, Sam e Oliver hanno comprato una tavoletta di cioccolato. Lo tagliano in 4 parti uguali.
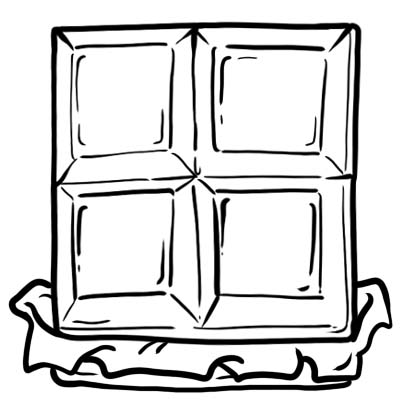
Ogni parte o cubetto di cioccolato è un quarto cioè \(\frac{1}{4}\)
Ciò significa, un intero cioccolato diviso in quattro parti uguali.
Supponiamo che Jack abbia mangiato la sua parte di cioccolato, possiamo dire che ha mangiato un quarto o \(\frac{1}{4}\) del cioccolato. Quanto cioccolato è rimasto adesso? Sono rimaste 3 parti, quindi possiamo dire che sono rimasti \(\frac{3}{4}\) o tre quarti di cioccolato.
Dai un'occhiata alla figura riportata di seguito,
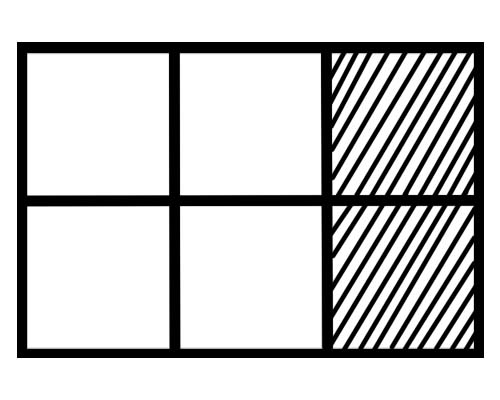
Qual è una frazione di ogni parte in questa figura? Ci sono sei parti uguali, quindi una frazione di ogni parte è \(\frac{1}{6}\) .
Quante parti del tutto sono ombreggiate nella figura data? 2 parti delle 6 parti totali sono ombreggiate, quindi la frazione totale è \(\frac{2}{6}\) .
Quante parti del tutto non sono ombreggiate nella figura data? 4 parti delle 6 parti totali non sono ombreggiate, quindi la frazione totale è \(\frac{4}{6}\) .
Possiamo anche usare una frazione per rappresentare una parte di un gruppo. Facciamo un esempio di una classe con 12 studenti e l'insegnante di classe vuole dividere la classe in 2 gruppi uguali. Ogni gruppo avrà 6 studenti. \(\frac{1}{2}\) di 12 è 6 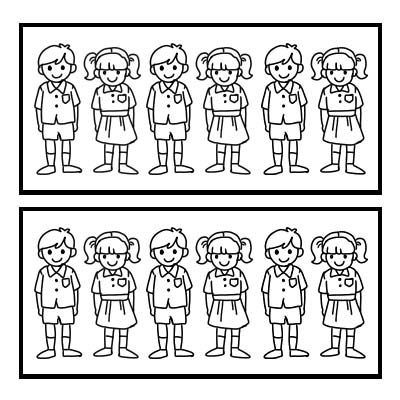
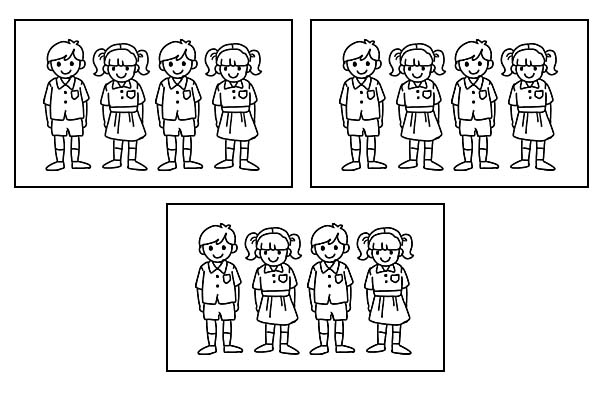
Se la stessa classe è divisa in 3 gruppi uguali, ogni gruppo avrà 4 studenti. Poiché \(\frac{1}{3}\) di 12 è 4.
Esistono diversi tipi di frazioni come discusso di seguito:
Frazioni proprie
Una frazione propria è un numero che rappresenta una parte di un intero. In una frazione propria, il numero al denominatore mostra il numero di parti in cui è diviso il tutto, mentre il numero al numeratore mostra il numero di parti che sono state prese. Una frazione propria è una frazione minore di uno, con il numeratore minore del denominatore.
Per esempio,
\(\frac{2}{5}\) cioè 2 parti su un totale di 5 parti
\(\frac{3}{7}\) cioè 3 parti su un totale di 7 parti
Frazioni improprie
Una frazione in cui il numeratore è maggiore del denominatore si chiama frazione impropria.
Per esempio,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….ecc.
Frazioni miste
Una combinazione di un intero e di una parte si chiama frazione mista.
Per esempio,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...ecc.
Conversione di una frazione impropria in una frazione mista
Una frazione impropria può essere espressa come frazione mista dividendo il numeratore per il denominatore della frazione impropria per ottenere il quoziente e il resto. Quindi la frazione mista sarà
Frazione mista = Quoziente (Resto ∕ Divisore)
Conversione di una frazione mista in una frazione impropria
Una frazione mista può essere scritta sotto forma di frazione impropria scrivendola nel modo seguente:
[(Intero × Denominatore) + Numeratore)] ∕ Denominatore
Come le frazioni
Le frazioni con lo stesso denominatore si dicono come frazioni.
Per esempio,
\(\frac{3}{10}\) , \(\frac{4}{10}\) e \(\frac{7}{10}\) sono come frazioni
A differenza delle frazioni
Le frazioni con denominatori diversi si dicono diverse dalle frazioni.
Per esempio,
\(\frac{3}{7}\) , \(\frac{5}{9}\) e \(\frac{2}{15}\) sono frazioni diverse
Frazioni equivalenti
Le frazioni che rappresentano la stessa parte di un intero si dicono frazioni equivalenti.
Per esempio,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
La forma più semplice di una frazione
Si dice che una frazione sia nella sua forma più semplice o nella sua forma più bassa se il numeratore e il denominatore non hanno divisori comuni tranne uno. La forma più semplice di una frazione può anche essere trovata dividendo il suo numeratore e denominatore per il suo massimo comune divisore (HCF). Supponiamo che, nell'esempio precedente, la prima frazione \(\frac{1}{2}\) sia nella sua forma più semplice poiché 1 e 2 non hanno divisori comuni tranne uno; la seconda frazione \(\frac{2}{4}\) non è nella sua forma più semplice perché 2 e 4 hanno due divisori in comune – 1 e 2, se dividiamo 2 e 4 per il massimo comune divisore cioè 2 allora \(\frac{2}{4}\) diventerà \(\frac{1}{2}\) che ora è la forma più semplice della frazione.