分数は全体の一部です。完全または完全なオブジェクトは全体です。全体は、オブジェクトのグループまたは単一のオブジェクトの場合があります。全体を等分すると、それぞれの部分は分数と呼ばれます。
下の画像では、1 つの完全なリンゴが 2 つの半分に分割されています。各半分は\(\frac{1}{2}\)として表される分数で、1 は分子、2 は分母です。

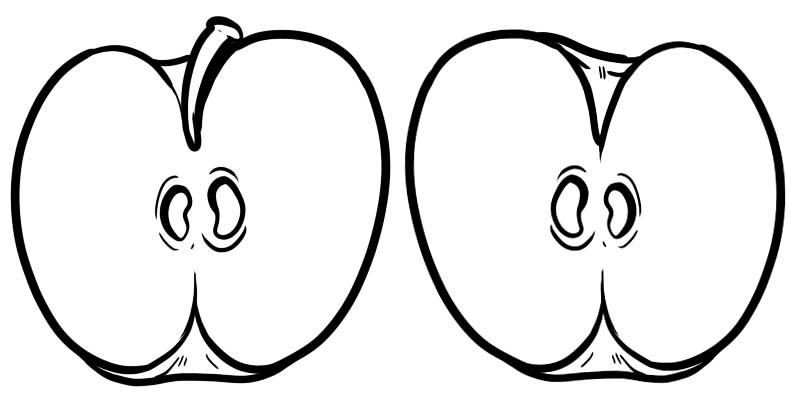
分数は、2 つの数を線で割ったものです。
線の下に書かれている数字は、分母として知られています。分母は、何かが何等分されたかを示します。
線の上に書かれた数字は、分子として知られています。分子は、全体のいくつの部分が取られるかを示します。
分子は分母より大きくても小さくてもかまいません。
分母はゼロまたは 1 に等しくありません。
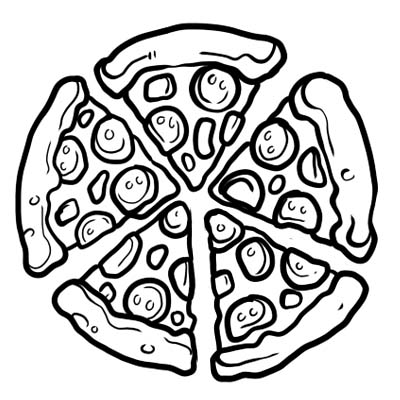
ピザは 5 等分されます。ピザを 1 切れだけ食べた場合は、ピザ全体を\(\frac{1}{5}\)食べたことになります。 \(\frac{1}{5}\)分数です。
半分と四分の一
ハリーとジャックはお腹がすいた。彼らはカップケーキを買いました。彼らはカップケーキを 2 つの等しい部分に分けて分けました。

ここで、パート 1 とパート 2 はカップケーキの 2 つの部分です。パート 1 は半分で、パート 2 は別の半分です。
4 分の 1 (1/4) と 4 分の 3 (3/4)
ハリー、ジャック、サム、オリバーはチョコレートバーを買いました。彼らはそれを 4 等分に切りました。
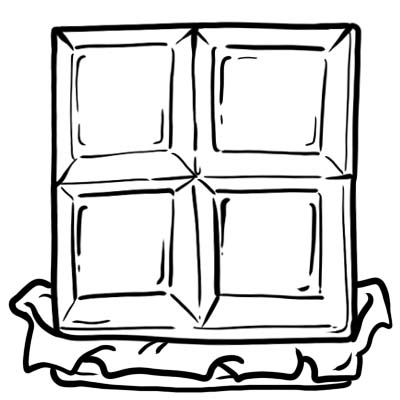
チョコレートの各部分または立方体は 4 分の 1、つまり\(\frac{1}{4}\)
これは、1 つのチョコレート全体を 4 つの等しい部分に分割することを意味します。
ジャックが自分の分量のチョコレートを食べたと仮定すると、彼はチョコレートの 4 分の 1 または\(\frac{1}{4}\)を食べたと言えます。チョコレートは今どれくらい残っていますか? 3 個残っているので、 \(\frac{3}{4}\)または 4 分の 3 のチョコレートが残っていると言えます。
下の図を見てください。
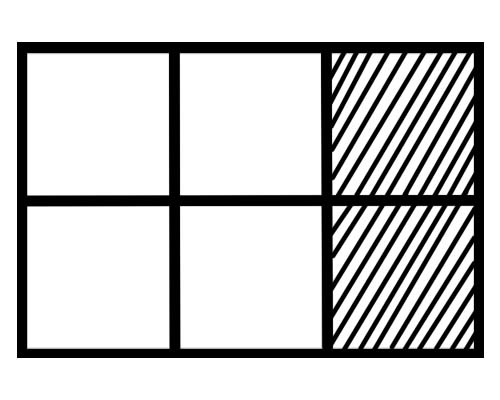
この図の各部分の分数は? 6 つの等しい部分があるため、各部分の分数は\(\frac{1}{6}\)です。
与えられた図で、全体の何個の部分が陰になっていますか?全部で 6 つの部分のうち 2 つの部分が陰になっているため、分数の合計は\(\frac{2}{6}\)になります。
与えられた図で、全体の何個の部分が影で覆われていませんか?合計 6 つの部分のうち 4 つの部分が陰影を付けられていないため、分数の合計は\(\frac{4}{6}\)になります。
分数を使用してグループの一部を表すこともできます。 12 人の生徒がいるクラスの例を見てみましょう。クラスの教師は、クラスを 2 つの等しいグループに分けたいと考えています。各グループには6人の学生がいます。 \(\frac{1}{2}\) /12 は 6 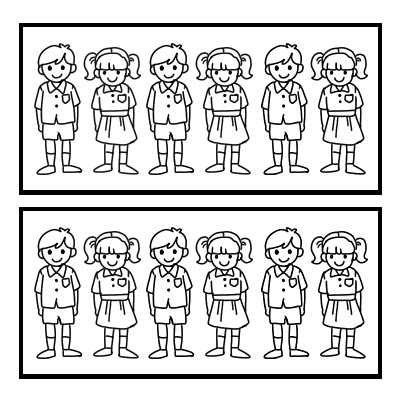
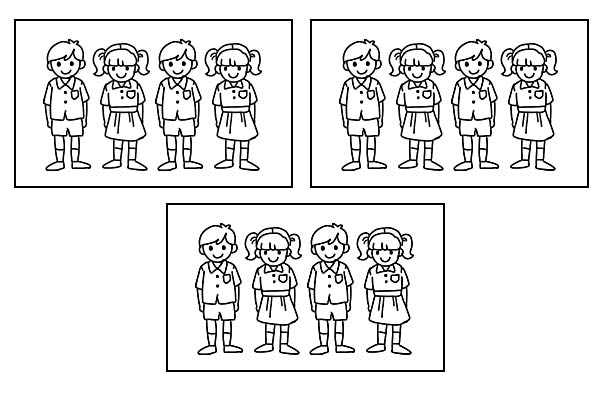
同じクラスを 3 つのグループに分けた場合、各グループには 4 人の生徒が含まれます。 \(\frac{1}{3}\)の 12 は 4 です。
以下で説明するように、分数にはさまざまな種類があります。
適切な分数
固有分数は、全体の一部を表す数です。適切な分数では、分母の数字は全体を分割した部分の数を示し、分子の数字は分割された部分の数を示します。固有分数とは、分子が分母よりも小さい、1 未満の分数です。
例えば、
\(\frac{2}{5}\)つまり、合計 5 つの部分のうちの 2 つの部分
\(\frac{3}{7}\)つまり、合計 7 つの部分のうちの 3 つの部分
不適切な分数
分子が分母よりも大きい分数を仮分数といいます。
例えば、
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) …など。
混合分数
全体と一部を合わせたものを混合分数といいます。
例えば、
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...など。
仮分数の帯分数への変換
仮分数は、分子を仮分数の分母で割り、商と余りを求めることにより、帯分数として表すことができます。すると混合分数は
混合分数 = 商 (剰余 ∕ 除数)
混合分数の仮分数への変換
帯分数は、次のように書くと仮分数の形で書くことができます。
[(全体 × 分母) + 分子)] ∕ 分母
分数のように
分母が同じ分数を分数に似ているという。
例えば、
\(\frac{3}{10}\) 、 \(\frac{4}{10}\)および\(\frac{7}{10}\)は分数のようなものです
分数とは異なり
分母が異なる分数は、異なる分数であると言われます。
例えば、
\(\frac{3}{7}\) 、 \(\frac{5}{9}\)および\(\frac{2}{15}\)は分数とは異なります
同等の分数
全体の同じ部分を表す分数は、等価分数と呼ばれます。
例えば、
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
分数の最も単純な形
分数は、分子と分母に 1 つを除いて共通の約数がない場合、最も単純な形式または最小形式であると言われます。分数の最も単純な形式は、分子と分母を最大公約数 (HCF) で割ることによっても求められます。上記の例で、最初の分数\(\frac{1}{2}\) 1 と 2 には 1 つを除いて公約数がないため、最も単純な形式になっているとします。 2 番目の分数\(\frac{2}{4}\)最も単純な形式ではありません。これは、2 と 4 には 1 と 2 という 2 つの公約数があるためです\(\frac{2}{4}\) \(\frac{1}{2}\)になり、これが分数の最も単純な形になります。