Дропка е дел од целина. Целосен или целосен објект е целина. Целина може да биде група предмети или еден објект. Кога една целина делиме на еднакви делови, тогаш секој дел се нарекува дропка.
На сликата подолу, едно полно јаболко е поделено на две половини. Секоја половина е дропка претставена како \(\frac{1}{2}\) каде што 1 е броител, а 2 е именителот.

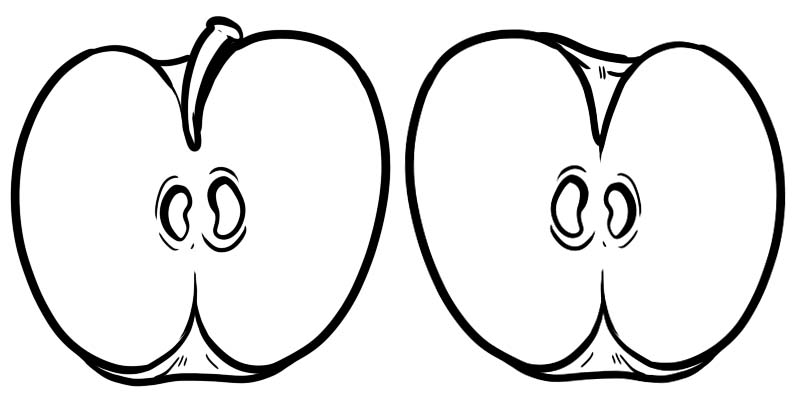
Дропката е составена од два броја кои се делат со права.
Бројот што е запишан под линијата е познат како именител. Именителот покажува на колку еднакви делови е поделено нешто.
Бројот што е напишан над линијата е познат како броител. Бројачот покажува колку делови од целината се земени.
Бројачот може да биде поголем или помал од именителот.
Именителот НЕ е еднаков на нула или еден.
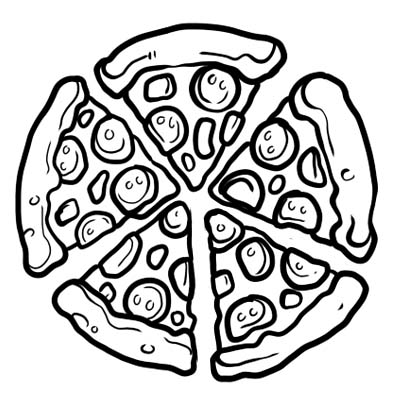
Пицата се дели на пет еднакви делови. Ако јадете само едно парче од пицата, тоа значи дека сте јаделе \(\frac{1}{5}\) од целата пица. \(\frac{1}{5}\) е дропката овде.
Половини и четвртини
Хари и Џек беа гладни. Купиле кекс. Тие го поделиле кексот делејќи го на два еднакви дела:

Овде, Дел 1 и Дел 2 се две фракции од кексот. Дел 1 е една половина и Дел 2 е друга половина.
Четвртини (1/4) и три четвртини (3/4)
Хари, Џек, Сем и Оливер купија чоколадо. Ја сечат на 4 еднакви делови.
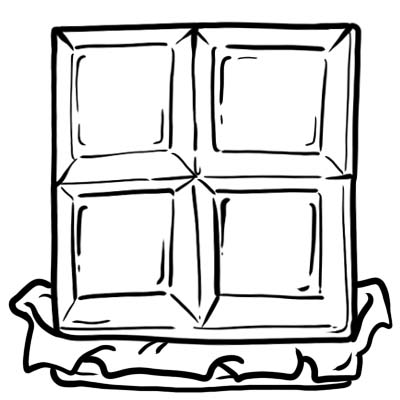
Секој дел или коцка чоколадо е една четвртина т.е. \(\frac{1}{4}\)
Тоа значи, едно цело чоколадо поделено на четири еднакви делови.
Да претпоставиме дека Џек го изел својот дел од чоколадото, можеме да кажеме дека изел една четвртина или \(\frac{1}{4}\) од чоколадото. Колку чоколадо остана сега? Останати се 3 дела, па можеме да кажеме дека остана \(\frac{3}{4}\) или три четвртини од чоколадото.
Погледнете ја сликата дадена подолу,
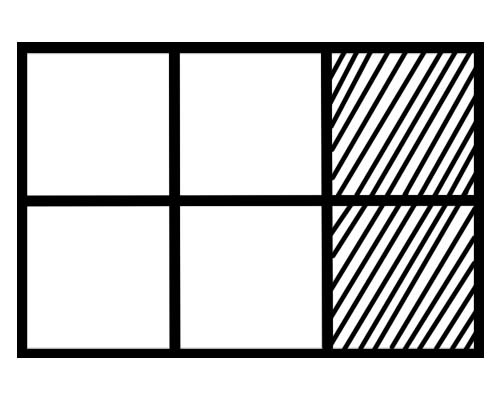
Колку е дропка од секој дел на оваа слика? Има шест еднакви делови, така што дропка од секој дел е \(\frac{1}{6}\) .
Колку делови од целината се засенчени на дадената слика? 2 дела од вкупно 6 дела се засенчени, така што вкупната дропка е \(\frac{2}{6}\) .
Колку делови од целината не се засенчени на дадената слика? 4 делови од вкупно 6 делови не се засенчени, така што вкупната дропка е \(\frac{4}{6}\) .
Можеме да користиме и дропка за да претставиме дел од група. Да земеме пример за паралелка со 12 ученици и класниот раководител сака да го подели часот во 2 еднакви групи. Секоја група ќе има по 6 ученици. \(\frac{1}{2}\) од 12 е 6 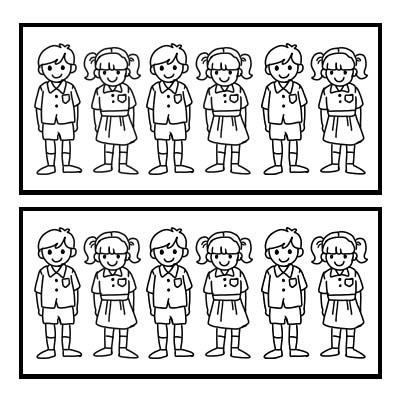
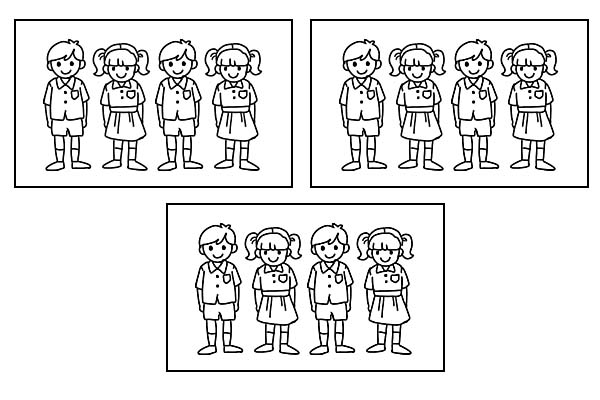
Доколку истиот клас е поделен во 3 еднакви групи, секоја група ќе има по 4 ученици. Бидејќи \(\frac{1}{3}\) од 12 е 4.
Постојат различни типови на дропки како што е дискутирано подолу:
Правилни дропки
Правилна дропка е број што претставува дел од целина. Во правилна дропка, бројот во именителот го покажува бројот на делови на кои е поделена целината, додека бројот во броителот го покажува бројот на делови што се земени. Правилна дропка е дропка што е помала од една, со броител помал од именителот.
На пример,
\(\frac{2}{5}\) односно 2 дела од вкупно 5 делови
\(\frac{3}{7}\) односно 3 дела од вкупно 7 делови
Несоодветни дропки
Дропката во која броителот е поголем од именителот се нарекува неправилна дропка.
На пример,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) … итн.
Мешани фракции
Комбинацијата од целина и дел се нарекува мешана дропка.
На пример,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ... итн.
Претворање на неправилна дропка во мешана дропка
Неправилна дропка може да се изрази како мешана дропка со делење на броителот со именителот на неправилната дропка за да се добие количникот и остатокот. Тогаш измешаната фракција ќе биде
Мешана дропка = количник (остаток ∕ делител)
Претворање на мешана дропка во неправилна дропка
Мешаната дропка може да се запише во форма на неправилна дропка со тоа што ќе ја запишете на следниов начин:
[(Цело × именител) + броител)] ∕ Именител
Како дропки
За дропките со ист именител се вели дека се како дропки.
На пример,
\(\frac{3}{10}\) , \(\frac{4}{10}\) и \(\frac{7}{10}\) се како дропки
За разлика од дропките
За дропките со различни именители се вели дека не се слични на дропките.
На пример,
\(\frac{3}{7}\) , \(\frac{5}{9}\) и \(\frac{2}{15}\) се за разлика од дропките
Еквивалентни дропки
Дропките што претставуваат ист дел од целината се вели дека се еквивалентни дропки.
На пример,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Наједноставниот облик на дропка
За дропка се вели дека е во наједноставна или најниска форма ако нејзиниот броител и именителот немаат заеднички фактор освен еден. Наједноставниот облик на дропка може да се најде и со делење на неговиот броител и именител со неговиот највисок заеднички фактор (HCF). Да речеме, во горниот пример, првата дропка \(\frac{1}{2}\) е во наједноставна форма бидејќи 1 и 2 немаат заеднички фактор освен еден; втората дропка \(\frac{2}{4}\) не е во наједноставна форма бидејќи 2 и 4 имаат два заеднички фактора - 1 и 2, ако ги поделиме 2 и 4 со највисокиот заеднички фактор т.е. 2 тогаш \(\frac{2}{4}\) ќе стане \(\frac{1}{2}\) што сега е наједноставната форма на дропката.