Бутархай нь бүхэл зүйлийн нэг хэсэг юм. Бүрэн эсвэл бүрэн объект нь бүхэл юм. Бүхэл нь бүлэг объект эсвэл нэг объект байж болно. Бид бүхэл зүйлийг тэнцүү хэсгүүдэд хуваавал хэсэг бүрийг бутархай гэж нэрлэдэг.
Доорх зурган дээр нэг бүтэн алимыг хоёр хэсэгт хуваасан байна. Хагас бүр нь \(\frac{1}{2}\) хэлбэрээр илэрхийлэгдэх бутархай бөгөөд 1 нь тоологч, 2 нь хуваагч юм.

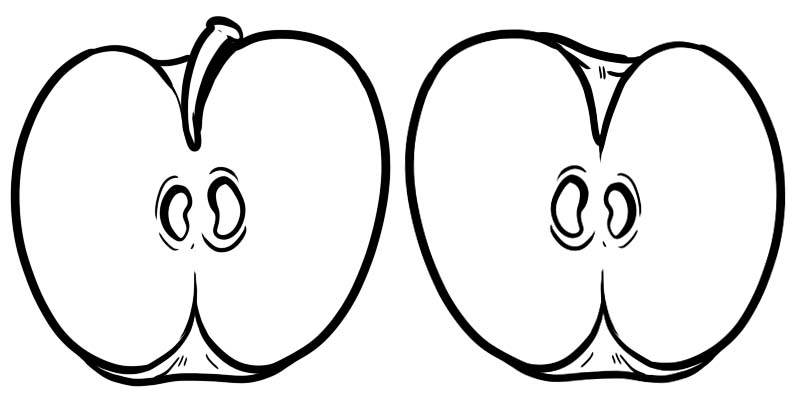
Бутархай нь шулуунаар хуваагдсан хоёр тооноос бүрдэнэ.
Мөрний доор бичигдсэн тоог хуваагч гэж нэрлэдэг. Хуваагч нь ямар нэг зүйл хэдэн тэнцүү хэсэгт хуваагдсаныг харуулдаг.
Мөрний дээгүүр бичигдсэн тоог тоологч гэж нэрлэдэг. Тоолуур нь бүхэл бүтэн хэдэн хэсгийг авсныг харуулж байна.
Тоолуур нь хуваагчаас их эсвэл бага байж болно.
Хуваагч нь тэг эсвэл нэгтэй тэнцүү биш.
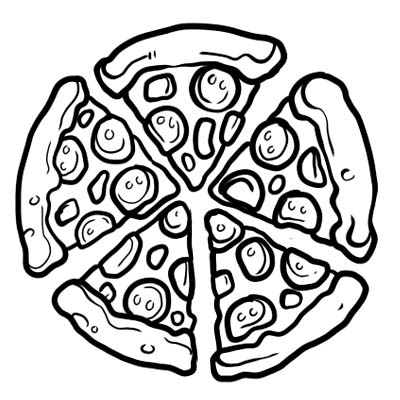
Пицца таван тэнцүү хэсэгт хуваагдана. Хэрэв та зөвхөн нэг зүсэм пицца идсэн бол энэ нь та бүх пиццаны \(\frac{1}{5}\) идсэн гэсэн үг юм. \(\frac{1}{5}\) нь энд байгаа бутархай юм.
Хагас ба дөрөвний нэг
Харри Жак хоёр өлсөж байлаа. Тэд аяга бялуу худалдаж авав. Тэд аяга бялууг хоёр тэнцүү хэсэгт хувааж хувааж авав.

Энд 1-р хэсэг ба 2-р хэсэг нь аяга бялууны хоёр хэсэг юм. 1-р хэсэг нь хагас, 2-р хэсэг нь өөр хагас юм.
Дөрөвний хэсэг (1/4) ба дөрөвний гурав (3/4)
Харри, Жэк, Сэм, Оливер гурав нэг шоколад худалдаж авав. Тэд үүнийг 4 тэнцүү хэсэгт хуваасан.
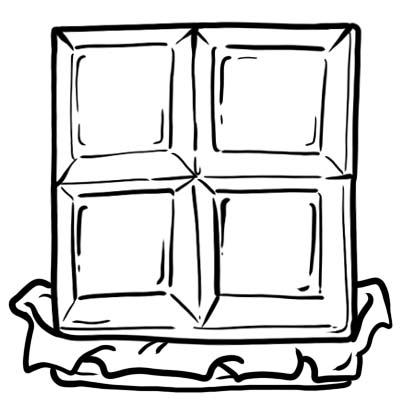
Шоколадны хэсэг буюу шоо бүр нь дөрөвний нэг буюу \(\frac{1}{4}\)
Энэ нь нэг шоколадыг дөрвөн тэнцүү хэсэгт хуваасан гэсэн үг юм.
Жак шоколадныхаа хэсгийг идсэн гэж бодъё, тэр шоколадны дөрөвний нэг буюу \(\frac{1}{4}\) идсэн гэж хэлж болно. Одоо хэр их шоколад үлдсэн бэ? 3 хэсэг үлдсэн тул \(\frac{3}{4}\) буюу шоколадны дөрөвний гурав үлдсэн гэж хэлж болно.
Доорх зургийг харна уу,
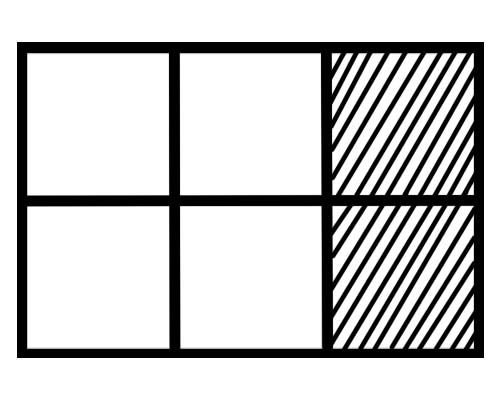
Энэ зураг дээрх хэсэг бүрийн хэдэн хэсэг вэ? Зургаан тэнцүү хэсэгтэй тул хэсэг бүрийн хэсэг нь \(\frac{1}{6}\) байна.
Өгөгдсөн зурагт бүхэл бүтэн хэдэн хэсэг сүүдэрлэсэн бэ? Нийт 6 хэсгийн 2 хэсэг нь сүүдэртэй тул нийт фракц нь \(\frac{2}{6}\) байна.
Өгөгдсөн зурагт бүхэл бүтэн хэдэн хэсэг сүүдэргүй байна вэ? Нийт 6 хэсгийн 4 хэсэг нь сүүдэргүй тул нийт фракц нь \(\frac{4}{6}\) байна.
Бид мөн бүлгийн хэсгийг төлөөлөхийн тулд бутархайг ашиглаж болно. Нэг анги 12 хүүхэдтэй байхад ангийн багш нь ангийг 2 тэнцүү бүлэгт хуваахыг хүссэн жишээг авч үзье. Бүлэг бүр 6 сурагчтай. 12-ын \(\frac{1}{2}\) нь 6 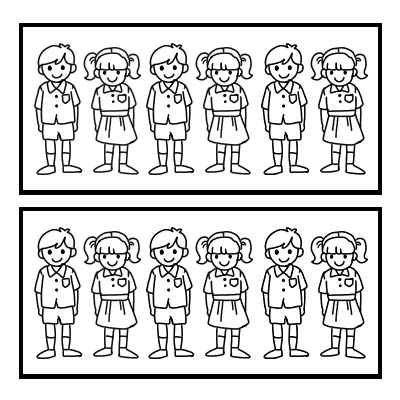
Нэг ангийг 3 тэнцүү бүлэгт хуваасан бол бүлэг тус бүр 4 сурагчтай байна. 12-ын \(\frac{1}{3}\) нь 4.
Доор авч үзсэн фракцын янз бүрийн төрлүүд байдаг.
Зөв бутархай
Зөв бутархай гэдэг нь бүхэл хэсгийг төлөөлөх тоо юм. Тохиромжтой бутархайд хуваагч дахь тоо нь бүхэл хуваагдсан хэсгүүдийн тоог, харин тоологч дахь тоо нь авсан хэсгүүдийн тоог харуулдаг. Тохиромжтой бутархай нь нэгээс бага, хуваагчаас бага тоотой бутархайг хэлнэ.
Жишээлбэл,
\(\frac{2}{5}\) өөрөөр хэлбэл нийт 5 хэсгээс 2 хэсэг
\(\frac{3}{7}\) өөрөөр хэлбэл нийт 7 хэсгээс 3 хэсэг
Буруу бутархай
Тоолуур нь хуваагчаас их байх бутархайг буруу бутархай гэнэ.
Жишээлбэл,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….гэх мэт.
Холимог бутархай
Бүхэл ба хэсгийн хослолыг холимог бутархай гэж нэрлэдэг.
Жишээлбэл,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...гэх мэт.
Бутархай бутархайг холимог бутархай болгон хувиргах
Бутархай бутархайг буруу бутархайн хуваагчаар хуваах замаар холимог бутархай хэлбэрээр илэрхийлж, хуваах ба үлдэгдлийг гаргаж авна. Дараа нь холимог бутархай байх болно
Холимог бутархай = Хэсэг (Үлдэх ∕ Хуваагч)
Холимог бутархайг буруу бутархай болгон хувиргах
Холимог бутархайг дараах байдлаар бичвэл буруу бутархай хэлбэрээр бичиж болно.
[(Бүхэл × хуваагч) + Тоолуур)] ∕ Хугацаа
Бутархай мэт
Ижил хуваагчтай бутархайг бутархайтай адил гэнэ.
Жишээлбэл,
\(\frac{3}{10}\) , \(\frac{4}{10}\) болон \(\frac{7}{10}\) нь бутархайтай адил
Бутархай хэсгээс ялгаатай
Янз бүрийн хуваарьтай бутархайг бутархайтай адилгүй гэнэ.
Жишээлбэл,
\(\frac{3}{7}\) , \(\frac{5}{9}\) болон \(\frac{2}{15}\) нь бутархайтай адилгүй
Эквивалент бутархай
Бүхэлийн ижил хэсгийг төлөөлөх бутархайг тэнцүү бутархай гэнэ.
Жишээлбэл,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Бутархайн хамгийн энгийн хэлбэр
Бутархайг хамгийн энгийн буюу хамгийн бага хэлбэрт хуваагч болон хуваагч нь нэгээс бусад нийтлэг хүчин зүйлгүй гэж нэрлэдэг. Бутархайн хамгийн энгийн хэлбэрийг мөн түүний тоо болон хуваагчийг хамгийн их нийтлэг хүчин зүйлд (HCF) хуваах замаар олж болно. Дээрх жишээн дээр эхний бутархай \(\frac{1}{2}\) хамгийн энгийн хэлбэрээр байна гэж хэлье, учир нь 1 ба 2-т нэгээс бусад нийтлэг хүчин зүйл байхгүй; Хоёрдахь бутархай \(\frac{2}{4}\) нь хамгийн энгийн хэлбэрээр биш, учир нь 2 ба 4 нь 1 ба 2 гэсэн хоёр нийтлэг хүчин зүйлтэй, хэрэв бид 2 ба 4-ийг хамгийн их нийтлэг хүчин зүйлд хуваавал, өөрөөр хэлбэл 2 болно \(\frac{2}{4}\) нь \(\frac{1}{2}\) болох бөгөөд энэ нь одоо бутархайн хамгийн энгийн хэлбэр юм.