အပိုင်းတစ်ခုသည် တစ်ခုလုံး၏ အစိတ်အပိုင်းတစ်ခုဖြစ်သည်။ ပြီးပြည့်စုံသော သို့မဟုတ် အပြည့်အစုံသည် အရာဝတ္ထုတစ်ခုလုံးဖြစ်သည်။ တစ်ခုလုံးသည် အရာဝတ္ထုတစ်စု သို့မဟုတ် အရာဝတ္ထုတစ်ခုတည်း ဖြစ်နိုင်သည်။ အရာတခုလုံးကို အညီအမျှ ပိုင်းခြားပြီး အပိုင်းတစ်ခုစီကို အပိုင်းအစလို့ ခေါ်ပါတယ်။
အောက်ဖော်ပြပါပုံတွင် ပန်းသီးတစ်လုံးလုံးကို နှစ်ခြမ်းခွဲထားသည်။ တစ်ဝက်စီသည် အပိုင်းကိန်းကို \(\frac{1}{2}\) အဖြစ် ကိုယ်စားပြုပြီး 1 သည် ပိုင်းဝေဖြစ်ပြီး 2 သည် ပိုင်းခြေဖြစ်သည်။

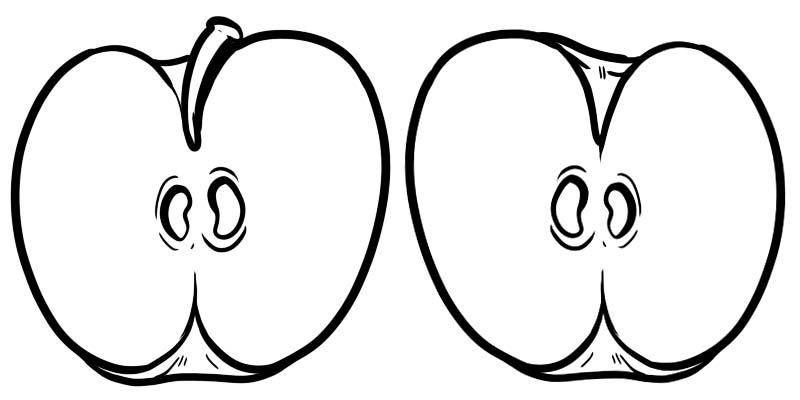
အပိုင်းတစ်ခုအား မျဉ်းတစ်ခုဖြင့် ပိုင်းခြားထားသော ဂဏန်းနှစ်လုံးဖြင့် ဖွဲ့စည်းထားသည်။
စာကြောင်းအောက်တွင် ရေးထားသော နံပါတ်ကို ပိုင်းခြေဟု ခေါ်သည်။ ပိုင်းခြေအားဖြင့် တစ်စုံတစ်ခုအား တူညီသော အစိတ်အပိုင်းများ မည်မျှခွဲထားသည်ကို ပြသသည်။
စာကြောင်းပေါ်တွင် ရေးထားသော နံပါတ်ကို ပိုင်းဝေဟု ခေါ်သည်။ ပိုင်းဝေသည် အစိတ်အပိုင်းတစ်ခုလုံး၏ မည်မျှယူသည်ကို ပြသသည်။
ပိုင်းဝေသည် ပိုင်းခြေထက် ကြီးသည် သို့မဟုတ် သေးနိုင်သည်။
ပိုင်းခြေသည် သုည သို့မဟုတ် တစ်ခုနှင့် မညီမျှပါ။
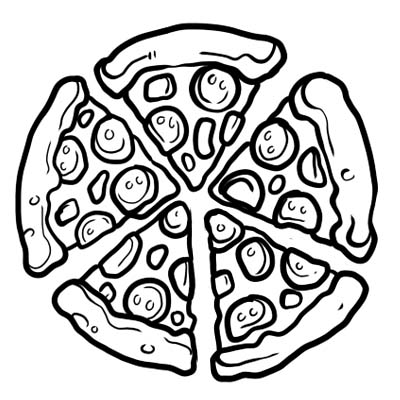
ပီဇာတစ်လုံးကို အညီအမျှ အပိုင်းငါးပိုင်းခွဲထားပါတယ်။ ပီဇာတစ်ချပ်သာ စားပါက ပီဇာတစ်ခုလုံး၏ \(\frac{1}{5}\) ကို စားသည်ဟု ဆိုလိုသည်။ \(\frac{1}{5}\) သည် ဤနေရာတွင် အပိုင်းကိန်းဖြစ်သည်။
ဝက်များနှင့် ရပ်ကွက်များ
Harry နဲ့ Jack က ဗိုက်ဆာတယ်။ ကိတ်မုန့်ဝယ်ကြတယ်။ ကိတ်မုန့်ကို အညီအမျှ နှစ်ပိုင်းခွဲ၍ မျှဝေခဲ့ကြသည်-

ဤတွင်၊ အပိုင်း 1 နှင့် အပိုင်း 2 သည် cupcake ၏အပိုင်းနှစ်ပိုင်းဖြစ်သည်။ အပိုင်း 1 သည် တစ်ဝက်ဖြစ်ပြီး အပိုင်း 2 သည် နောက်ထပ်တစ်ဝက်ဖြစ်သည်။
ရပ်ကွက် (၁/၄) နှင့် လေးပုံသုံးပုံ (၃/၄)၊
Harry၊ Jack၊ Sam နဲ့ Oliver တို့က ချောကလက်တစ်ဘားကို ဝယ်လိုက်တယ်။ အညီအမျှ ၄ ပိုင်း ဖြတ်တယ်။
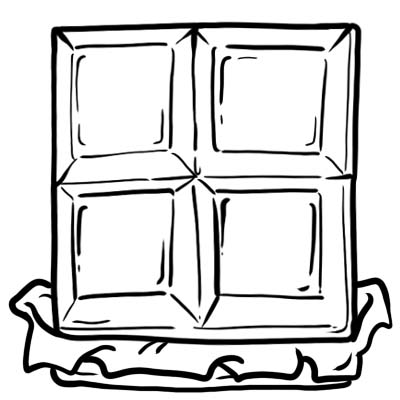
ချောကလက်၏ အစိတ်အပိုင်းတစ်ခုစီ သို့မဟုတ် အတုံးတစ်ခုစီသည် လေးပုံတစ်ပုံ ဆိုလိုသည်မှာ \(\frac{1}{4}\)
ဆိုလိုသည်မှာ၊ ချောကလက်တစ်ခုလုံးကို အညီအမျှ လေးပိုင်းခွဲထားသည်။
Jack က သူ့ရဲ့ချောကလက်တစ်စိတ်တစ်ပိုင်းကို စားခဲ့တယ်ဆိုပါစို့၊ သူ ချောကလက်ရဲ့ လေးပုံတစ်ပုံ ဒါမှမဟုတ် \(\frac{1}{4}\) စားတယ်လို့ ပြောလို့ရပါတယ်။ ချောကလက် ဘယ်လောက်ကျန်သေးလဲ။ အပိုင်း ၃ ပိုင်း ကျန်နေသောကြောင့် \(\frac{3}{4}\) သို့မဟုတ် ချောကလက်၏ လေးပုံသုံးပုံ ကျန်သည်ဟု ပြောနိုင်ပါသည်။
အောက်မှာဖော်ပြထားတဲ့ ပုံလေးကို တစ်ချက်ကြည့်လိုက်ပါ
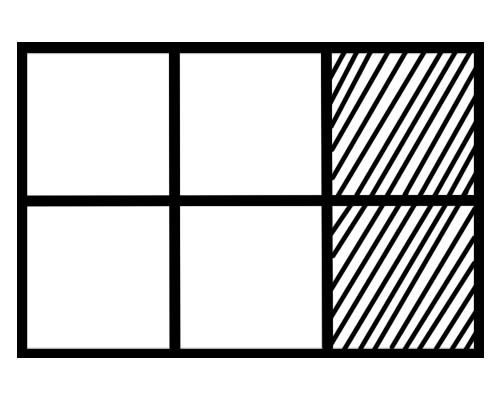
ဤပုံတွင် အစိတ်အပိုင်းတစ်ခုစီ၏ အပိုင်းသည် အဘယ်နည်း။ အညီအမျှ အစိတ်အပိုင်း ခြောက်ခု ရှိသည်၊ ထို့ကြောင့် အပိုင်းတစ်ခုစီ၏ အပိုင်းသည် \(\frac{1}{6}\) ဖြစ်သည်။
ပေးထားသော ပုံတွင် အစိတ်အပိုင်း မည်မျှ အရိပ်ရမည်နည်း။ စုစုပေါင်း 6 ပိုင်း၏ 2 ပိုင်းကို အရိပ်ထိုးထားသောကြောင့် စုစုပေါင်းအပိုင်းကိန်းသည် \(\frac{2}{6}\) ဖြစ်သည်။
ပေးထားသော ပုံတွင် အစိတ်အပိုင်း မည်မျှ အရိပ်မပြသနည်း။ စုစုပေါင်း 6 ပိုင်း၏ 4 ပိုင်းကို အရိပ်မပြထားသောကြောင့် စုစုပေါင်းအပိုင်းသည် \(\frac{4}{6}\) ဖြစ်သည်။
အဖွဲ့တစ်ခု၏ အစိတ်အပိုင်းတစ်ခုကို ကိုယ်စားပြုရန် အပိုင်းကိန်းတစ်ခုကိုလည်း အသုံးပြုနိုင်သည်။ ကျောင်းသား ၁၂ ယောက်ရှိတဲ့ အတန်းတစ်ခုကို ဥပမာတစ်ခုကြည့်ရအောင်၊ အတန်းပိုင်ဆရာက အတန်းကို အတန်းတူအုပ်စု ၂ ခုခွဲစေချင်တယ်။ အုပ်စုတစ်ခုစီတွင် ကျောင်းသား ၆ ဦးရှိမည်ဖြစ်သည်။ 12 ၏ \(\frac{1}{2}\) သည် 6 ဖြစ်သည်။ 
အတန်းတစ်တန်းကို အညီအမျှ အုပ်စု ၃ စု ခွဲမည်ဆိုပါက အုပ်စုတစ်ခုစီတွင် ကျောင်းသား ၄ ဦး ရှိမည်ဖြစ်သည်။ 12 ၏ \(\frac{1}{3}\) သည် 4 ဖြစ်သည်။
အောက်တွင်ဖော်ပြထားသည့်အတိုင်း အပိုင်းခွဲများ ကွဲပြားသောအမျိုးအစားများ ရှိပါသည်။
သင့်လျော်သောအပိုင်းအစများ
သင့်လျော်သောအပိုင်းကိန်းသည် တစ်ခုလုံး၏အစိတ်အပိုင်းတစ်ခုကို ကိုယ်စားပြုသော ဂဏန်းတစ်ခုဖြစ်သည်။ သင့်လျော်သောအပိုင်းကိန်းတစ်ခုတွင်၊ ပိုင်းခြေရှိ နံပါတ်သည် တစ်ခုလုံးကို ပိုင်းခြားထားသည့် အစိတ်အပိုင်းအရေအတွက်ကို ပြသပြီး ပိုင်းဝေရှိ နံပါတ်သည် ထုတ်ယူထားသော အစိတ်အပိုင်းအရေအတွက်ကို ပြသသည်။ သင့်လျော်သောအပိုင်းကိန်းသည် ပိုင်းခြေထက်နည်းသော အပိုင်းကိန်းတစ်ခုထက်နည်းသော အပိုင်းကိန်းတစ်ခုဖြစ်သည်။
ဥပမာအားဖြင့်,
\(\frac{2}{5}\) ဆိုလိုသည်မှာ စုစုပေါင်း 5 ပိုင်းမှ 2 ပိုင်းဖြစ်သည်။
\(\frac{3}{7}\) ဆိုလိုသည်မှာ စုစုပေါင်း 7 ပိုင်းမှ 3 ပိုင်း
မသင့်လျော်သောအပိုင်းအစများ
ပိုင်းဝေသည် ပိုင်းခြေထက် ပိုကြီးသော အပိုင်းကိန်းကို မသင့်လျော်သောအပိုင်းအစဟု ခေါ်သည်။
ဥပမာအားဖြင့်,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….စသည်တို့။
အပိုင်းအစများ ရောနှောထားသည်။
တစ်စိတ်တစ်ပိုင်းနှင့် တစ်ခုလုံးကို ရောစပ်ထားသောအပိုင်းဟု ခေါ်သည်။
ဥပမာအားဖြင့်,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ... စသဖြင့်
မသင့်လျော်သောအပိုင်းကို ရောစပ်ထားသောအပိုင်းအဖြစ်သို့ ပြောင်းလဲခြင်း။
ခွဲကိန်းနှင့် အကြွင်းကို ရယူရန် မသင့်လျော်သောအပိုင်းကိန်း၏ ပိုင်းခြေဖြင့် ပိုင်းခြေဖြင့် ပိုင်းခြားခြင်းဖြင့် ရောစပ်သောအပိုင်းအဖြစ် ဖော်ပြနိုင်သည်။ ထို့နောက် ရောစပ်ထားသောအပိုင်းများ ဖြစ်လိမ့်မည်။
ရောစပ်ထားသောအပိုင်းကိန်း = ပမာဏ (အကြွင်း ∕ ကိန်းဂဏန်း)
ရောစပ်ထားသောအပိုင်းကို မသင့်လျော်သောအပိုင်းအစအဖြစ်သို့ ပြောင်းခြင်း။
ရောစပ်ထားသောအပိုင်းများကို အောက်ပါနည်းလမ်းဖြင့် ရေးသားခြင်းဖြင့် မလျော်ကန်သောအပိုင်းကိန်းပုံစံဖြင့် ရေးသားနိုင်သည်။
[(whole × Denominator) + Numerator)] ∕ ပိုင်းခြေ
အပိုင်းအစများကဲ့သို့
တူညီသော ပိုင်းခြေပါသော အပိုင်းအစများကို အပိုင်းကိန်းများကဲ့သို့ဟု ဆိုပါသည်။
ဥပမာအားဖြင့်,
\(\frac{3}{10}\) ၊ \(\frac{4}{10}\) နှင့် \(\frac{7}{10}\) တို့သည် အပိုင်းအစများ နှင့်တူသည်
အပိုင်းအစများနှင့် မတူပါ။
ကွဲပြားသော ပိုင်းခြေများနှင့် အပိုင်းအစများကို အပိုင်းကိန်းများနှင့် မတူဟု ဆိုပါသည်။
ဥပမာအားဖြင့်,
\(\frac{3}{7}\) ၊ \(\frac{5}{9}\) နှင့် \(\frac{2}{15}\) တို့သည် အပိုင်းကိန်းများနှင့် မတူပါ
ညီမျှသောအပိုင်းအစများ
အစိတ်အပိုင်းတစ်ခုလုံး၏ တူညီသောအစိတ်အပိုင်းများကို ကိုယ်စားပြုသော အပိုင်းအစများကို ညီမျှသောအပိုင်းအစများဟု ဆိုကြသည်။
ဥပမာအားဖြင့်,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
အရိုးရှင်းဆုံးပုံစံက အပိုင်းအစ
၎င်း၏ ပိုင်းဝေနှင့် ပိုင်းခြေတွင် ဘုံအချက်တစ်ချက်မှလွဲ၍ အပိုင်းအခြားမရှိပါက အရိုးရှင်းဆုံးပုံစံ သို့မဟုတ် ၎င်း၏အနိမ့်ဆုံးပုံစံဟု ဆိုပါသည်။ အပိုင်းကိန်း၏ အရိုးရှင်းဆုံးပုံစံကို ၎င်း၏ ပိုင်းဝေနှင့် ပိုင်းခြေကို ၎င်း၏အမြင့်ဆုံးဘုံအချက် (HCF) ဖြင့် ပိုင်းခြားခြင်းဖြင့်လည်း တွေ့ရှိနိုင်သည်။ အထက်ဖော်ပြပါ ဥပမာတွင်၊ ပထမအပိုင်း \(\frac{1}{2}\) သည် 1 နှင့် 2 သည် တစ်ခုမှလွဲ၍ ဘုံအချက်မရှိသဖြင့် ၎င်း၏ အရိုးရှင်းဆုံးပုံစံဖြင့် ဆိုပါစို့။ ဒုတိယအပိုင်း \(\frac{2}{4}\) သည် 2 နှင့် 4 တွင် တူညီသောအချက်နှစ်ချက်ရှိသောကြောင့် 2 နှင့် 4 ကို အမြင့်ဆုံးဘုံအချက်ဖြစ်သည့် 2 ဖြင့် ပိုင်းခြားပါက \(\frac{2}{4}\) \(\frac{1}{2}\) ဖြစ်လာမည်ဖြစ်ပြီး၊ ၎င်းသည် ယခုအခါ အပိုင်းကိန်း၏ အရိုးရှင်းဆုံးပုံစံဖြစ်သည်။