एक अंश सम्पूर्ण को एक भाग हो। एक पूर्ण वा पूर्ण वस्तु एक पूर्ण हो। सम्पूर्ण वस्तुहरूको समूह वा एकल वस्तु हुन सक्छ। जब हामीले कुनै पूरै वस्तुलाई बराबर भागमा विभाजन गर्छौं, तब प्रत्येक भागलाई अंश भनिन्छ।
तलको छविमा, एउटा पूर्ण स्याउ दुई भागमा विभाजन गरिएको छ। प्रत्येक आधा \(\frac{1}{2}\) को रूपमा प्रतिनिधित्व गरिएको एक अंश हो जहाँ 1 अंक हो र 2 भाजक हो।

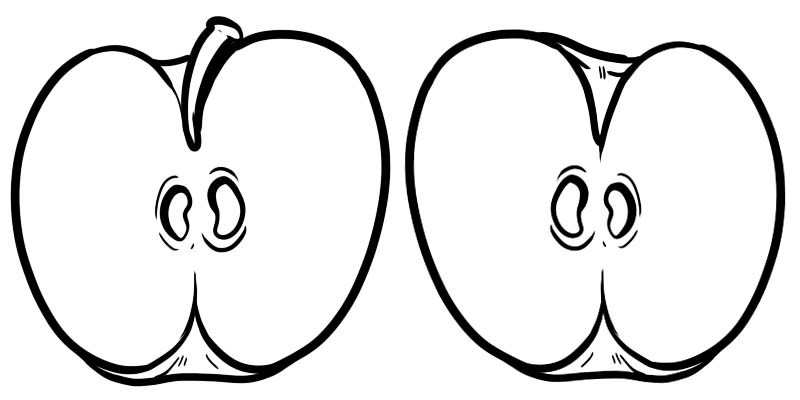
एक अंश दुई संख्याहरू मिलेर बनेको हुन्छ जसलाई रेखाद्वारा विभाजित गरिन्छ।
रेखा मुनि लेखिएको संख्यालाई डिनोमिनेटर भनिन्छ। डिनोमिनेटरले कुनै चीजलाई कति बराबर भागहरूमा विभाजन गरिएको छ भनेर देखाउँछ।
रेखा माथि लेखिएको संख्यालाई अंक भनिन्छ। अंकले सम्पूर्णको कति भागहरू लिइएको छ भनेर देखाउँछ।
अंक भाजक भन्दा ठूलो वा सानो हुन सक्छ।
भाजक शून्य वा एक बराबर छैन।
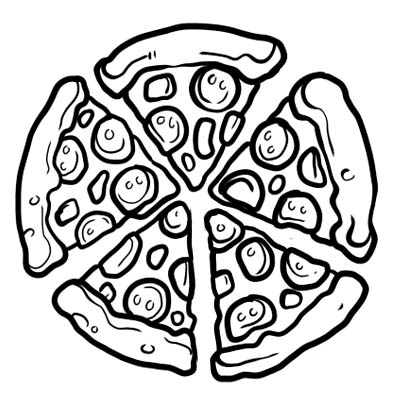
पिज्जालाई पाँच बराबर भागमा विभाजन गरिएको छ। यदि तपाईंले पिज्जाको एक टुक्रा मात्र खानुभयो भने, यसको मतलब तपाईंले सम्पूर्ण पिज्जाको \(\frac{1}{5}\) खानुभयो। \(\frac{1}{5}\) यहाँको अंश हो।
आधा र क्वार्टर
ह्यारी र ज्याक भोकाएका थिए। तिनीहरूले एक कप केक किने। तिनीहरूले कप केकलाई दुई बराबर भागहरूमा विभाजन गरेर साझा गरे:

यहाँ, भाग १ र भाग २ कपकेकका दुई अंश हुन्। भाग १ आधा हो र भाग २ अर्को आधा हो।
क्वार्टर (1/4) र तीन-चौथाई (3/4)
ह्यारी, ज्याक, सैम र ओलिभरले चकलेटको बार किने। तिनीहरूले यसलाई 4 बराबर भागहरूमा काट्छन्।
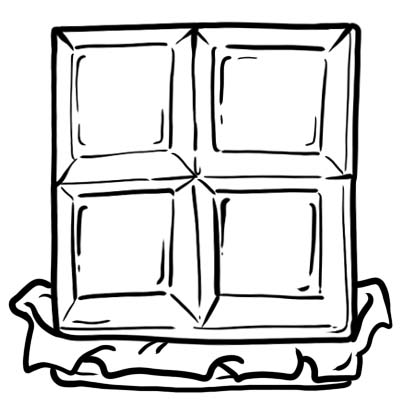
चकलेटको प्रत्येक भाग वा क्यूब एक चौथाई अर्थात् \(\frac{1}{4}\)
यसको मतलब, एक पूरै चकलेट चार बराबर भागहरूमा विभाजित।
मानौं, ज्याकले चकलेटको आफ्नो भाग खायो, हामी भन्न सक्छौं कि उसले चकलेटको एक चौथाई वा \(\frac{1}{4}\) खायो। अब कति चकलेट बाँकी छ? 3 भागहरू बाँकी छन्, त्यसैले हामी भन्न सक्छौं कि \(\frac{3}{4}\) वा तीन चौथाई चकलेट बाँकी छ।
तल दिइएको चित्रमा हेर्नुहोस्,
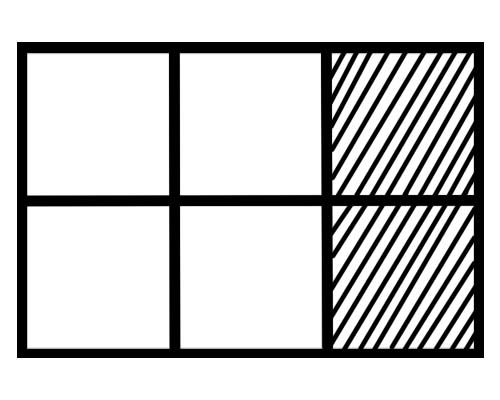
यस चित्रमा प्रत्येक भागको अंश के हो? त्यहाँ छवटा बराबर भागहरू छन्, त्यसैले प्रत्येक भागको अंश \(\frac{1}{6}\) हो।
दिइएको चित्रमा पूरै भागको कति भागलाई छाया गरिएको छ? कुल 6 भागहरू मध्ये 2 भागहरू छायादार छन्, त्यसैले कुल अंश \(\frac{2}{6}\) हो।
दिइएको चित्रमा पूरै भागको कति भाग छायांकन गरिएको छैन? कुल 6 भागहरू मध्ये 4 भागहरू छायादार छैनन्, त्यसैले कुल अंश \(\frac{4}{6}\) हो।
हामी समूह को एक भाग को प्रतिनिधित्व गर्न को लागी एक अंश पनि प्रयोग गर्न सक्छौं। १२ विद्यार्थी भएको कक्षाको उदाहरण लिऔं र कक्षा शिक्षकले कक्षालाई २ समान समूहमा विभाजन गर्न चाहन्छन्। प्रत्येक समूहमा ६ जना विद्यार्थी रहनेछन् । \(\frac{1}{2}\) १२ को ६ हो 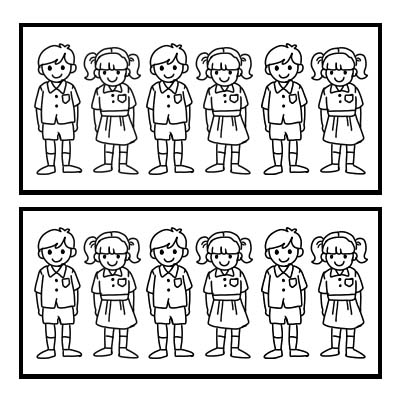
एउटै कक्षालाई ३ समान समूहमा विभाजन गरेमा प्रत्येक समूहमा ४ जना विद्यार्थी हुनेछन्। १२ को \(\frac{1}{3}\) 4 हो।
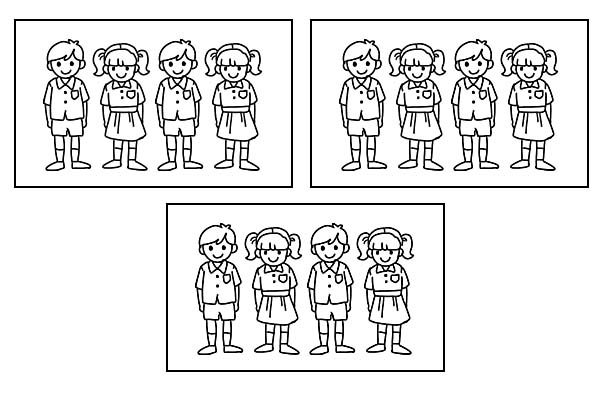
तल चर्चा गरिए अनुसार विभिन्न प्रकारका अंशहरू छन्:
उचित अंशहरू
एक उचित अंश एक संख्या हो जुन सम्पूर्ण को एक भाग को प्रतिनिधित्व गर्दछ। उचित अंशमा, भाजकमा भएको सङ्ख्याले भागहरूको सङ्ख्या देखाउँछ जसमा पूरै भाग गरिएको छ, जबकि अंशमा रहेको सङ्ख्याले लिइएका भागहरूको सङ्ख्या देखाउँछ। उचित अंश भनेको एउटा अंश हो जुन एक भन्दा कम हुन्छ, जसको अंश भाजक भन्दा कम हुन्छ।
उदाहरणका लागि,
\(\frac{2}{5}\) अर्थात् जम्मा ५ भागहरूमध्ये २ भाग
\(\frac{3}{7}\) अर्थात् कुल ७ भागहरूमध्ये ३ भाग
अनुचित अंशहरू
एक अंश जसमा अंश भाजक भन्दा ठूलो छ एक अनुचित अंश भनिन्छ।
उदाहरणका लागि,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) .... आदि।
मिश्रित अंशहरू
पूर्ण र भागको संयोजनलाई मिश्रित अंश भनिन्छ।
उदाहरणका लागि,
३ \(\frac{1}{2}\)
४ \(\frac{3}{4}\) ... आदि।
अनुचित अंशलाई मिश्रित अंशमा रूपान्तरण
भागफल र शेष प्राप्त गर्न अनुचित अंशको भाजकद्वारा अंशलाई भाग गरेर अनुचित अंशलाई मिश्रित अंशको रूपमा व्यक्त गर्न सकिन्छ। त्यसपछि मिश्रित अंश हुनेछ
मिश्रित अंश = भागफल (शेष ∕ भाजक)
मिश्रित अंशलाई अनुचित अंशमा रूपान्तरण
मिश्रित अंशलाई निम्न तरिकाले लेखेर अनुचित अंशको रूपमा लेख्न सकिन्छ:
[(पूर्ण × भाजक) + अंश)] ∕ भाजक
अंशहरू जस्तै
एउटै भाजक भएका भिन्नहरूलाई अंशहरू जस्तै भनिन्छ।
उदाहरणका लागि,
\(\frac{3}{10}\) , \(\frac{4}{10}\) र \(\frac{7}{10}\) अंशहरू जस्तै हुन्
भिन्न भिन्न
भिन्न-भिन्न भाजकहरू भएका अंशहरूलाई भिन्न भिन्न भनिन्छ।
उदाहरणका लागि,
\(\frac{3}{7}\) , \(\frac{5}{9}\) र \(\frac{2}{15}\) भिन्न भिन्न हुन्
बराबर अंशहरू
पूरै भागको एउटै भागलाई प्रतिनिधित्व गर्ने अंशहरूलाई समतुल्य अंश भनिन्छ।
उदाहरणका लागि,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
अंशको सबैभन्दा सरल रूप
अंश र भाजकमा एउटा बाहेक अरू कुनै समान कारक नभएको खण्डमा अंशलाई यसको सरल रूप वा निम्नतम रूप भनिन्छ। अंशको सबैभन्दा सरल रूप यसको अंश र भाजकलाई यसको उच्चतम सामान्य कारक (HCF) द्वारा विभाजित गरेर पनि फेला पार्न सकिन्छ। भन्नुहोस्, माथिको उदाहरणमा, पहिलो अंश \(\frac{1}{2}\) यसको सरल रूपमा छ किनकि 1 र 2 मा एक बाहेक कुनै सामान्य गुणक छैन; दोस्रो अंश \(\frac{2}{4}\) यसको सरल रूपमा छैन किनभने 2 र 4 मा दुईवटा साझा कारकहरू छन् - 1 र 2, यदि हामीले 2 र 4 लाई उच्चतम सामान्य गुणक अर्थात् 2 ले भाग गर्छौं भने \(\frac{2}{4}\) \(\frac{1}{2}\) बन्छ जुन अहिले अंशको सरल रूप हो।