Een breuk is een deel van een geheel. Een compleet of volledig object is een geheel. Een geheel kan een groep objecten of een enkel object zijn. Als we een geheel in gelijke delen verdelen, wordt elk deel een breuk genoemd.
In de onderstaande afbeelding is een volle appel verdeeld in twee helften. Elke helft is een breuk weergegeven als \(\frac{1}{2}\) waarbij 1 de teller is en 2 de noemer.

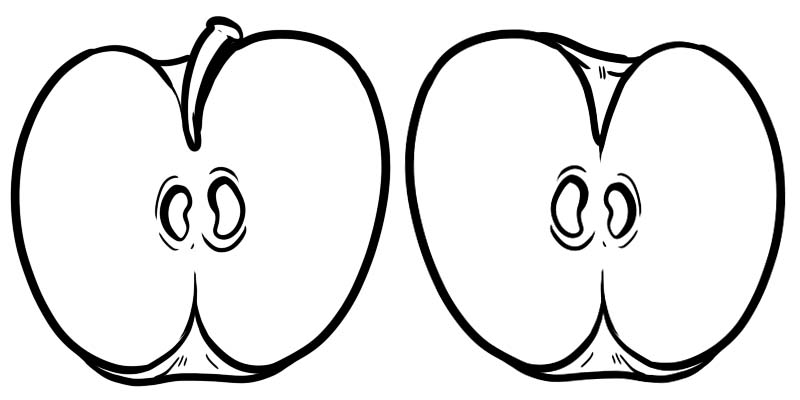
Een breuk bestaat uit twee getallen die gescheiden zijn door een lijn.
Het getal dat onder de lijn staat, staat bekend als de noemer. De noemer geeft aan in hoeveel gelijke delen iets is verdeeld.
Het getal dat boven de lijn wordt geschreven, staat bekend als de teller. De teller geeft aan hoeveel delen van het geheel genomen zijn.
De teller kan groter of kleiner zijn dan de noemer.
De noemer is NIET gelijk aan nul of één.
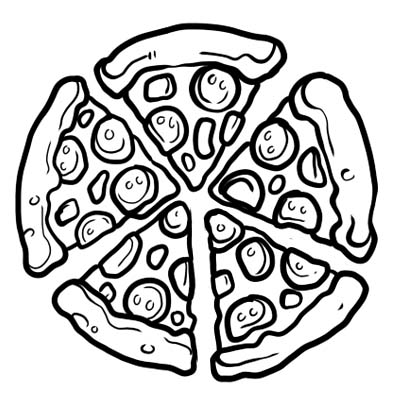
Een pizza is verdeeld in vijf gelijke delen. Als je maar één plak van de pizza eet, betekent dit dat je \(\frac{1}{5}\) van de hele pizza hebt gegeten. \(\frac{1}{5}\) is hier de breuk.
Helften en kwarten
Harry en Jack hadden honger. Ze kochten een koekje. Ze deelden de cupcake door hem in twee gelijke delen te verdelen:

Hier zijn deel 1 en deel 2 twee fracties van de cupcake. Deel 1 is de ene helft en deel 2 is de andere helft.
Kwarten (1/4) en Driekwart (3/4)
Harry, Jack, Sam en Oliver kochten een reep chocola. Ze snijden het in 4 gelijke delen.
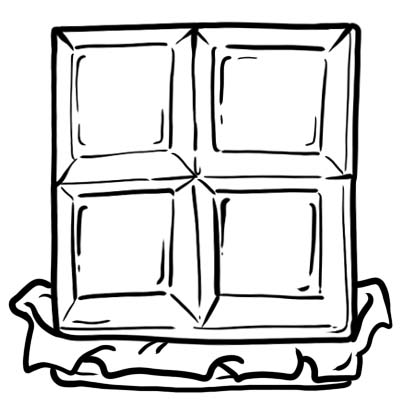
Elk deel of blokje chocolade is een kwart dwz \(\frac{1}{4}\)
Dit betekent dat één hele chocolade in vier gelijke delen wordt verdeeld.
Stel dat Jack zijn deel van de chocolade at, we kunnen zeggen dat hij een vierde of \(\frac{1}{4}\) van de chocolade at. Hoeveel chocolade is er nu nog over? Er zijn nog 3 delen over, dus we kunnen zeggen dat \(\frac{3}{4}\) of driekwart chocolade over is.
Kijk eens naar de onderstaande figuur,
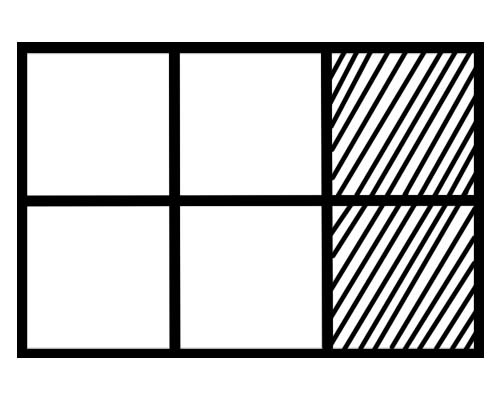
Wat is een fractie van elk deel in deze figuur? Er zijn zes gelijke delen, dus een fractie van elk deel is \(\frac{1}{6}\) .
Hoeveel delen van het geheel zijn gearceerd in de gegeven figuur? 2 delen van de in totaal 6 delen zijn gearceerd, dus de totale breuk is \(\frac{2}{6}\) .
Hoeveel delen van het geheel zijn niet gearceerd in de gegeven figuur? 4 delen van de in totaal 6 delen zijn niet gearceerd, dus de totale breuk is \(\frac{4}{6}\) .
We kunnen ook een breuk gebruiken om een deel van een groep weer te geven. Laten we een voorbeeld nemen van een klas met 12 leerlingen en de klasleraar wil de klas in 2 gelijke groepen verdelen. Elke groep heeft 6 studenten. \(\frac{1}{2}\) van 12 is 6 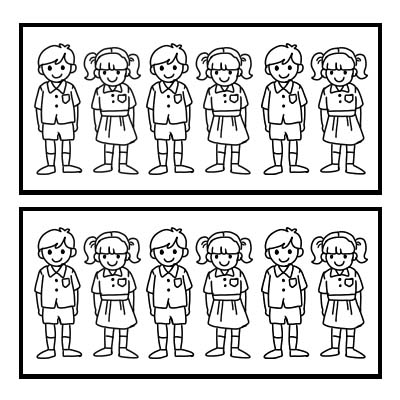
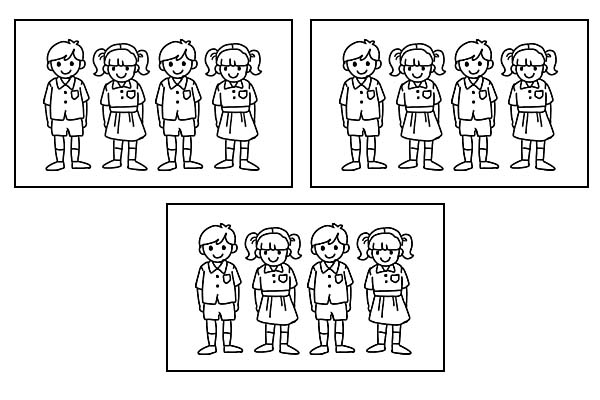
Als dezelfde klas in 3 gelijke groepen wordt verdeeld, heeft elke groep 4 studenten. Omdat \(\frac{1}{3}\) van 12 4 is.
Er zijn verschillende soorten breuken, zoals hieronder besproken:
juiste breuken
Een echte breuk is een getal dat een deel van een geheel voorstelt. In een echte breuk geeft het getal in de noemer het aantal delen weer waarin het geheel is verdeeld, terwijl het getal in de teller het aantal delen aangeeft dat is genomen. Een echte breuk is een breuk die kleiner is dan één, waarbij de teller kleiner is dan de noemer.
Bijvoorbeeld,
\(\frac{2}{5}\) dwz 2 delen van het totaal van 5 delen
\(\frac{3}{7}\) dwz 3 delen van het totaal van 7 delen
Onjuiste breuken
Een breuk waarvan de teller groter is dan de noemer wordt een oneigenlijke breuk genoemd.
Bijvoorbeeld,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….enz.
Gemengde fracties
Een combinatie van een geheel en een deel wordt een gemengde breuk genoemd.
Bijvoorbeeld,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...enz.
Conversie van een onechte breuk in een gemengde breuk
Een onechte breuk kan worden uitgedrukt als een gemengde breuk door de teller te delen door de noemer van de onechte breuk om het quotiënt en de rest te verkrijgen. Dan is de gemengde breuk
Gemengde breuk = Quotiënt (Restant ∕ Deler)
Conversie van een gemengde breuk in een onechte breuk
Een gemengde breuk kan worden geschreven in de vorm van een oneigenlijke breuk door deze op de volgende manier te schrijven:
[(Gehele × noemer) + teller)] ∕ noemer
Zoals breuken
Breuken met dezelfde noemer noemen we gelijke breuken.
Bijvoorbeeld,
\(\frac{3}{10}\) , \(\frac{4}{10}\) en \(\frac{7}{10}\) zijn als breuken
In tegenstelling tot breuken
Breuken met verschillende noemers worden ongelijke breuken genoemd.
Bijvoorbeeld,
\(\frac{3}{7}\) , \(\frac{5}{9}\) en \(\frac{2}{15}\) zijn ongelijke breuken
Gelijkwaardige breuken
Breuken die hetzelfde deel van een geheel vertegenwoordigen, worden equivalente breuken genoemd.
Bijvoorbeeld,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
De eenvoudigste vorm van een breuk
Er wordt gezegd dat een breuk in zijn eenvoudigste of laagste vorm is als de teller en noemer geen gemeenschappelijke factor hebben behalve één. De eenvoudigste vorm van een breuk kan ook worden gevonden door de teller en noemer te delen door de hoogste gemene deler (HCF). Stel dat in het bovenstaande voorbeeld de eerste breuk \(\frac{1}{2}\) in zijn eenvoudigste vorm is, aangezien 1 en 2 geen gemeenschappelijke factor hebben behalve één; de tweede breuk \(\frac{2}{4}\) is niet in zijn eenvoudigste vorm omdat 2 en 4 twee gemeenschappelijke factoren hebben – 1 en 2, als we 2 en 4 delen door de hoogste gemene deler, namelijk 2, dan \(\frac{2}{4}\) wordt \(\frac{1}{2}\) wat nu de eenvoudigste vorm van de breuk is.