Ułamek to część całości. Kompletny lub pełny przedmiot jest całością. Całość może być grupą obiektów lub pojedynczym obiektem. Kiedy dzielimy całość na równe części, wówczas każdą część nazywamy ułamkiem.
Na poniższym obrazku jedno pełne jabłko jest podzielone na dwie połówki. Każda połowa to ułamek reprezentowany jako \(\frac{1}{2}\) gdzie 1 to licznik, a 2 to mianownik.

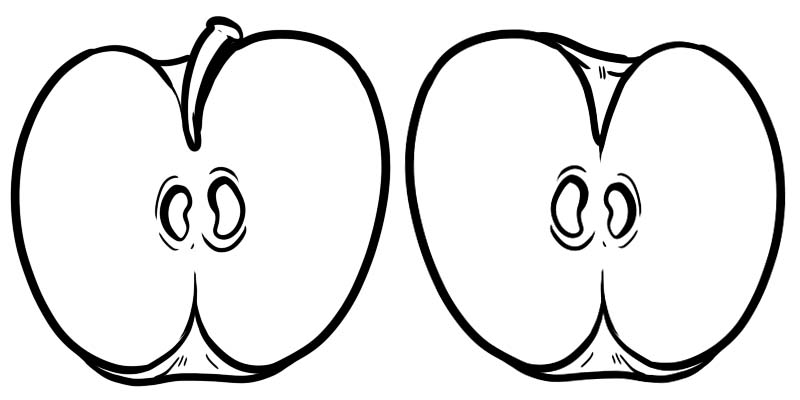
Ułamek składa się z dwóch liczb podzielonych linią.
Liczba zapisana pod kreską nazywana jest mianownikiem. Mianownik pokazuje, na ile równych części coś zostało podzielone.
Liczba zapisana nad linią nazywana jest licznikiem. Licznik pokazuje, ile części całości zostało wziętych.
Licznik może być większy lub mniejszy od mianownika.
Mianownik NIE jest równy zero ani jeden.
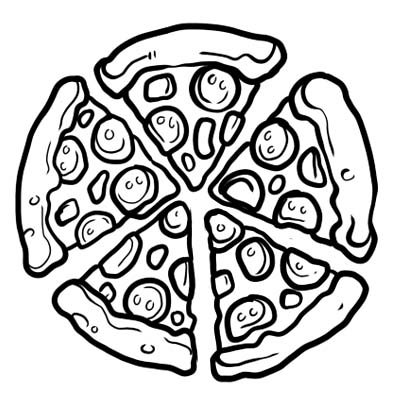
Pizza jest podzielona na pięć równych części. Jeśli zjesz tylko jeden kawałek pizzy, oznacza to, że zjadłeś \(\frac{1}{5}\) całą pizzę. \(\frac{1}{5}\) to tutaj ułamek.
Połówki i ćwiartki
Harry i Jack byli głodni. Kupili ciastko. Podzielili się babeczką, dzieląc ją na dwie równe części:

Tutaj część 1 i część 2 to dwie frakcje babeczki. Część 1 to połowa, a część 2 to druga połowa.
Ćwiartki (1/4) i trzy czwarte (3/4)
Harry, Jack, Sam i Oliver kupili tabliczkę czekolady. Kroją go na 4 równe części.
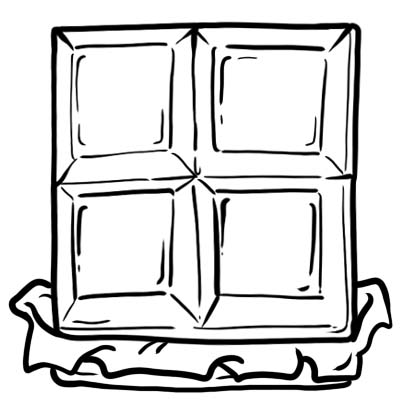
Każda część lub kostka czekolady to jedna czwarta, tj. \(\frac{1}{4}\)
Oznacza to, że jedna cała czekolada podzielona na cztery równe części.
Załóżmy, że Jack zjadł swoją część czekolady, możemy powiedzieć, że zjadł jedną czwartą lub \(\frac{1}{4}\) czekolady. Ile czekolady zostało teraz? Zostały 3 części, więc możemy powiedzieć, że zostało \(\frac{3}{4}\) lub trzy czwarte czekolady.
Przyjrzyj się poniższemu rysunkowi,
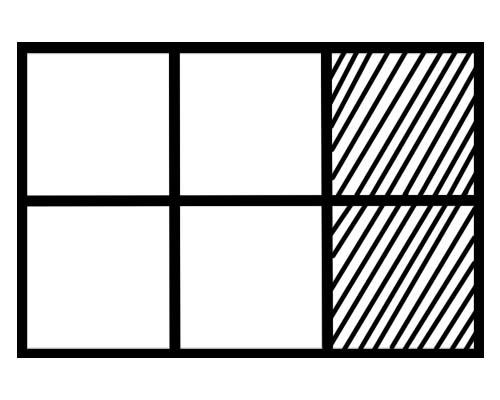
Ile wynosi ułamek każdej części na tej figurze? Jest sześć równych części, więc ułamek każdej części to \(\frac{1}{6}\) .
Ile części całości jest zacieniowanych na podanej figurze? 2 części z 6 części są zacieniowane, więc całkowity ułamek to \(\frac{2}{6}\) .
Ile części całości nie jest zacieniowanych na podanej figurze? 4 części z 6 części nie są zacienione, więc całkowity ułamek to \(\frac{4}{6}\) .
Możemy również użyć ułamka do przedstawienia części grupy. Weźmy przykład klasy, w której jest 12 uczniów i wychowawca klasy chce podzielić klasę na 2 równe grupy. W każdej grupie będzie 6 uczniów. \(\frac{1}{2}\) z 12 to 6 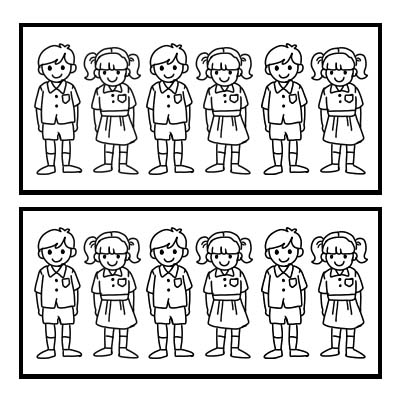
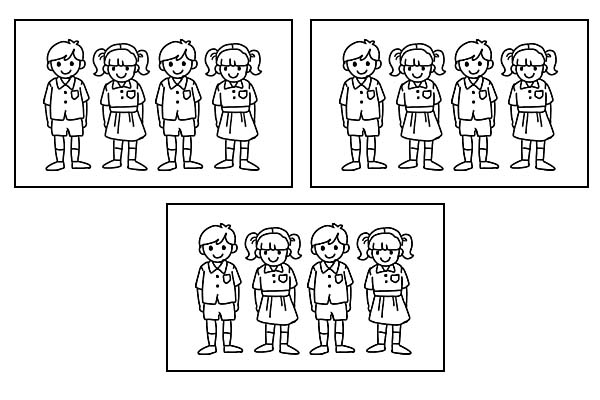
Jeśli ta sama klasa zostanie podzielona na 3 równe grupy, każda grupa będzie liczyć 4 uczniów. Ponieważ \(\frac{1}{3}\) liczby 12 równa się 4.
Istnieją różne rodzaje ułamków, jak omówiono poniżej:
Ułamki właściwe
Ułamek właściwy to liczba reprezentująca część całości. W ułamku właściwym liczba w mianowniku oznacza liczbę części, na które dzieli się całość, natomiast liczba w liczniku wskazuje liczbę części, które zostały pobrane. Ułamek właściwy to ułamek mniejszy niż jeden, w którym licznik jest mniejszy od mianownika.
Na przykład,
\(\frac{2}{5}\) czyli 2 części z 5 części
\(\frac{3}{7}\) czyli 3 części z 7 części
Ułamki niewłaściwe
Ułamek, w którym licznik jest większy od mianownika, nazywamy ułamkiem niewłaściwym.
Na przykład,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….etc.
Frakcje mieszane
Połączenie całości i części nazywamy ułamkiem mieszanym.
Na przykład,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...itp.
Zamiana ułamka niewłaściwego na ułamek mieszany
Ułamek niewłaściwy można wyrazić jako ułamek mieszany, dzieląc licznik przez mianownik ułamka niewłaściwego, aby otrzymać iloraz i resztę. Wtedy frakcja mieszana będzie
Ułamek mieszany = iloraz (reszta ∕ dzielnik)
Zamiana ułamka mieszanego na ułamek niewłaściwy
Ułamek mieszany można zapisać w postaci ułamka niewłaściwego, zapisując go w następujący sposób:
[(całość × mianownik) + licznik)] ∕ mianownik
Jak ułamki
Mówi się, że ułamki o tym samym mianowniku są jak ułamki.
Na przykład,
\(\frac{3}{10}\) , \(\frac{4}{10}\) i \(\frac{7}{10}\) są jak ułamki zwykłe
W przeciwieństwie do ułamków
Mówi się, że ułamki o różnych mianownikach różnią się od ułamków zwykłych.
Na przykład,
\(\frac{3}{7}\) , \(\frac{5}{9}\) i \(\frac{2}{15}\) różnią się od ułamków zwykłych
Równoważne ułamki
O ułamkach, które reprezentują tę samą część całości, mówi się, że są ułamkami równoważnymi.
Na przykład,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Najprostsza postać ułamka
Mówimy, że ułamek ma najprostszą lub najniższą postać, jeśli jego licznik i mianownik nie mają wspólnego dzielnika poza jednym. Najprostszą postać ułamka można również znaleźć, dzieląc jego licznik i mianownik przez jego najwyższy wspólny czynnik (HCF). Załóżmy, że w powyższym przykładzie pierwszy ułamek \(\frac{1}{2}\) jest w najprostszej postaci, ponieważ 1 i 2 nie mają wspólnego dzielnika poza jednym; drugi ułamek \(\frac{2}{4}\) nie jest w najprostszej postaci ponieważ 2 i 4 mają dwa wspólne dzielniki – 1 i 2, jeśli podzielimy 2 i 4 przez najwyższy wspólny dzielnik czyli 2 to \(\frac{2}{4}\) zmieni się w \(\frac{1}{2}\) który jest teraz najprostszą postacią ułamka.