Uma fração é uma parte de um todo. Um objeto completo ou completo é um todo. Um todo pode ser um grupo de objetos ou um único objeto. Quando dividimos uma coisa inteira em partes iguais, cada parte é chamada de fração.
Na imagem abaixo, uma maçã cheia é dividida em duas metades. Cada metade é uma fração representada como \(\frac{1}{2}\) onde 1 é o numerador e 2 é o denominador.

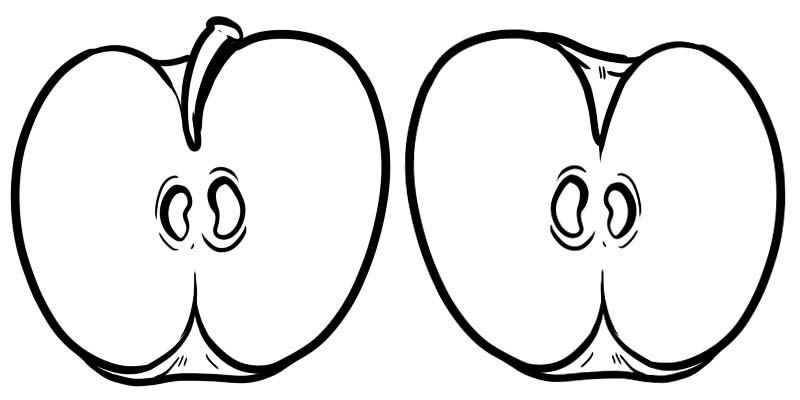
Uma fração é composta por dois números que são divididos por uma linha.
O número que está escrito abaixo da linha é conhecido como denominador. O denominador mostra em quantas partes iguais algo foi dividido.
O número que está escrito acima da linha é conhecido como numerador. O numerador mostra quantas partes do todo são tomadas.
O numerador pode ser maior ou menor que o denominador.
O denominador NÃO é igual a zero ou um.
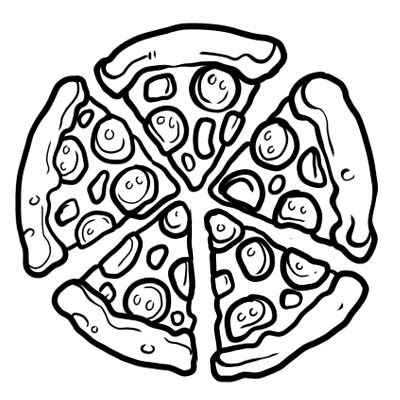
Uma pizza é dividida em cinco partes iguais. Se você comer apenas uma fatia da pizza, significa que você comeu \(\frac{1}{5}\) da pizza inteira. \(\frac{1}{5}\) é a fração aqui.
Metades e quartos
Harry e Jack estavam com fome. Eles compraram um cupcake. Eles dividiram o cupcake dividindo-o em duas partes iguais:

Aqui, a Parte 1 e a Parte 2 são duas frações do cupcake. A parte 1 é uma metade e a parte 2 é outra metade.
Quartos (1/4) e Três Quartos (3/4)
Harry, Jack, Sam e Oliver compraram uma barra de chocolate. Eles cortaram em 4 partes iguais.
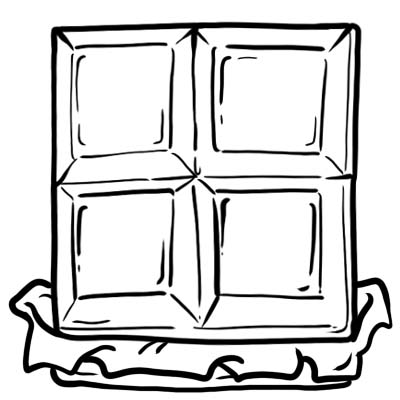
Cada parte ou cubo de chocolate é um quarto, ou seja, \(\frac{1}{4}\)
Ou seja, um chocolate inteiro dividido em quatro partes iguais.
Suponha que Jack comeu sua parte de chocolate, podemos dizer que ele comeu um quarto ou \(\frac{1}{4}\) do chocolate. Quanto chocolate resta agora? Restam 3 partes, então podemos dizer que resta \(\frac{3}{4}\) ou três quartos de chocolate.
Observe a figura abaixo,
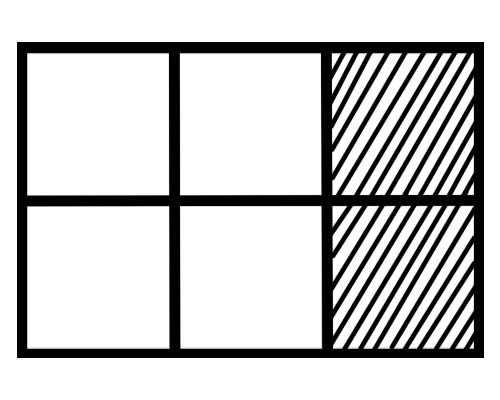
Qual é uma fração de cada parte nesta figura? Existem seis partes iguais, então uma fração de cada parte é \(\frac{1}{6}\) .
Quantas partes do todo estão sombreadas na figura dada? 2 partes do total de 6 partes estão sombreadas, então a fração total é \(\frac{2}{6}\) .
Quantas partes do todo não estão sombreadas na figura dada? 4 partes do total de 6 partes não estão sombreadas, então a fração total é \(\frac{4}{6}\) .
Também podemos usar uma fração para representar uma parte de um grupo. Vamos dar um exemplo de uma turma com 12 alunos e o professor da turma quer dividir a turma em 2 grupos iguais. Cada grupo terá 6 alunos. \(\frac{1}{2}\) de 12 é 6 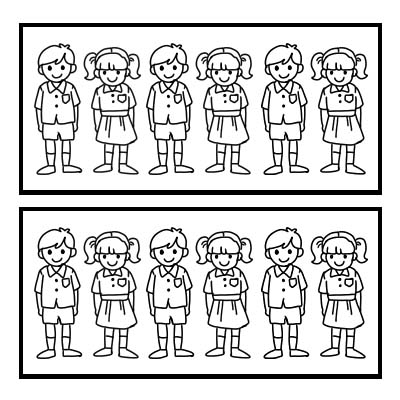
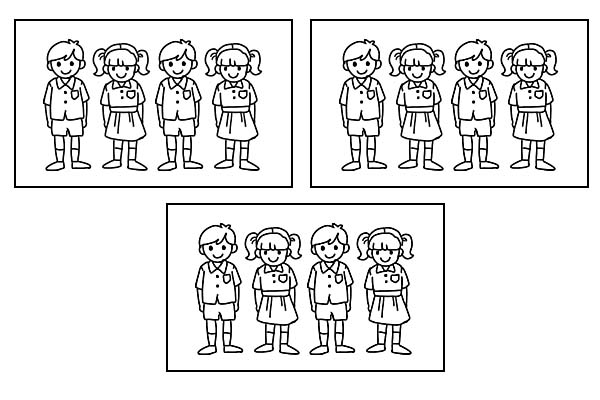
Se a mesma turma for dividida em 3 grupos iguais, cada grupo terá 4 alunos. Como \(\frac{1}{3}\) de 12 é 4.
Existem diferentes tipos de frações, conforme discutido abaixo:
Frações próprias
Uma fração própria é um número que representa uma parte de um todo. Em uma fração própria, o número no denominador mostra o número de partes em que o todo é dividido, enquanto o número no numerador mostra o número de partes que foram tomadas. Uma fração própria é uma fração que é menor que um, com o numerador menor que o denominador.
Por exemplo,
\(\frac{2}{5}\) ou seja, 2 partes do total de 5 partes
\(\frac{3}{7}\) ou seja, 3 partes do total de 7 partes
Frações impróprias
Uma fração em que o numerador é maior que o denominador é chamada de fração imprópria.
Por exemplo,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….etc.
Frações mistas
Uma combinação de um todo e uma parte é chamada de fração mista.
Por exemplo,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...etc.
Conversão de uma fração imprópria em uma fração mista
Uma fração imprópria pode ser expressa como uma fração mista dividindo o numerador pelo denominador da fração imprópria para obter o quociente e o resto. Então a fração mista será
Fração Mista = Quociente (Remanescente ∕ Divisor)
Conversão de uma fração mista em uma fração imprópria
Uma fração mista pode ser escrita na forma de uma fração imprópria escrevendo-a da seguinte maneira:
[(Inteiro × Denominador) + Numerador)] ∕ Denominador
Como frações
Frações com o mesmo denominador são ditas como frações.
Por exemplo,
\(\frac{3}{10}\) , \(\frac{4}{10}\) e \(\frac{7}{10}\) são como frações
Ao contrário das frações
Frações com denominadores diferentes são ditas frações diferentes.
Por exemplo,
\(\frac{3}{7}\) , \(\frac{5}{9}\) e \(\frac{2}{15}\) são diferentes de frações
Frações equivalentes
Frações que representam a mesma parte de um todo são chamadas frações equivalentes.
Por exemplo,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
A forma mais simples de uma fração
Diz-se que uma fração está em sua forma mais simples ou em sua forma mais baixa se seu numerador e denominador não tiverem fator comum, exceto um. A forma mais simples de uma fração também pode ser encontrada dividindo seu numerador e denominador pelo maior fator comum (HCF). Digamos que, no exemplo acima, a primeira fração \(\frac{1}{2}\) esteja em sua forma mais simples, pois 1 e 2 não têm fator comum exceto um; a segunda fração \(\frac{2}{4}\) não está em sua forma mais simples porque 2 e 4 têm dois fatores comuns – 1 e 2, se dividirmos 2 e 4 pelo maior fator comum, ou seja, 2, então \(\frac{2}{4}\) se tornará \(\frac{1}{2}\) que agora é a forma mais simples da fração.