Дробь – это часть целого. Полный или полный объект представляет собой целое. Целое может быть группой объектов или одним объектом. Когда мы делим целое на равные части, то каждая часть называется дробью.
На изображении ниже одно полное яблоко разделено на две половинки. Каждая половина представляет собой дробь, представленную в виде \(\frac{1}{2}\) , где 1 — числитель, а 2 — знаменатель.

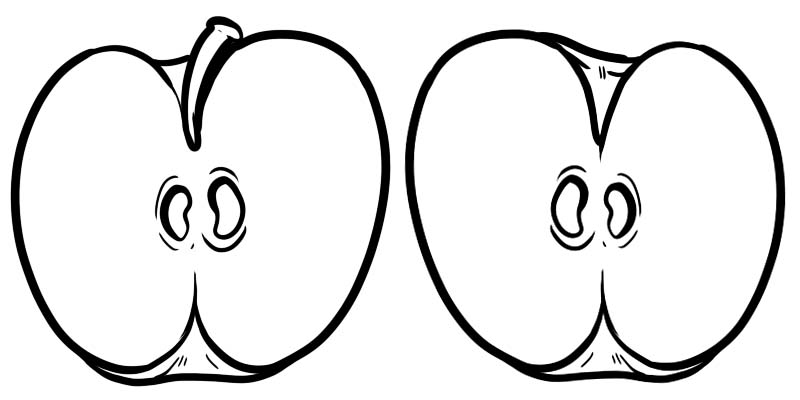
Дробь состоит из двух чисел, которые разделены чертой.
Число, написанное под чертой, называется знаменателем. Знаменатель показывает, на сколько равных частей что-то было разделено.
Число, написанное над чертой, называется числителем. Числитель показывает, сколько частей целого взято.
Числитель может быть больше или меньше знаменателя.
Знаменатель НЕ равен нулю или единице.
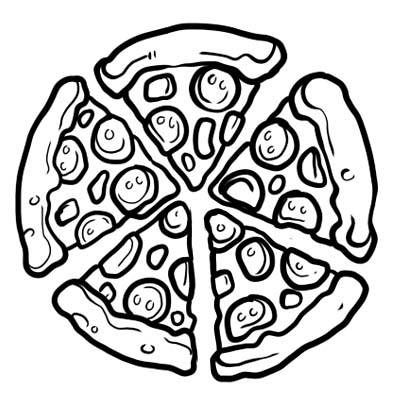
Пицца разделена на пять равных частей. Если вы съели только один кусок пиццы, это означает, что вы съели \(\frac{1}{5}\) всей пиццы. \(\frac{1}{5}\) здесь дробь.
Половинки и четвертинки
Гарри и Джек были голодны. Они купили кекс. Они поделили кекс, разделив его на две равные части:

Здесь Часть 1 и Часть 2 — это две части кекса. Часть 1 - это половина, а часть 2 - другая половина.
Четверти (1/4) и три четверти (3/4)
Гарри, Джек, Сэм и Оливер купили плитку шоколада. Они разрезали его на 4 равные части.
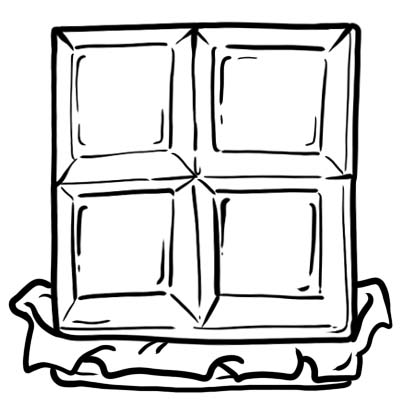
Каждая часть или кубик шоколада составляет одну четверть, т.е. \(\frac{1}{4}\)
Это означает, что одна целая шоколадка разделена на четыре равные части.
Предположим, Джек съел свою часть шоколада, можно сказать, что он съел одну четвертую или \(\frac{1}{4}\) шоколада. Сколько шоколада осталось? Осталось 3 части, поэтому можно сказать, что осталось \(\frac{3}{4}\) или три четверти шоколада.
Взгляните на рисунок, приведенный ниже,
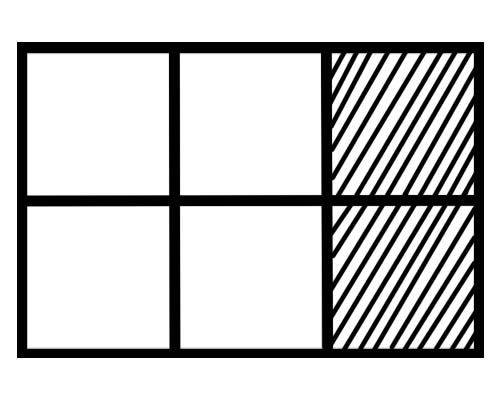
Какова доля каждой части этой фигуры? Есть шесть равных частей, поэтому доля каждой части равна \(\frac{1}{6}\) .
Сколько частей целого заштриховано на данном рисунке? 2 части из 6 частей заштрихованы, поэтому общая дробь равна \(\frac{2}{6}\) .
Сколько частей целого не заштриховано на данном рисунке? 4 части из 6 частей не заштрихованы, поэтому общая дробь равна \(\frac{4}{6}\) .
Мы также можем использовать дробь для представления части группы. Давайте возьмем пример класса с 12 учениками, и классный руководитель хочет разделить класс на 2 равные группы. В каждой группе будет по 6 учеников. \(\frac{1}{2}\) из 12 равно 6 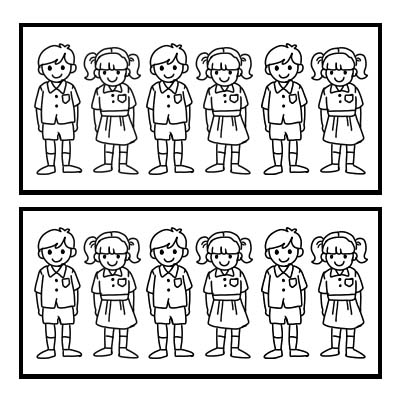
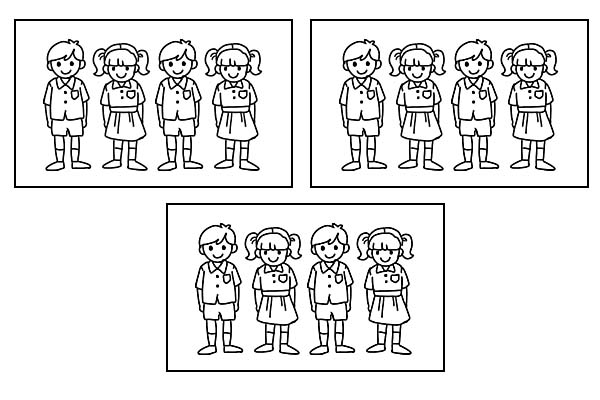
Если один и тот же класс разделить на 3 равные группы, в каждой группе будет по 4 ученика. Поскольку \(\frac{1}{3}\) от 12 равно 4.
Существуют различные типы фракций, как описано ниже:
Правильные дроби
Правильная дробь – это число, представляющее часть целого. В правильной дроби число в знаменателе показывает количество частей, на которые делится целое, а число в числителе показывает количество частей, которые были взяты. Правильная дробь – это дробь меньше единицы, у которой числитель меньше знаменателя.
Например,
\(\frac{2}{5}\) т.е. 2 части из 5 частей
\(\frac{3}{7}\) т.е. 3 части из 7 частей
Неправильные дроби
Дробь, у которой числитель больше знаменателя, называется неправильной дробью.
Например,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….и т.д.
Смешанные фракции
Сочетание целого и части называется смешанной дробью.
Например,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...и т.д.
Преобразование неправильной дроби в смешанную дробь
Неправильную дробь можно представить в виде смешанной дроби, разделив числитель на знаменатель неправильной дроби, чтобы получить частное и остаток. Тогда смешанная дробь будет
Смешанная дробь = частное (остаток ∕ делитель)
Преобразование смешанной дроби в неправильную дробь
Смешанную дробь можно записать в виде неправильной дроби, записав ее следующим образом:
[(целое × знаменатель) + числитель)] ∕ знаменатель
Как дроби
Дроби с одинаковыми знаменателями называются подобными дробям.
Например,
\(\frac{3}{10}\) , \(\frac{4}{10}\) и \(\frac{7}{10}\) похожи на дроби
В отличие от дробей
Дроби с разными знаменателями называются непохожими дробями.
Например,
\(\frac{3}{7}\) , \(\frac{5}{9}\) и \(\frac{2}{15}\) не похожи на дроби
Эквивалентные дроби
Дроби, представляющие одну и ту же часть целого, называются эквивалентными дробями.
Например,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Простейшая форма дроби
Говорят, что дробь имеет простейшую или наименьшую форму, если ее числитель и знаменатель не имеют общего делителя, кроме одного. Простейшую форму дроби также можно найти, разделив ее числитель и знаменатель на ее наибольший общий делитель (HCF). Скажем, в приведенном выше примере первая дробь \(\frac{1}{2}\) имеет простейшую форму, поскольку 1 и 2 не имеют общего делителя, кроме одного; вторая дробь \(\frac{2}{4}\) не имеет простейшей формы, потому что 2 и 4 имеют два общих делителя - 1 и 2, если мы разделим 2 и 4 на наибольший общий делитель, т.е. 2, то \(\frac{2}{4}\) станет \(\frac{1}{2}\) , что теперь является простейшей формой дроби.