Një thyesë është pjesë e një tërësie. Një objekt i plotë ose i plotë është një tërësi. Një e tërë mund të jetë një grup objektesh ose një objekt i vetëm. Kur një send të tërë e ndajmë në pjesë të barabarta, atëherë secila pjesë quhet thyesë.
Në imazhin e mëposhtëm, një mollë e plotë është e ndarë në dy gjysma. Çdo gjysmë është një thyesë e paraqitur si \(\frac{1}{2}\) ku 1 është numëruesi dhe 2 është emëruesi.

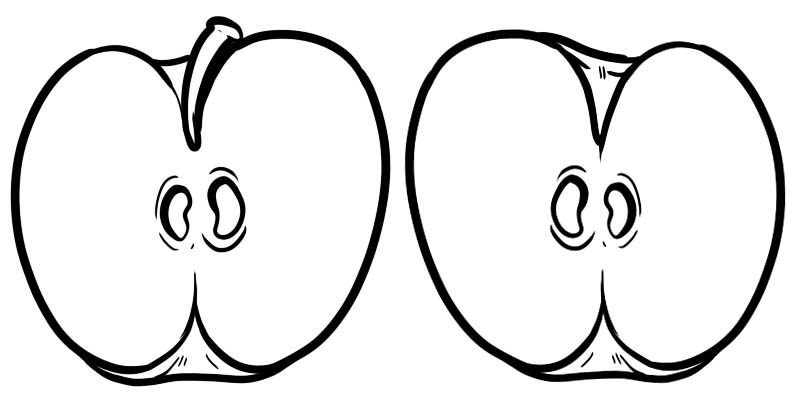
Një thyesë përbëhet nga dy numra të cilët ndahen me një vijë.
Numri që shkruhet poshtë vijës njihet si emërues. Emëruesi tregon në sa pjesë të barabarta është ndarë diçka.
Numri që shkruhet sipër rreshtit njihet si numërues. Numëruesi tregon se sa pjesë të së tërës janë marrë.
Numëruesi mund të jetë më i madh ose më i vogël se emëruesi.
Emëruesi NUK është i barabartë me zero ose një.
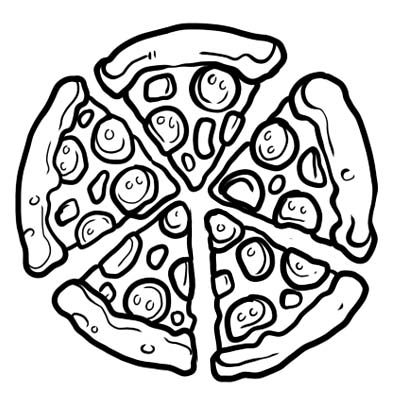
Pica ndahet në pesë pjesë të barabarta. Nëse hani vetëm një fetë nga pica, do të thotë se keni ngrënë \(\frac{1}{5}\) nga e gjithë pica. \(\frac{1}{5}\) është thyesa këtu.
Gjysmat dhe të katërtat
Harry dhe Jack ishin të uritur. Ata blenë një kek i vockël. Ata e ndanë kekun duke e ndarë në dy pjesë të barabarta:

Këtu, Pjesa 1 dhe Pjesa 2 janë dy fraksione të kekut të kekut. Pjesa 1 është një gjysmë dhe Pjesa 2 është një gjysmë tjetër.
Çereku (1/4) dhe treçereku (3/4)
Harry, Jack, Sam dhe Oliver blenë një copë çokollatë. E presin në 4 pjesë të barabarta.
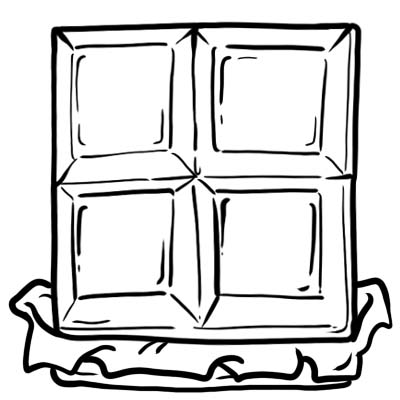
Çdo pjesë ose kub çokollatë është një e katërta dmth \(\frac{1}{4}\)
Kjo do të thotë, një çokollatë e tërë e ndarë në katër pjesë të barabarta.
Supozoni se Jack hëngri pjesën e tij të çokollatës, mund të themi se ai hëngri një të katërtën ose \(\frac{1}{4}\) të çokollatës. Sa çokollatë ka mbetur tani? Kanë mbetur 3 pjesë, ndaj mund të themi se ka mbetur \(\frac{3}{4}\) ose tre të katërtat e çokollatës.
Hidhini një sy figurës së dhënë më poshtë,
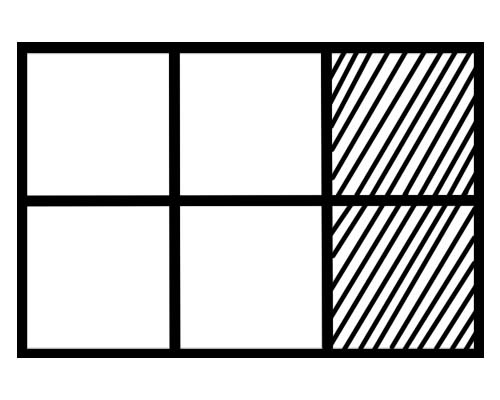
Sa është një pjesë e secilës pjesë në këtë figurë? Janë gjashtë pjesë të barabarta, kështu që një pjesë e secilës pjesë është \(\frac{1}{6}\) .
Sa pjesë të tërësisë janë të hijezuara në figurën e dhënë? 2 pjesë nga 6 pjesët totale janë të hijezuara, kështu që fraksioni total është \(\frac{2}{6}\) .
Sa pjesë të së tërës nuk janë të hijezuara në figurën e dhënë? 4 pjesë nga 6 pjesët e përgjithshme nuk janë të hijezuara, kështu që thyesa totale është \(\frac{4}{6}\) .
Mund të përdorim edhe një thyesë për të përfaqësuar një pjesë të një grupi. Le të marrim një shembull të një klase me 12 nxënës dhe mësuesi i klasës dëshiron ta ndajë klasën në 2 grupe të barabarta. Secili grup do të ketë 6 nxënës. \(\frac{1}{2}\) nga 12 është 6 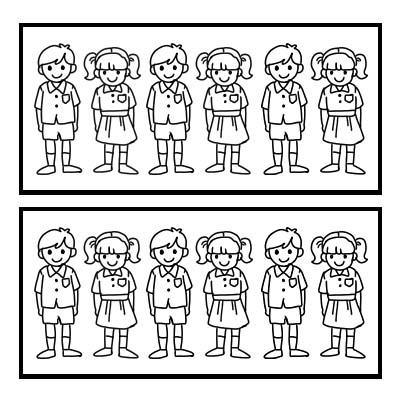
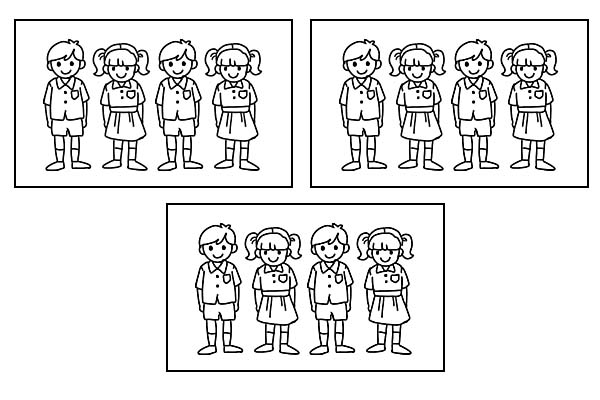
Nëse e njëjta klasë ndahet në 3 grupe të barabarta, secili grup do të ketë 4 nxënës. Pasi \(\frac{1}{3}\) nga 12 është 4.
Ekzistojnë lloje të ndryshme të fraksioneve siç diskutohen më poshtë:
Thyesat e duhura
Një thyesë e duhur është një numër që përfaqëson një pjesë të një tërësie. Në një thyesë të duhur, numri në emërues tregon numrin e pjesëve në të cilat është ndarë e tëra, ndërsa numri në numërues tregon numrin e pjesëve që janë marrë. Një thyesë e duhur është një thyesë që është më e vogël se një, me numëruesin më të vogël se emëruesi.
Për shembull,
\(\frac{2}{5}\) dmth 2 pjesë nga gjithsej 5 pjesë
\(\frac{3}{7}\) dmth 3 pjesë nga gjithsej 7 pjesë
Thyesat e gabuara
Një thyesë në të cilën numëruesi është më i madh se emëruesi quhet thyesë e papërshtatshme.
Për shembull,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) … etj.
Fraksionet e përziera
Kombinimi i një tërësie dhe një pjese quhet thyesë e përzier.
Për shembull,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...etj.
Shndërrimi i një thyese të papërshtatshme në një fraksion të përzier
Një thyesë e papërshtatshme mund të shprehet si një thyesë e përzier duke pjesëtuar numëruesin me emëruesin e thyesës së papërshtatshme për të marrë herësin dhe pjesën e mbetur. Atëherë fraksioni i përzier do të jetë
Thyesë e përzier = Koeficient (pjesëtuesi i mbetur ∕)
Shndërrimi i një thyese të përzier në një fraksion të papërshtatshëm
Një thyesë e përzier mund të shkruhet në formën e një thyese jo të duhur duke e shkruar atë në mënyrën e mëposhtme:
[(E gjithë × Emëruesi) + Numëruesi)] ∕ Emëruesi
Ashtu si thyesat
Thyesat me emërues të njëjtë thuhet se janë si thyesat.
Për shembull,
\(\frac{3}{10}\) , \(\frac{4}{10}\) dhe \(\frac{7}{10}\) janë si thyesa
Ndryshe nga thyesat
Thyesat me emërues të ndryshëm thuhet se janë ndryshe nga thyesat.
Për shembull,
\(\frac{3}{7}\) , \(\frac{5}{9}\) dhe \(\frac{2}{15}\) nuk ngjajnë me thyesat
Thyesat ekuivalente
Thyesat që përfaqësojnë të njëjtën pjesë të një tërësie quhen thyesa ekuivalente.
Për shembull,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Forma më e thjeshtë e një thyese
Një thyesë quhet në formën e saj më të thjeshtë ose në formën e saj më të ulët nëse numëruesi dhe emëruesi i saj nuk kanë faktor të përbashkët përveç njërit. Forma më e thjeshtë e një thyese mund të gjendet gjithashtu duke pjesëtuar numëruesin dhe emëruesin e saj me faktorin më të lartë të përbashkët (HCF). Le të themi, në shembullin e mësipërm, thyesa e parë \(\frac{1}{2}\) është në formën e saj më të thjeshtë pasi 1 dhe 2 nuk kanë asnjë faktor të përbashkët përveç një; thyesa e dytë \(\frac{2}{4}\) nuk është në formën e saj më të thjeshtë, sepse 2 dhe 4 kanë dy faktorë të përbashkët - 1 dhe 2, nëse pjesëtojmë 2 dhe 4 me faktorin më të lartë të përbashkët dmth 2 atëherë \(\frac{2}{4}\) do të bëhet \(\frac{1}{2}\) që tani është forma më e thjeshtë e fraksionit.