Ett bråk är en del av en helhet. Ett komplett eller helt objekt är en helhet. En helhet kan vara en grupp av objekt eller ett enda objekt. När vi delar en hel sak i lika delar, då kallas varje del en bråkdel.
På bilden nedan är ett helt äpple uppdelat i två halvor. Varje halva är en bråkdel representerad som \(\frac{1}{2}\) där 1 är täljaren och 2 är nämnaren.

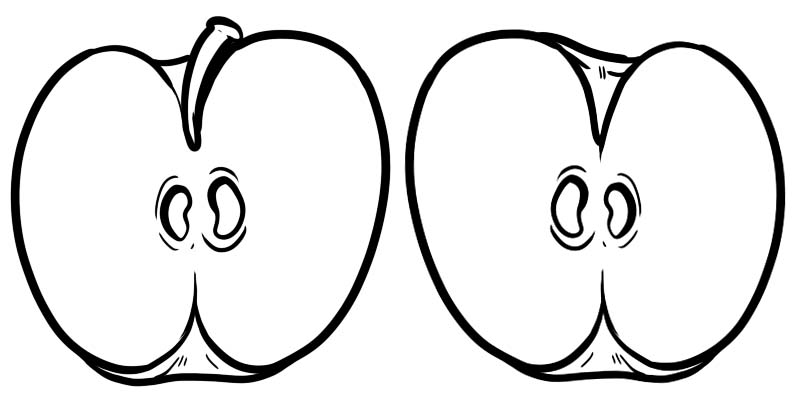
Ett bråk är uppbyggt av två tal som delas med en linje.
Siffran som skrivs under linjen kallas nämnaren. Nämnaren visar hur många lika delar något har delats upp i.
Siffran som skrivs ovanför raden kallas täljaren. Täljaren visar hur många delar av helheten som tas.
Täljaren kan vara större eller mindre än nämnaren.
Nämnaren är INTE lika med noll eller ett.
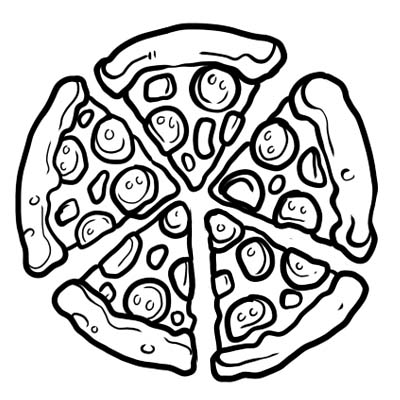
En pizza är uppdelad i fem lika stora delar. Om du bara äter en skiva av pizzan betyder det att du åt \(\frac{1}{5}\) av hela pizzan. \(\frac{1}{5}\) är bråket här.
Halvar och fjärdedelar
Harry och Jack var hungriga. De köpte en cupcake. De delade på cupcaken genom att dela den i två lika delar:

Här är del 1 och del 2 två delar av cupcaken. Del 1 är en halva och del 2 är en annan halva.
Kvartals (1/4) och trekvart (3/4)
Harry, Jack, Sam och Oliver köpte en chokladkaka. De skär den i 4 lika delar.
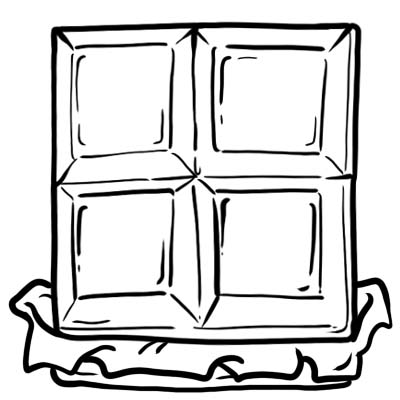
Varje del eller kub choklad är en fjärdedel, dvs. \(\frac{1}{4}\)
Det betyder en hel choklad uppdelad i fyra lika delar.
Anta att Jack åt sin del av chokladen, vi kan säga att han åt en fjärdedel eller \(\frac{1}{4}\) av chokladen. Hur mycket choklad är det kvar nu? 3 delar är kvar, så vi kan säga att \(\frac{3}{4}\) eller tre fjärdedelar av choklad är kvar.
Ta en titt på bilden nedan,
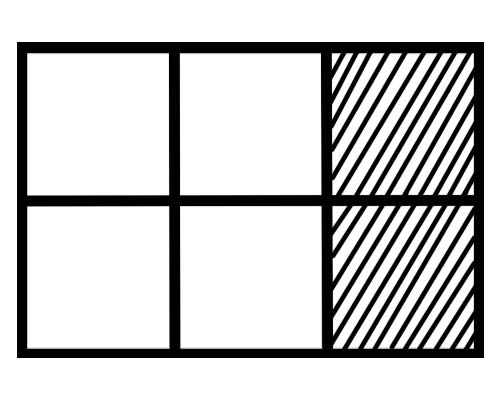
Vad är en bråkdel av varje del i denna figur? Det finns sex lika delar, så en bråkdel av varje del är \(\frac{1}{6}\) .
Hur många delar av helheten är skuggade i den givna figuren? 2 delar av de totalt 6 delarna är skuggade, så den totala bråkdelen är \(\frac{2}{6}\) .
Hur många delar av helheten är inte skuggade i den givna figuren? 4 delar av de totalt 6 delarna är inte skuggade, så den totala bråkdelen är \(\frac{4}{6}\) .
Vi kan också använda ett bråk för att representera en del av en grupp. Låt oss ta ett exempel på en klass med 12 elever och klassläraren vill dela upp klassen i 2 lika stora grupper. Varje grupp kommer att ha 6 elever. \(\frac{1}{2}\) av 12 är 6 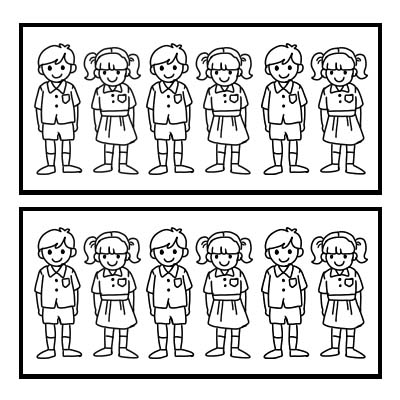
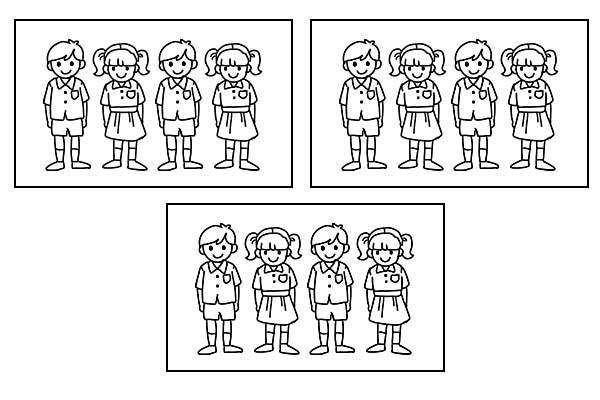
Om samma klass är indelad i 3 lika stora grupper kommer varje grupp att ha 4 elever. Eftersom \(\frac{1}{3}\) av 12 är 4.
Det finns olika typer av fraktioner som diskuteras nedan:
Rätta bråk
Ett eget bråk är ett tal som representerar en del av en helhet. I ett egenbråk visar siffran i nämnaren antalet delar som helheten är uppdelad i, medan siffran i täljaren visar antalet delar som har tagits. Ett eget bråk är ett bråk som är mindre än ett, med täljaren mindre än nämnaren.
Till exempel,
\(\frac{2}{5}\) dvs 2 delar av totalt 5 delar
\(\frac{3}{7}\) dvs 3 delar av totalt 7 delar
Oegentliga bråk
Ett bråk där täljaren är större än nämnaren kallas ett oegentligt bråk.
Till exempel,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….osv.
Blandade fraktioner
En kombination av en helhet och en del kallas en blandad fraktion.
Till exempel,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...etc.
Omvandling av en oegentlig fraktion till en blandad fraktion
Ett oegentligt bråk kan uttryckas som ett blandat bråk genom att dividera täljaren med nämnaren för det oegentliga bråket för att få kvoten och resten. Då blir den blandade fraktionen
Blandad bråkdel = Kvotient (Återstoden ∕ Divisor)
Omvandling av en blandad fraktion till en oegentlig fraktion
Ett blandat bråk kan skrivas i form av ett oegentligt bråk genom att skriva det på följande sätt:
[(Hel × Nämnare) + Täljare)] ∕ Nämnare
Som bråk
Bråk med samma nämnare sägs vara som bråk.
Till exempel,
\(\frac{3}{10}\) , \(\frac{4}{10}\) och \(\frac{7}{10}\) är som bråk
Till skillnad från bråk
Bråk med olika nämnare sägs vara till skillnad från bråk.
Till exempel,
\(\frac{3}{7}\) , \(\frac{5}{9}\) och \(\frac{2}{15}\) skiljer sig från bråk
Ekvivalenta fraktioner
Bråk som representerar samma del av en helhet sägs vara ekvivalenta bråk.
Till exempel,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Den enklaste formen av ett bråk
Ett bråk sägs vara i sin enklaste form eller sin lägsta form om dess täljare och nämnare inte har någon gemensam faktor förutom en. Den enklaste formen av ett bråk kan också hittas genom att dividera dess täljare och nämnare med dess högsta gemensamma faktor (HCF). Säg att i exemplet ovan är det första bråket \(\frac{1}{2}\) i sin enklaste form eftersom 1 och 2 inte har någon gemensam faktor förutom en; det andra bråket \(\frac{2}{4}\) är inte i sin enklaste form eftersom 2 och 4 har två gemensamma faktorer – 1 och 2, om vi dividerar 2 och 4 med den högsta gemensamma faktorn, dvs. 2, då \(\frac{2}{4}\) blir \(\frac{1}{2}\) vilket nu är den enklaste formen av bråket.