Sehemu ni sehemu ya jumla. Kitu kamili au kamili ni kizima. Jumla inaweza kuwa kikundi cha vitu au kitu kimoja. Tunapogawanya kitu kizima katika sehemu sawa, basi kila sehemu inaitwa sehemu.
Katika picha hapa chini, apple moja kamili imegawanywa katika nusu mbili. Kila nusu ni sehemu inayowakilishwa kama \(\frac{1}{2}\) ambapo 1 ni nambari na 2 ni kipunguzo.

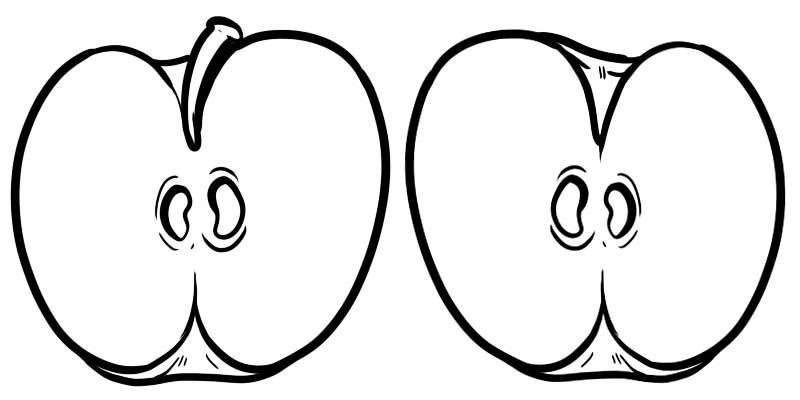
Sehemu inaundwa na nambari mbili ambazo zimegawanywa kwa mstari.
Nambari iliyoandikwa chini ya mstari inajulikana kama denominator. Denominata inaonyesha ni sehemu ngapi sawa kitu kimegawanywa.
Nambari iliyoandikwa juu ya mstari inajulikana kama nambari. Nambari inaonyesha ni sehemu ngapi za sehemu nzima zimechukuliwa.
Nambari inaweza kuwa kubwa au ndogo kuliko denominator.
Kipunguzo SI sawa na sifuri au moja.
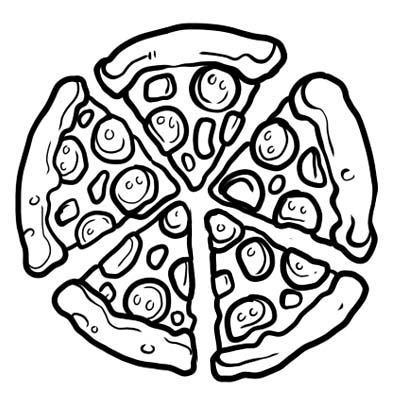
Pizza imegawanywa katika sehemu tano sawa. Ikiwa unakula kipande kimoja tu cha pizza, inamaanisha kuwa ulikula \(\frac{1}{5}\) ya pizza nzima. \(\frac{1}{5}\) ndio sehemu hapa.
Nusu na Robo
Harry na Jack walikuwa na njaa. Walinunua keki. Walishiriki keki kwa kuigawanya katika sehemu mbili sawa:

Hapa, Sehemu ya 1 na Sehemu ya 2 ni sehemu mbili za keki. Sehemu ya 1 ni nusu moja na Sehemu ya 2 ni nusu nyingine.
Robo (1/4) na Robo Tatu (3/4)
Harry, Jack, Sam, na Oliver walinunua baa ya chokoleti. Wanaukata katika sehemu 4 sawa.
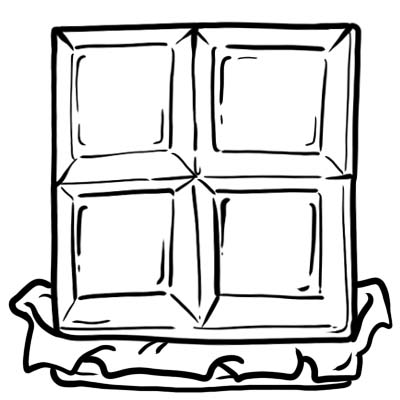
Kila sehemu au mchemraba wa chokoleti ni robo moja yaani \(\frac{1}{4}\)
Hii ina maana, chocolate moja nzima imegawanywa katika sehemu nne sawa.
Tuseme, Jack alikula sehemu yake ya chokoleti, tunaweza kusema alikula robo moja au \(\frac{1}{4}\) ya chokoleti. Ni chokoleti ngapi sasa imesalia? Sehemu 3 zimesalia, kwa hivyo tunaweza kusema kwamba \(\frac{3}{4}\) au robo tatu ya chokoleti imesalia.
Angalia takwimu iliyotolewa hapa chini,
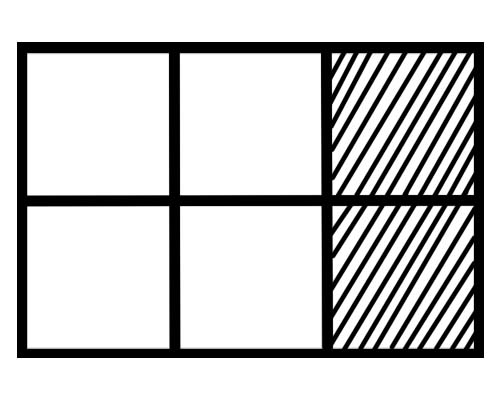
Je! ni sehemu gani ya kila sehemu katika takwimu hii? Kuna sehemu sita zinazofanana, kwa hivyo sehemu ya kila sehemu ni \(\frac{1}{6}\) .
Je! ni sehemu ngapi za sehemu nzima iliyotiwa kivuli kwenye takwimu iliyopewa? Sehemu 2 za jumla ya sehemu 6 zimetiwa kivuli, kwa hivyo jumla ya sehemu ni \(\frac{2}{6}\) .
Ni sehemu ngapi za nzima ambazo hazijatiwa kivuli kwenye takwimu iliyotolewa? Sehemu 4 za jumla ya sehemu 6 hazina kivuli, kwa hivyo jumla ya sehemu ni \(\frac{4}{6}\) .
Tunaweza pia kutumia sehemu kuwakilisha sehemu ya kikundi. Hebu tuchukue mfano wa darasa lenye wanafunzi 12 na mwalimu wa darasa anataka kuligawa darasa katika makundi 2 sawa. Kila kikundi kitakuwa na wanafunzi 6. \(\frac{1}{2}\) ya 12 ni 6 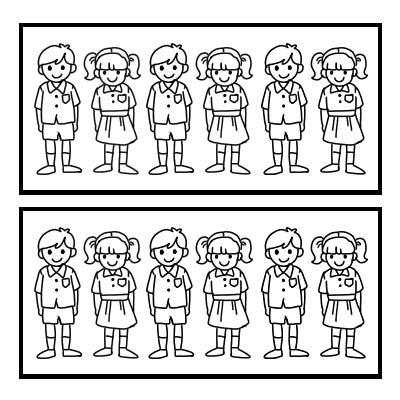
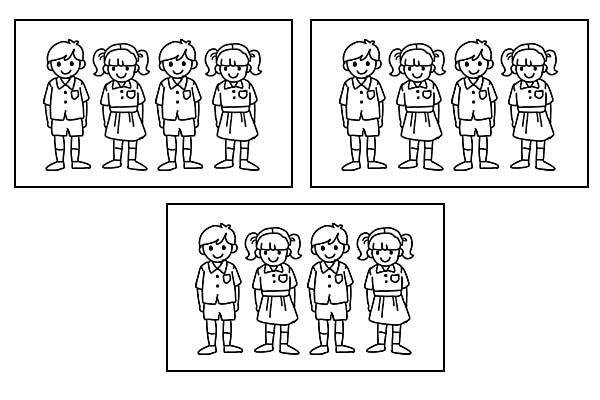
Ikiwa darasa moja litagawanywa katika vikundi 3 sawa, kila kikundi kitakuwa na wanafunzi 4. Kama \(\frac{1}{3}\) ya 12 ni 4.
Kuna aina tofauti za sehemu kama ilivyojadiliwa hapa chini:
Sehemu zinazofaa
Sehemu sahihi ni nambari inayowakilisha sehemu ya jumla. Katika sehemu inayofaa, nambari katika dhehebu inaonyesha idadi ya sehemu ambazo nzima imegawanywa, wakati nambari katika nambari inaonyesha idadi ya sehemu ambazo zimechukuliwa. Sehemu inayofaa ni sehemu ambayo ni chini ya moja, na nambari ni chini ya denominator.
Kwa mfano,
\(\frac{2}{5}\) yaani sehemu 2 kati ya jumla ya sehemu 5
\(\frac{3}{7}\) yaani sehemu 3 kati ya jumla ya sehemu 7
Sehemu zisizofaa
Sehemu ambayo nambari ni kubwa kuliko denominator inaitwa sehemu isiyofaa.
Kwa mfano,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ....nk.
Vipande vilivyochanganywa
Mchanganyiko wa sehemu nzima na sehemu inaitwa sehemu iliyochanganywa.
Kwa mfano,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...n.k.
Ubadilishaji wa sehemu isiyofaa kuwa sehemu iliyochanganywa
Sehemu isiyofaa inaweza kuonyeshwa kama sehemu iliyochanganywa kwa kugawanya nambari na denominator ya sehemu isiyofaa ili kupata mgawo na salio. Kisha sehemu iliyochanganywa itakuwa
Sehemu Mseto = Nukuu (Salio ∕ Kigawanyiko)
Ubadilishaji wa sehemu iliyochanganywa kuwa sehemu isiyofaa
Sehemu iliyochanganywa inaweza kuandikwa kwa namna ya sehemu isiyofaa kwa kuiandika kwa njia ifuatayo:
[(Nzima × Denominator) + Numerator)] ∕ Denominator
Kama sehemu
Visehemu vilivyo na dhehebu sawa vinasemekana kuwa kama visehemu.
Kwa mfano,
\(\frac{3}{10}\) , \(\frac{4}{10}\) na \(\frac{7}{10}\) ni kama sehemu
Tofauti na sehemu
Visehemu vilivyo na madhehebu tofauti vinasemekana kuwa tofauti na visehemu.
Kwa mfano,
\(\frac{3}{7}\) , \(\frac{5}{9}\) na \(\frac{2}{15}\) hazifanani na sehemu
Sehemu zinazolingana
Visehemu vinavyowakilisha sehemu sawa ya sehemu nzima vinasemekana kuwa visehemu sawa.
Kwa mfano,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Fomu rahisi zaidi ya sehemu
Sehemu inasemekana kuwa katika umbo lake rahisi zaidi au umbo lake la chini kabisa ikiwa nambari na kiashiria chake havina sababu ya kawaida isipokuwa moja. Njia rahisi zaidi ya sehemu pia inaweza kupatikana kwa kugawanya nambari yake na denominator kwa sababu yake ya juu zaidi (HCF). Sema, katika mfano ulio hapo juu, sehemu ya kwanza \(\frac{1}{2}\) iko katika umbo lake rahisi kwani 1 na 2 hazina sababu za kawaida isipokuwa moja; sehemu ya pili \(\frac{2}{4}\) haiko katika umbo lake rahisi zaidi kwa sababu 2 na 4 zina mambo mawili ya kawaida - 1 na 2, ikiwa tutagawanya 2 na 4 kwa kipengele cha juu zaidi cha kawaida yaani 2 basi \(\frac{2}{4}\) itakuwa \(\frac{1}{2}\) ambayo sasa ndiyo aina rahisi zaidi ya sehemu.