เศษส่วนเป็นส่วนหนึ่งของทั้งหมด วัตถุที่สมบูรณ์หรือเต็มคือทั้งหมด ทั้งหมดสามารถเป็นกลุ่มของวัตถุหรือวัตถุเดียว เมื่อเราแบ่งสิ่งทั้งหมดออกเป็นส่วนเท่า ๆ กัน แล้วแต่ละส่วนจะเรียกว่าเศษส่วน
ในภาพด้านล่าง แอปเปิ้ลเต็มหนึ่งผลถูกแบ่งออกเป็นสองส่วน แต่ละครึ่งเป็นเศษส่วนที่แสดงเป็น \(\frac{1}{2}\) โดยที่ 1 เป็นตัวเศษและ 2 เป็นตัวส่วน

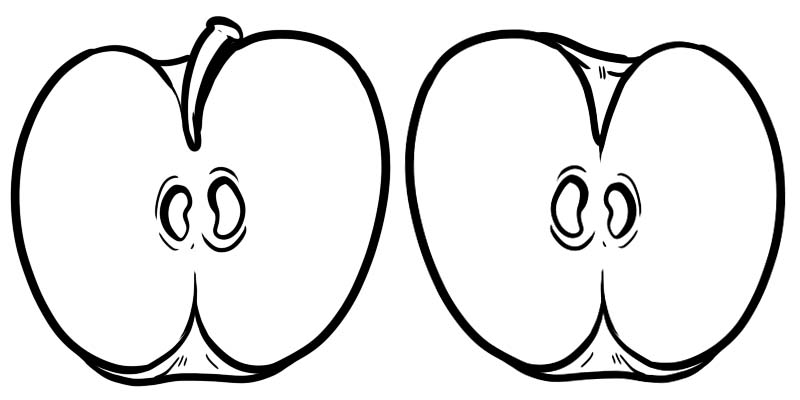
เศษส่วนประกอบด้วยตัวเลขสองตัวที่หารด้วยเส้นตรง
ตัวเลขที่เขียนใต้บรรทัดเรียกว่าตัวส่วน ตัวส่วนแสดงให้เห็นว่าสิ่งที่ถูกแบ่งออกเป็นส่วนเท่า ๆ กันกี่ส่วน
ตัวเลขที่เขียนไว้เหนือบรรทัดเรียกว่าตัวเศษ ตัวเศษแสดงจำนวนส่วนที่ถ่ายทั้งหมด
ตัวเศษสามารถมากกว่าหรือเล็กกว่าตัวส่วนได้
ตัวส่วนไม่เท่ากับศูนย์หรือหนึ่ง
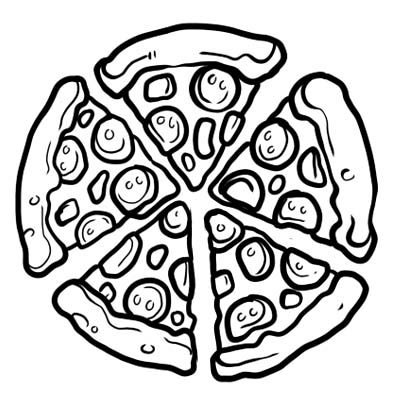
พิซซ่าแบ่งออกเป็นห้าส่วนเท่า ๆ กัน หากคุณกินพิซซ่าเพียงชิ้นเดียว หมายความว่าคุณกิน \(\frac{1}{5}\) ของพิซซ่าทั้งหมด \(\frac{1}{5}\) คือเศษส่วนตรงนี้
แบ่งครึ่งและไตรมาส
แฮร์รี่และแจ็คกำลังหิว พวกเขาซื้อคัพเค้ก พวกเขาแบ่งปันคัพเค้กโดยแบ่งออกเป็นสองส่วนเท่า ๆ กัน:

ในที่นี้ ส่วนที่ 1 และส่วนที่ 2 เป็นเศษส่วนของคัพเค้กสองส่วน ส่วนที่ 1 เป็นครึ่งหนึ่งและส่วนที่ 2 เป็นอีกครึ่งหนึ่ง
ไตรมาส (1/4) และสามในสี่ (3/4)
แฮร์รี่ แจ็ค แซม และโอลิเวอร์ซื้อช็อกโกแลตแท่งหนึ่ง พวกเขาตัดมันออกเป็น 4 ส่วนเท่า ๆ กัน
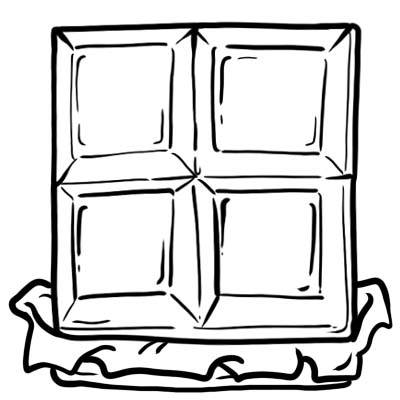
ช็อกโกแลตแต่ละส่วนหรือลูกบาศก์คือหนึ่งในสี่ เช่น \(\frac{1}{4}\)
หมายความว่า ช็อกโกแลตทั้งหมด 1 ชิ้น แบ่งออกเป็น 4 ส่วนเท่าๆ กัน
สมมุติว่าแจ็คกินช็อกโกแลตในส่วนของเขา เราสามารถพูดได้ว่าเขากินช็อกโกแลตหนึ่งในสี่หรือ \(\frac{1}{4}\) ตอนนี้ช็อกโกแลตเหลือเท่าไหร่? เหลืออีก 3 ส่วน เราสามารถพูดได้ว่า \(\frac{3}{4}\) หรือช็อกโกแลตเหลือสามในสี่
ดูรูปที่ให้ไว้ด้านล่าง
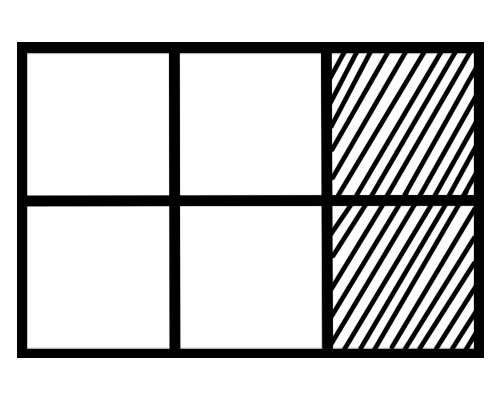
อะไรคือเศษส่วนของแต่ละส่วนในรูปนี้? มีหกส่วนเท่าๆ กัน ดังนั้นเศษของแต่ละส่วนคือ \(\frac{1}{6}\)
จากภาพที่กำหนดให้แรเงาทั้งหมดมีกี่ส่วน? 2 ส่วนของทั้งหมด 6 ส่วนถูกแรเงา ดังนั้นเศษส่วนทั้งหมดคือ \(\frac{2}{6}\)
ในรูปที่กำหนดมีทั้งหมดกี่ส่วนที่ไม่ได้แรเงา? 4 ส่วนจากทั้งหมด 6 ส่วนไม่มีการแรเงา ดังนั้นเศษส่วนทั้งหมดคือ \(\frac{4}{6}\)
เรายังใช้เศษส่วนแทนส่วนของกลุ่มได้อีกด้วย ยกตัวอย่างชั้นเรียนที่มีนักเรียน 12 คน และครูประจำชั้นต้องการแบ่งชั้นเรียนออกเป็น 2 กลุ่มเท่าๆ กัน แต่ละกลุ่มจะมีนักเรียน 6 คน \(\frac{1}{2}\) จาก 12 คือ 6 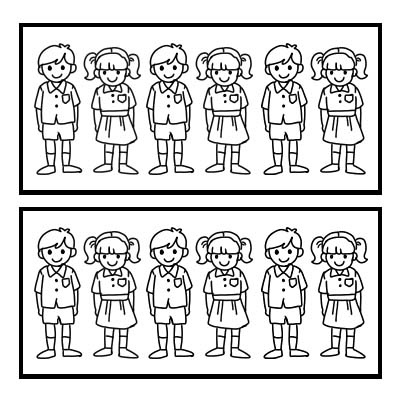
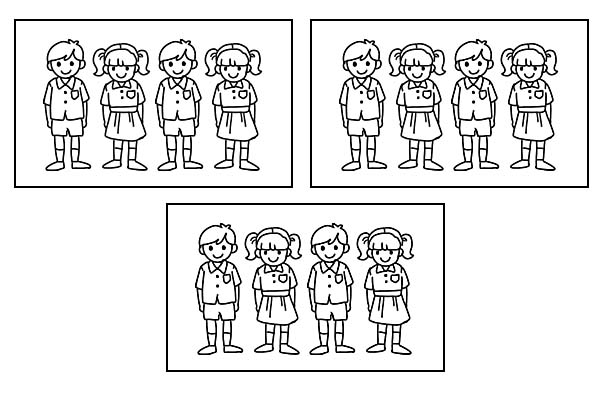
ถ้าคลาสเดียวกันแบ่งเป็น 3 กลุ่มเท่าๆ กัน แต่ละกลุ่มจะมีนักเรียน 4 คน เนื่องจาก \(\frac{1}{3}\) ของ 12 คือ 4
เศษส่วนมีหลายประเภทตามที่กล่าวไว้ด้านล่าง:
เศษส่วนที่เหมาะสม
เศษส่วนที่เหมาะสมคือตัวเลขที่แสดงส่วนหนึ่งของจำนวนเต็ม ในรูปเศษส่วนที่เหมาะสม ตัวเลขในตัวส่วนจะแสดงจำนวนส่วนที่มีการหารทั้งหมด ขณะที่ตัวเลขในตัวเศษจะแสดงจำนวนส่วนที่ถ่ายไปแล้ว เศษส่วนที่เหมาะสมคือเศษส่วนที่น้อยกว่าหนึ่งโดยมีตัวเศษน้อยกว่าตัวส่วน
ตัวอย่างเช่น,
\(\frac{2}{5}\) คือ 2 ส่วนจากทั้งหมด 5 ส่วน
\(\frac{3}{7}\) คือ 3 ส่วนจากทั้งหมด 7 ส่วน
เศษส่วนไม่ถูกต้อง
เศษส่วนที่ตัวเศษมากกว่าตัวส่วนเรียกว่าเศษส่วนที่ไม่เหมาะสม
ตัวอย่างเช่น,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….ฯลฯ.
เศษส่วนผสม
การรวมของทั้งหมดและส่วนหนึ่งเรียกว่าเศษส่วนผสม
ตัวอย่างเช่น,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...ฯลฯ
การแปลงเศษส่วนเกินให้เป็นเศษส่วนผสม
เศษส่วนที่ไม่เหมาะสมสามารถแสดงเป็นเศษส่วนผสมได้โดยการหารตัวเศษด้วยตัวส่วนของเศษที่ไม่เหมาะสมเพื่อให้ได้ผลหารและเศษที่เหลือ จากนั้นเศษผสมจะเป็น
เศษส่วนคละ = ผลหาร (เศษส่วน ∕ ตัวหาร)
การแปลงเศษส่วนคละให้เป็นเศษเกิน
เศษส่วนผสมสามารถเขียนในรูปของเศษส่วนที่ไม่เหมาะสมได้โดยการเขียนด้วยวิธีต่อไปนี้:
[(ทั้งหมด × ตัวส่วน) + ตัวเศษ)] ∕ ตัวส่วน
ชอบเศษส่วน
เศษส่วนที่มีตัวส่วนเท่ากันเรียกว่าเศษส่วน
ตัวอย่างเช่น,
\(\frac{3}{10}\) , \(\frac{4}{10}\) และ \(\frac{7}{10}\) เป็นเหมือนเศษส่วน
ไม่เหมือนกับเศษส่วน
เศษส่วนที่มีตัวส่วนต่างกันเรียกว่าเศษส่วน
ตัวอย่างเช่น,
\(\frac{3}{7}\) , \(\frac{5}{9}\) และ \(\frac{2}{15}\) ไม่เหมือนกับเศษส่วน
เศษส่วนเทียบเท่า
เศษส่วนที่แทนส่วนเดียวกันของทั้งหมดเรียกว่าเศษส่วนที่เท่ากัน
ตัวอย่างเช่น,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
รูปแบบที่ง่ายที่สุดของเศษส่วน
กล่าวได้ว่าเศษส่วนจะอยู่ในรูปแบบที่ง่ายที่สุดหรือน้อยที่สุดถ้าตัวเศษและตัวส่วนไม่มีตัวประกอบร่วมกันยกเว้นตัวเดียว รูปแบบเศษส่วนที่ง่ายที่สุดสามารถพบได้โดยการหารตัวเศษและตัวหารด้วยตัวประกอบร่วมสูงสุด (HCF) สมมติว่าในตัวอย่างข้างต้น เศษส่วนแรก \(\frac{1}{2}\) อยู่ในรูปแบบที่ง่ายที่สุด เนื่องจาก 1 และ 2 ไม่มีตัวประกอบร่วมยกเว้นเพียงตัวเดียว เศษส่วนที่สอง \(\frac{2}{4}\) ไม่ได้อยู่ในรูปแบบที่ง่ายที่สุดเพราะ 2 และ 4 มีตัวประกอบร่วมสองตัว – 1 และ 2 หากเราหาร 2 และ 4 ด้วยตัวประกอบร่วมสูงสุดเช่น 2 แล้ว \(\frac{2}{4}\) จะกลายเป็น \(\frac{1}{2}\) ซึ่งตอนนี้เป็นรูปแบบเศษส่วนที่ง่ายที่สุด