Ang fraction ay bahagi ng kabuuan. Ang isang kumpleto o buong bagay ay isang kabuuan. Ang isang kabuuan ay maaaring isang pangkat ng mga bagay o isang solong bagay. Kapag hinati natin ang isang buong bagay sa pantay na bahagi, ang bawat bahagi ay tinatawag na isang fraction.
Sa larawan sa ibaba, ang isang buong mansanas ay nahahati sa dalawang halves. Ang bawat kalahati ay isang fraction na kinakatawan bilang \(\frac{1}{2}\) kung saan 1 ang numerator at 2 ang denominator.

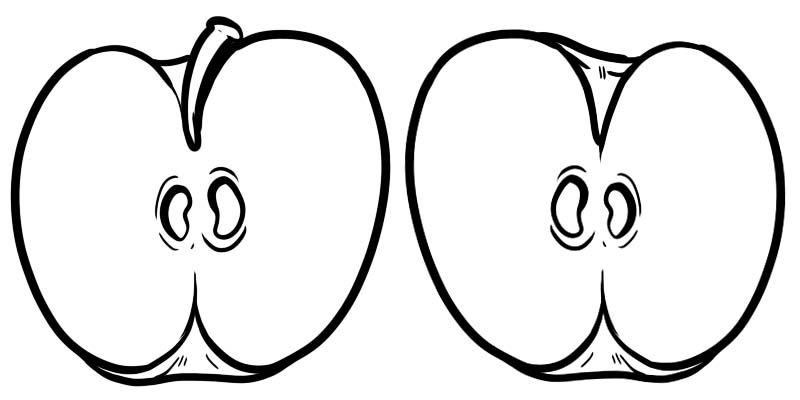
Ang isang fraction ay binubuo ng dalawang numero na hinati sa isang linya.
Ang bilang na nakasulat sa ibaba ng linya ay kilala bilang denominator. Ipinapakita ng denominator kung gaano karaming pantay na bahagi ang nahahati sa isang bagay.
Ang numerong nakasulat sa itaas ng linya ay kilala bilang numerator. Ang numerator ay nagpapakita kung gaano karaming bahagi ng kabuuan ang kinuha.
Ang numerator ay maaaring mas malaki o mas maliit kaysa sa denominator.
Ang denominator ay HINDI katumbas ng zero o isa.
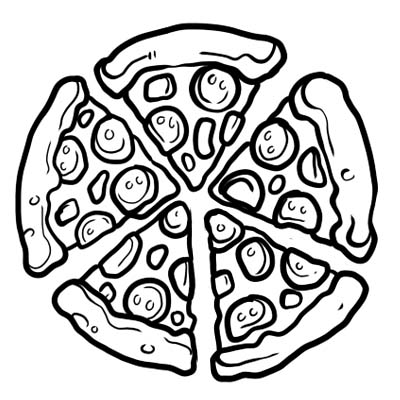
Ang isang pizza ay nahahati sa limang pantay na bahagi. Kung kumain ka lang ng isang slice ng pizza, ibig sabihin kumain ka \(\frac{1}{5}\) ng buong pizza. \(\frac{1}{5}\) ang fraction dito.
Halves at Quarters
Nagugutom sina Harry at Jack. Bumili sila ng cupcake. Ibinahagi nila ang cupcake sa pamamagitan ng paghahati nito sa dalawang pantay na bahagi:

Dito, ang Part 1 at Part 2 ay dalawang fraction ng cupcake. Ang Part 1 ay isang kalahati at ang Part 2 ay isa pang kalahati.
Quarters (1/4) at Three-Quarters (3/4)
Bumili sina Harry, Jack, Sam, at Oliver ng isang bar ng tsokolate. Pinutol nila ito sa 4 na pantay na bahagi.
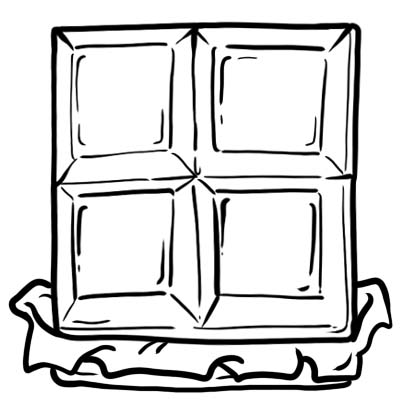
Ang bawat bahagi o cube ng tsokolate ay isang-kapat ie \(\frac{1}{4}\)
Ibig sabihin, ang isang buong tsokolate ay nahahati sa apat na pantay na bahagi.
Kumbaga, kinain ni Jack ang kanyang bahagi ng tsokolate, masasabi nating kumain siya ng one-fourth o \(\frac{1}{4}\) ng tsokolate. Ilang tsokolate ngayon ang natitira? 3 bahagi ang natitira, kaya masasabi nating \(\frac{3}{4}\) o tatlong-kapat ng tsokolate ang natitira.
Tingnan ang figure na ibinigay sa ibaba,
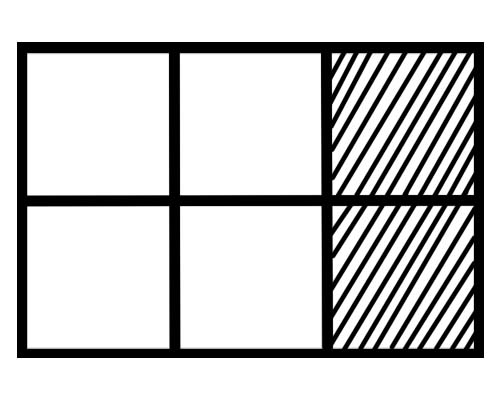
Ano ang isang fraction ng bawat bahagi sa figure na ito? Mayroong anim na pantay na bahagi, kaya ang isang fraction ng bawat bahagi ay \(\frac{1}{6}\) .
Ilang bahagi ng kabuuan ang may kulay sa ibinigay na pigura? 2 bahagi ng kabuuang 6 na bahagi ay may kulay, kaya ang kabuuang bahagi ay \(\frac{2}{6}\) .
Ilang bahagi ng kabuuan ang hindi nakakulay sa ibinigay na pigura? 4 na bahagi ng kabuuang 6 na bahagi ang hindi nakakulay, kaya ang kabuuang bahagi ay \(\frac{4}{6}\) .
Maaari din tayong gumamit ng fraction upang kumatawan sa isang bahagi ng isang pangkat. Kumuha tayo ng isang halimbawa ng isang klase na mayroong 12 mag-aaral at nais ng guro ng klase na hatiin ang klase sa 2 pantay na grupo. Bawat pangkat ay magkakaroon ng 6 na mag-aaral. \(\frac{1}{2}\) ng 12 ay 6 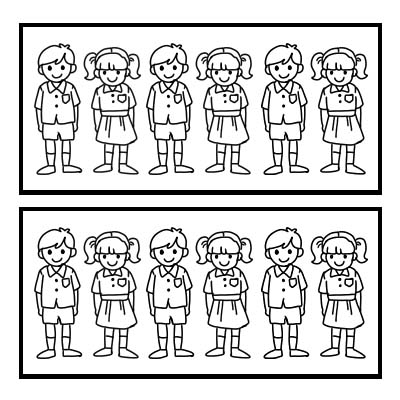
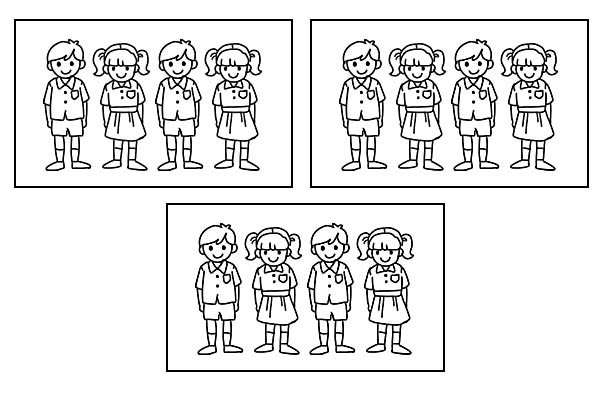
Kung ang parehong klase ay nahahati sa 3 pantay na grupo, bawat pangkat ay magkakaroon ng 4 na mag-aaral. Dahil ang \(\frac{1}{3}\) ng 12 ay 4.
Mayroong iba't ibang uri ng mga fraction tulad ng tinalakay sa ibaba:
Mga wastong fraction
Ang wastong fraction ay isang numero na kumakatawan sa isang bahagi ng isang kabuuan. Sa tamang fraction, ang numero sa denominator ay nagpapakita ng bilang ng mga bahagi kung saan ang kabuuan ay hinati, habang ang bilang sa numerator ay nagpapakita ng bilang ng mga bahagi na kinuha. Ang wastong fraction ay isang fraction na mas mababa sa isa, na ang numerator ay mas mababa sa denominator.
Halimbawa,
\(\frac{2}{5}\) ibig sabihin, 2 bahagi sa kabuuang 5 bahagi
\(\frac{3}{7}\) ibig sabihin, 3 bahagi sa kabuuang 7 bahagi
Mga hindi wastong fraction
Ang isang fraction kung saan ang numerator ay mas malaki kaysa sa denominator ay tinatawag na isang hindi wastong fraction.
Halimbawa,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….atbp.
Mga pinaghalong fraction
Ang kumbinasyon ng isang kabuuan at isang bahagi ay tinatawag na pinaghalong fraction.
Halimbawa,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...atbp.
Pag-convert ng hindi wastong fraction sa isang mixed fraction
Ang isang hindi wastong fraction ay maaaring ipahayag bilang isang mixed fraction sa pamamagitan ng paghahati ng numerator sa denominator ng hindi wastong fraction upang makuha ang quotient at ang natitira. Pagkatapos ay ang mixed fraction ay magiging
Mixed Fraction = Quotient (Natitirang ∕ Divisor)
Conversion ng isang mixed fraction sa isang improper fraction
Ang isang mixed fraction ay maaaring isulat sa anyo ng isang di-wastong fraction sa pamamagitan ng pagsulat nito sa sumusunod na paraan:
[(Buong × Denominator) + Numerator)] ∕ Denominator
Tulad ng mga fraction
Ang mga fraction na may parehong denominator ay sinasabing parang mga fraction.
Halimbawa,
\(\frac{3}{10}\) , \(\frac{4}{10}\) at \(\frac{7}{10}\) ay parang mga fraction
Hindi tulad ng mga fraction
Ang mga fraction na may iba't ibang denominator ay sinasabing hindi katulad ng mga fraction.
Halimbawa,
\(\frac{3}{7}\) , \(\frac{5}{9}\) at \(\frac{2}{15}\) ay hindi katulad ng mga fraction
Mga katumbas na fraction
Ang mga fraction na kumakatawan sa parehong bahagi ng isang kabuuan ay sinasabing katumbas na mga fraction.
Halimbawa,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Ang pinakasimpleng anyo ng isang fraction
Ang isang fraction ay sinasabing nasa pinakasimpleng anyo o pinakamababang anyo nito kung ang numerator at denominator nito ay walang common factor maliban sa isa. Ang pinakasimpleng anyo ng isang fraction ay matatagpuan din sa pamamagitan ng paghahati ng numerator at denominator nito sa pinakamataas na common factor (HCF). Sabihin, sa halimbawa sa itaas, ang unang fraction \(\frac{1}{2}\) ay nasa pinakasimpleng anyo nito dahil ang 1 at 2 ay walang karaniwang salik maliban sa isa; ang pangalawang fraction \(\frac{2}{4}\) ay wala sa pinakasimpleng anyo nito dahil ang 2 at 4 ay may dalawang karaniwang salik - 1 at 2, kung hahatiin natin ang 2 at 4 sa pinakamataas na karaniwang salik ie 2 pagkatapos \(\frac{2}{4}\) ay magiging \(\frac{1}{2}\) na ngayon ang pinakasimpleng anyo ng fraction.