Kesir, bir bütünün parçasıdır. Tam veya tam bir nesne bir bütündür. Bütün, bir nesne grubu veya tek bir nesne olabilir. Bir bütünü eşit parçalara böldüğümüzde her parçaya kesir denir.
Aşağıdaki resimde, bir tam elma ikiye bölünmüştür. Her yarım, 1'in pay ve 2'nin payda olduğu \(\frac{1}{2}\) olarak temsil edilen bir kesirdir.

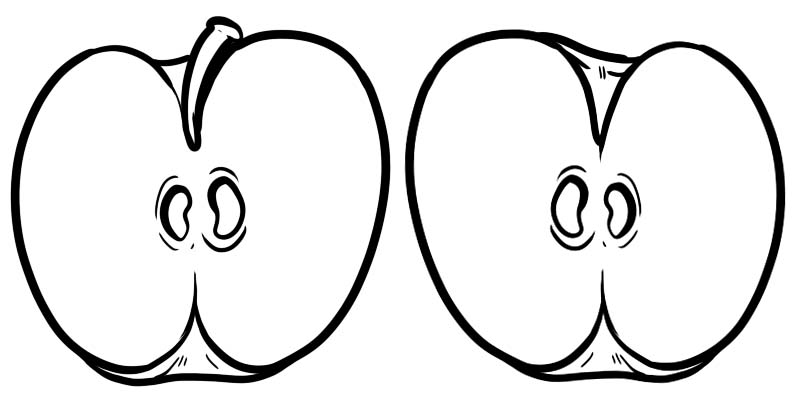
Kesir, bir çizgiyle bölünmüş iki sayıdan oluşur.
Çizginin altına yazılan sayı payda olarak bilinir. Payda, bir şeyin kaç eşit parçaya bölündüğünü gösterir.
Çizginin üzerine yazılan sayı pay olarak bilinir. Pay, bütünün kaç parçasının alındığını gösterir.
Pay, paydadan daha büyük veya daha küçük olabilir.
Payda sıfır veya bire eşit DEĞİLDİR.
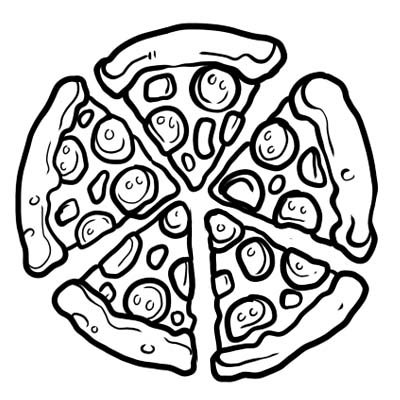
Bir pizza beş eşit parçaya bölünür. Pizzadan yalnızca bir dilim yerseniz, tüm pizzadan \(\frac{1}{5}\) yemişsiniz demektir. \(\frac{1}{5}\) buradaki kesirdir.
Yarılar ve Çeyrekler
Harry ve Jack açtılar. Bir kek aldılar. Keki iki eşit parçaya bölerek paylaştılar:

Burada, Kısım 1 ve Kısım 2, kekin iki fraksiyonudur. 1. Kısım bir yarımdır ve 2. Kısım diğer yarımdır.
Çeyrek (1/4) ve Dörtte Üç (3/4)
Harry, Jack, Sam ve Oliver bir kalıp çikolata aldılar. 4 eşit parçaya böldüler.
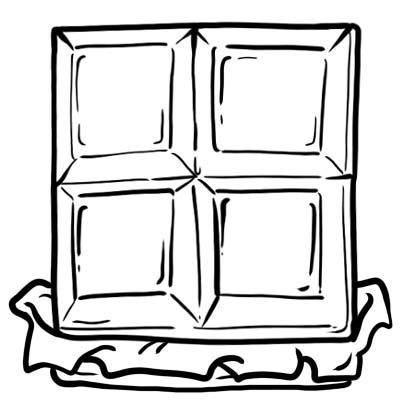
Çikolatanın her parçası veya küpü dörtte birdir, yani \(\frac{1}{4}\)
Bu, bir bütün çikolatanın dört eşit parçaya bölünmesi anlamına gelir.
Jack'in çikolatanın kendisine düşen kısmını yediğini varsayalım, çikolatanın dörtte birini veya \(\frac{1}{4}\) yediğini söyleyebiliriz. Şimdi ne kadar çikolata kaldı? 3 parça kaldı, yani çikolatanın \(\frac{3}{4}\) veya dörtte üçü kaldığını söyleyebiliriz.
Aşağıda verilen şekle bir göz atın,
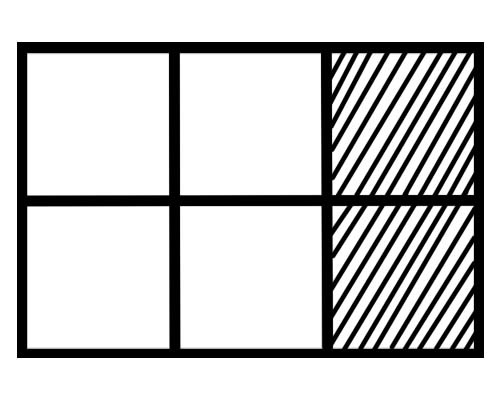
Bu şekildeki her bir parçanın kesri nedir? Altı eşit parça vardır, bu nedenle her parçanın kesri \(\frac{1}{6}\) olur.
Verilen şekilde bir bütünün kaç parçası gölgelendirilmiştir? Toplam 6 parçanın 2 bölümü gölgeli olduğundan toplam kesir \(\frac{2}{6}\) olur.
Verilen şekilde bir bütünün kaç parçası gölgeli değildir? Toplam 6 parçanın 4 bölümü gölgeli değil, yani toplam kesir \(\frac{4}{6}\) .
Bir grubun bir parçasını temsil etmek için kesri de kullanabiliriz. 12 kişilik bir sınıfı ele alalım ve sınıf öğretmeni sınıfı 2 eşit gruba ayırmak istiyor. Her grupta 6 öğrenci olacaktır. \(\frac{1}{2}\) /12 eşittir 6 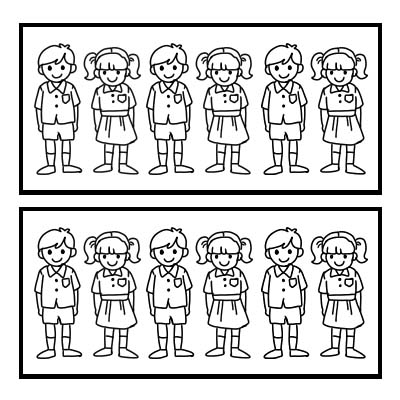
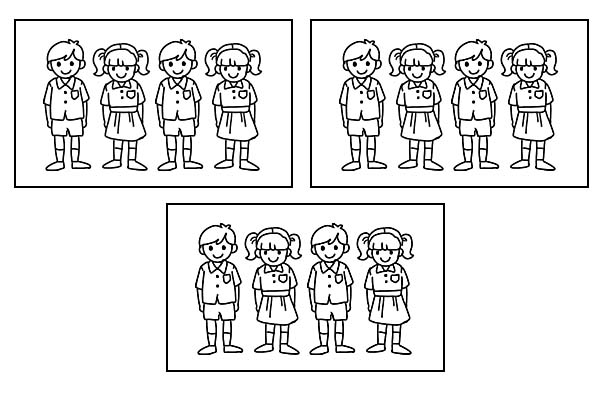
Aynı sınıf 3 eşit gruba ayrılırsa her grupta 4 öğrenci olacaktır. 12'nin \(\frac{1}{3}\) 'si 4 olduğu için.
Aşağıda tartışıldığı gibi farklı kesir türleri vardır:
uygun kesirler
Uygun bir kesir, bir bütünün bir parçasını temsil eden bir sayıdır. Uygun bir kesirde paydadaki sayı bütünün bölündüğü parça sayısını, paydaki sayı ise alınan parça sayısını gösterir. Uygun bir kesir, payı paydadan küçük olan birden küçük bir kesirdir.
Örneğin,
\(\frac{2}{5}\) yani toplam 5 parçadan 2 parça
\(\frac{3}{7}\) yani toplam 7 parçadan 3 parça
yanlış kesirler
Payı paydadan büyük olan kesre yanlış kesir denir.
Örneğin,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….vb.
Karışık kesirler
Bir bütün ve bir parçanın birleşimine karışık kesir denir.
Örneğin,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...vb.
Uygunsuz bir kesrin karışık bir kesre dönüştürülmesi
Uygun olmayan bir kesir, bölümü ve kalanı elde etmek için payın uygun olmayan kesrin paydasına bölünmesiyle karışık bir kesir olarak ifade edilebilir. Daha sonra karışık kesir olacak
Karışık Kesir = Bölüm (Kalan ∕ Bölen)
Karışık bir kesrin uygun olmayan bir kesre dönüştürülmesi
Karışık bir kesir, aşağıdaki şekilde yazılarak bileşik kesir şeklinde yazılabilir:
[(Tam × Payda) + Pay)] ∕ Payda
kesirler gibi
Paydaları aynı olan kesirlere benzer kesirler denir.
Örneğin,
\(\frac{3}{10}\) , \(\frac{4}{10}\) ve \(\frac{7}{10}\) kesirler gibidir
Kesirlerin aksine
Paydaları farklı olan kesirlere farklı kesirler denir.
Örneğin,
\(\frac{3}{7}\) , \(\frac{5}{9}\) ve \(\frac{2}{15}\) kesirlerden farklıdır
Eşdeğer kesirler
Bir bütünün aynı bölümünü temsil eden kesirlere eşdeğer kesirler denir.
Örneğin,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Bir kesrin en basit şekli
Bir kesrin payı ve paydasının birden başka ortak çarpanı yoksa, kesrin en basit veya en küçük biçiminde olduğu söylenir. Bir kesrin en basit şekli, payını ve paydasını en yüksek ortak çarpanına (HCF) bölerek de bulunabilir. Diyelim ki yukarıdaki örnekte, birinci kesir \(\frac{1}{2}\) en basit halindedir, çünkü 1 ve 2'nin birden başka ortak böleni yoktur; ikinci kesir \(\frac{2}{4}\) en basit biçiminde değildir çünkü 2 ve 4'ün iki ortak çarpanı vardır - 1 ve 2, eğer 2 ve 4'ü en yüksek ortak çarpana, yani 2'ye bölersek, o zaman \(\frac{2}{4}\) , artık kesrin en basit biçimi olan \(\frac{1}{2}\) haline gelecek.