Частка — це частина цілого. Цілісний або повний предмет є цілим. Ціле може бути групою об’єктів або одним об’єктом. Коли ми ділимо ціле на рівні частини, то кожна частина називається дробом.
На зображенні нижче одне повне яблуко розділене на дві половинки. Кожна половина — це дріб, представлений як \(\frac{1}{2}\) , де 1 — чисельник, а 2 — знаменник.

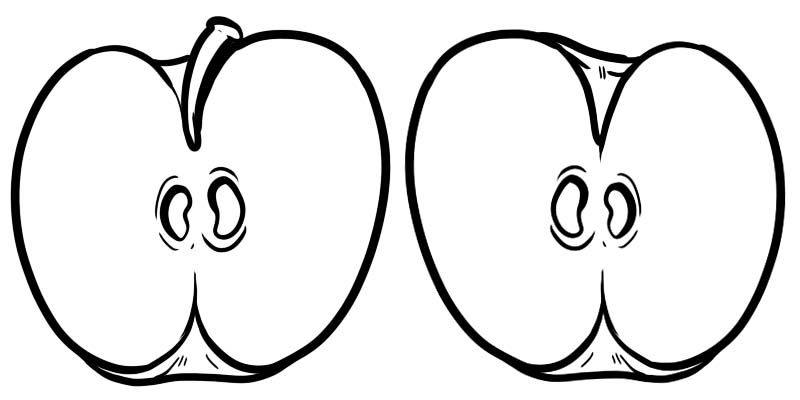
Дріб складається з двох чисел, розділених рискою.
Число, яке записане під рискою, називається знаменником. Знаменник показує, на скільки рівних частин щось поділено.
Число, написане над лінією, називається чисельником. Чисельник показує, скільки частин цілого взято.
Чисельник може бути більшим або меншим за знаменник.
Знаменник НЕ дорівнює нулю чи одиниці.
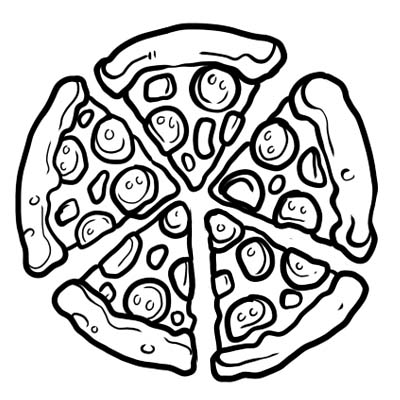
Піца ділиться на п'ять рівних частин. Якщо ви з’їли лише один шматок піци, це означає, що ви з’їли \(\frac{1}{5}\) усієї піци. \(\frac{1}{5}\) тут є дріб.
Половинки та Четвертини
Гаррі та Джек були голодні. Вони купили кекс. Вони поділили кекс, розділивши його на дві рівні частини:

Тут Частина 1 і Частина 2 — це дві частини кексу. Частина 1 — одна половина, а частина 2 — друга половина.
Чверті (1/4) і три чверті (3/4)
Гаррі, Джек, Сем і Олівер купили плитку шоколаду. Розрізають його на 4 рівні частини.
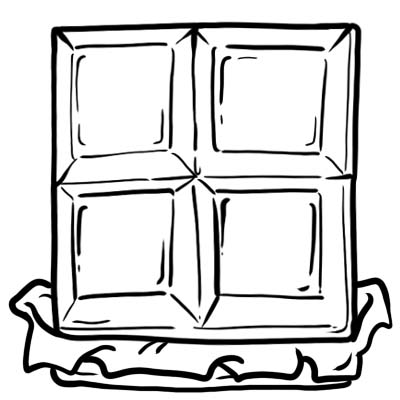
Кожна частина або кубик шоколаду становить одну чверть, тобто \(\frac{1}{4}\)
Це означає, що одна ціла шоколадка розділена на чотири рівні частини.
Припустимо, Джек з’їв свою частину шоколаду, ми можемо сказати, що він з’їв одну чверть або \(\frac{1}{4}\) шоколаду. Скільки шоколаду залишилося? Залишилося 3 частини, тому ми можемо сказати, що залишилося \(\frac{3}{4}\) або три чверті шоколаду.
Подивіться на малюнок нижче,
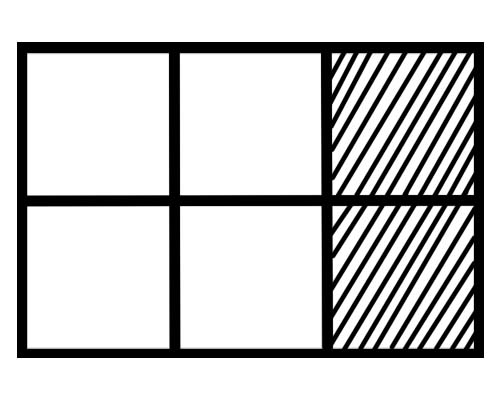
Чому дорівнює кожна частина цієї фігури? Є шість рівних частин, тому частка кожної частини дорівнює \(\frac{1}{6}\) .
Скільки частин цілого заштриховано на даному малюнку? 2 частини з 6 частин заштриховані, тому загальна частка дорівнює \(\frac{2}{6}\) .
Скільки частин цілого не заштриховано на даному малюнку? 4 частини із 6 частин не заштриховані, тому загальна частка дорівнює \(\frac{4}{6}\) .
Ми також можемо використовувати дріб, щоб представити частину групи. Візьмемо для прикладу клас, у якому 12 учнів, і класний керівник хоче розділити клас на 2 рівні групи. У кожній групі буде по 6 учнів. \(\frac{1}{2}\) з 12 дорівнює 6 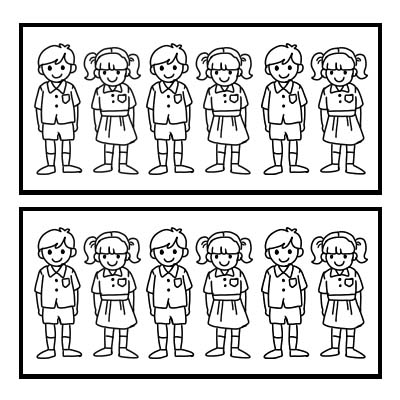
Якщо один клас розділити на 3 рівні групи, то в кожній групі буде по 4 учні. Оскільки \(\frac{1}{3}\) з 12 дорівнює 4.
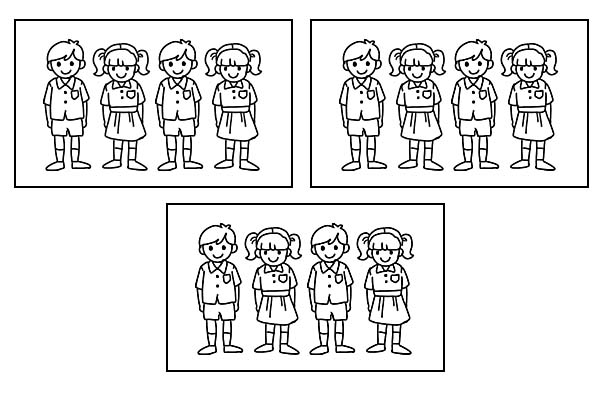
Існують різні типи дробів, про які йдеться нижче:
Правильні дроби
Правильний дріб — це число, яке представляє частину цілого. У правильному дробі число в знаменнику вказує на кількість частин, на які ділиться ціле, а число в чисельнику вказує на кількість частин, які були взяті. Правильний дріб – це дріб, менший від одиниці, чисельник якого менший від знаменника.
Наприклад,
\(\frac{2}{5}\) тобто 2 частини із загальної кількості 5 частин
\(\frac{3}{7}\) тобто 3 частини із загальної кількості 7 частин
Неправильні дроби
Дріб, у якого чисельник більший за знаменник, називається неправильним дробом.
Наприклад,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) … тощо.
Змішані дроби
З’єднання цілого і частини називають мішаним дробом.
Наприклад,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...і т.д.
Перетворення неправильного дробу в мішаний
Неправильний дріб можна виразити як змішаний дріб, поділивши чисельник на знаменник неправильного дробу, щоб отримати частку та залишок. Тоді буде змішана фракція
Змішана частка = частка (залишок ∕ дільник)
Перетворення мішаного дробу в неправильний
Мішаний дріб можна записати у вигляді неправильного дробу, записавши його так:
[(ціле × знаменник) + чисельник)] ∕ знаменник
Як дроби
Дроби з однаковими знаменниками називаються схожими на дроби.
Наприклад,
\(\frac{3}{10}\) , \(\frac{4}{10}\) і \(\frac{7}{10}\) схожі на дроби
На відміну від дробів
Дроби з різними знаменниками називаються несхожими дробами.
Наприклад,
\(\frac{3}{7}\) , \(\frac{5}{9}\) і \(\frac{2}{15}\) відрізняються від дробів
Рівнозначні дроби
Дроби, які представляють одну й ту саму частину цілого, називають еквівалентними дробами.
Наприклад,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Найпростіший вид дробу
Дріб називається найпростішим або найнижчим, якщо його чисельник і знаменник не мають спільного множника, крім одиниці. Найпростішу форму дробу також можна знайти, поділивши його чисельник і знаменник на старший спільний множник (HCF). Скажімо, у наведеному вище прикладі перший дріб \(\frac{1}{2}\) має найпростішу форму, оскільки 1 і 2 не мають спільного множника, крім одиниці; другий дріб \(\frac{2}{4}\) не має найпростішої форми, оскільки 2 і 4 мають два спільні множники – 1 і 2, якщо ми поділимо 2 і 4 на старший спільний множник, тобто 2, то \(\frac{2}{4}\) стане \(\frac{1}{2}\) що зараз є найпростішою формою дробу.