ایک حصہ پورے کا ایک حصہ ہے۔ ایک مکمل یا مکمل شے ایک مکمل ہے۔ ایک مکمل اشیاء کا ایک گروپ یا ایک شے ہو سکتا ہے۔ جب ہم کسی پوری چیز کو مساوی حصوں میں تقسیم کرتے ہیں، تو ہر حصے کو ایک حصہ کہا جاتا ہے۔
نیچے دی گئی تصویر میں، ایک مکمل سیب کو دو حصوں میں تقسیم کیا گیا ہے۔ ہر نصف ایک حصہ ہے جس کی نمائندگی \(\frac{1}{2}\) کے طور پر کی جاتی ہے جہاں 1 عدد ہے اور 2 ہرج ہے۔

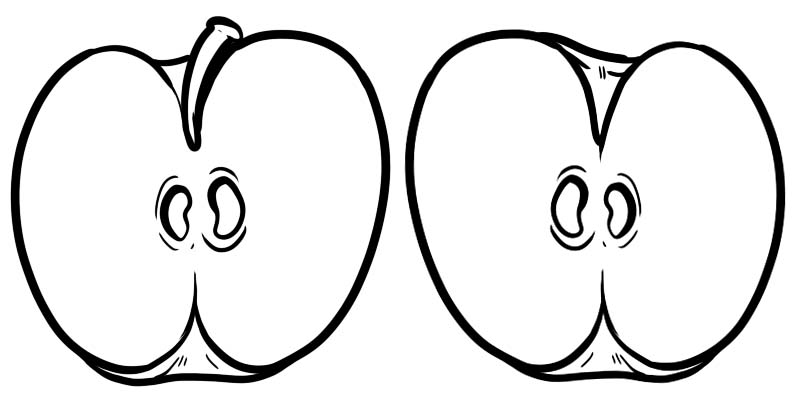
ایک حصہ دو نمبروں سے بنا ہوتا ہے جو ایک لائن سے تقسیم ہوتے ہیں۔
سطر کے نیچے لکھا ہوا نمبر ڈینومینیٹر کہلاتا ہے۔ ڈینومینیٹر دکھاتا ہے کہ کسی چیز کو کتنے برابر حصوں میں تقسیم کیا گیا ہے۔
لائن کے اوپر لکھا ہوا نمبر عدد کہلاتا ہے۔ عدد ظاہر کرتا ہے کہ پورے کے کتنے حصے لیے گئے ہیں۔
عدد ڈینومینیٹر سے بڑا یا چھوٹا ہو سکتا ہے۔
ڈینومینیٹر صفر یا ایک کے برابر نہیں ہے۔
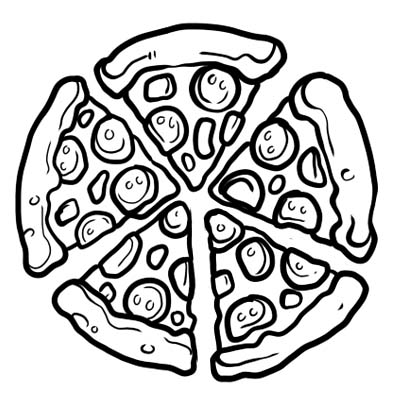
ایک پیزا کو پانچ برابر حصوں میں تقسیم کیا جاتا ہے۔ اگر آپ پیزا کا صرف ایک ٹکڑا کھاتے ہیں، تو اس کا مطلب ہے کہ آپ نے پورا پیزا \(\frac{1}{5}\) کھایا ہے۔ \(\frac{1}{5}\) یہاں کسر ہے۔
نصف اور چوتھائی
ہیری اور جیک بھوکے تھے۔ انہوں نے ایک کپ کیک خریدا۔ انہوں نے کپ کیک کو دو برابر حصوں میں تقسیم کرکے شیئر کیا:

یہاں، حصہ 1 اور حصہ 2 کپ کیک کے دو حصے ہیں۔ حصہ 1 نصف ہے اور حصہ 2 دوسرا نصف ہے۔
چوتھائی (1/4) اور تین چوتھائی (3/4)
ہیری، جیک، سیم، اور اولیور نے چاکلیٹ کا ایک بار خریدا۔ انہوں نے اسے 4 برابر حصوں میں کاٹ دیا۔
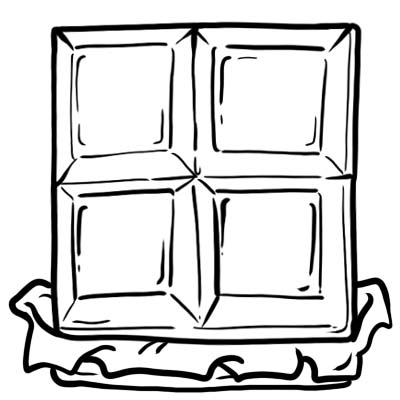
چاکلیٹ کا ہر حصہ یا کیوب ایک چوتھائی ہے یعنی \(\frac{1}{4}\)
اس کا مطلب ہے، ایک پوری چاکلیٹ کو چار برابر حصوں میں تقسیم کیا گیا ہے۔
فرض کریں، جیک نے چاکلیٹ کا اپنا حصہ کھایا، ہم کہہ سکتے ہیں کہ اس نے چاکلیٹ کا ایک چوتھائی یا \(\frac{1}{4}\) کھایا۔ اب کتنی چاکلیٹ رہ گئی ہے؟ 3 حصے باقی ہیں، اس لیے ہم کہہ سکتے ہیں کہ \(\frac{3}{4}\) یا تین چوتھائی چاکلیٹ رہ گئی ہے۔
ذیل میں دی گئی تصویر پر ایک نظر ڈالیں،
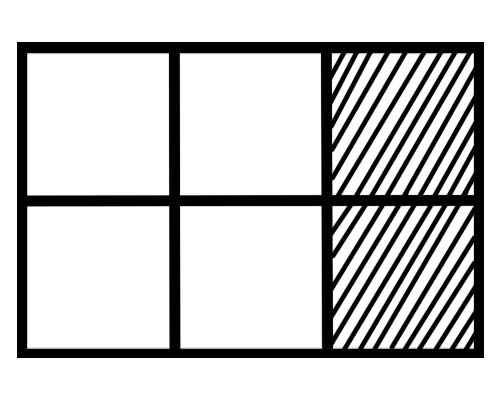
اس اعداد و شمار میں ہر حصے کا ایک حصہ کیا ہے؟ چھ برابر حصے ہیں، لہذا ہر حصے کا ایک حصہ ہے \(\frac{1}{6}\) ۔
دی گئی شکل میں پورے کے کتنے حصے سایہ دار ہیں؟ کل 6 حصوں میں سے 2 حصے سایہ دار ہیں، لہذا کل کسر ہے \(\frac{2}{6}\) ۔
دی گئی شکل میں پورے کے کتنے حصے سایہ دار نہیں ہیں؟ کل 6 حصوں میں سے 4 حصے سایہ دار نہیں ہیں، اس لیے کل کسر ہے \(\frac{4}{6}\) ۔
ہم کسی گروپ کے کسی حصے کی نمائندگی کرنے کے لیے ایک حصہ بھی استعمال کر سکتے ہیں۔ آئیے ایک کلاس کی مثال لیں جس میں 12 طلباء ہوں اور کلاس ٹیچر کلاس کو 2 برابر گروپوں میں تقسیم کرنا چاہتا ہے۔ ہر گروپ میں 6 طلباء ہوں گے۔ \(\frac{1}{2}\) از 12 ہے 6 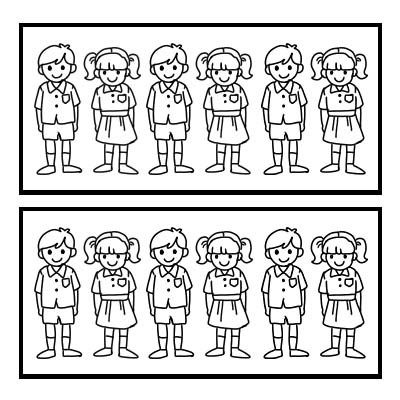
اگر ایک ہی کلاس کو 3 مساوی گروپوں میں تقسیم کیا جائے تو ہر گروپ میں 4 طلباء ہوں گے۔ جیسا کہ \(\frac{1}{3}\) 12 کا 4 ہے۔
مختلف قسم کے کسر ہیں جیسا کہ ذیل میں بحث کی گئی ہے۔
مناسب حصے
ایک مناسب حصہ ایک عدد ہے جو پورے کے ایک حصے کی نمائندگی کرتا ہے۔ ایک مناسب کسر میں، ڈینومینیٹر میں نمبر ان حصوں کی تعداد کو ظاہر کرتا ہے جن میں پورے کو تقسیم کیا گیا ہے، جبکہ عدد میں نمبر ان حصوں کی تعداد کو ظاہر کرتا ہے جو لیے گئے ہیں۔ مناسب کسر وہ حصہ ہوتا ہے جو ایک سے کم ہوتا ہے، جس کا ہندسہ ڈینومینیٹر سے کم ہوتا ہے۔
مثال کے طور پر،
\(\frac{2}{5}\) یعنی کل 5 حصوں میں سے 2 حصے
\(\frac{3}{7}\) یعنی کل 7 حصوں میں سے 3 حصے
غیر مناسب حصے
ایک ایسا حصہ جس میں ہندسہ ڈینومینیٹر سے بڑا ہو اسے نامناسب کسر کہا جاتا ہے۔
مثال کے طور پر،
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ....وغیرہ
مخلوط حصے
ایک مکمل اور ایک حصہ کے مجموعہ کو مخلوط کسر کہا جاتا ہے۔
مثال کے طور پر،
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...وغیرہ۔
ایک غلط حصہ کو مخلوط کسر میں تبدیل کرنا
عدد اور بقیہ کو حاصل کرنے کے لیے نامناسب کسر کو عدد کو نامناسب کسر کے ڈینومینیٹر سے تقسیم کر کے مخلوط کسر کے طور پر ظاہر کیا جا سکتا ہے۔ پھر ملا ہوا حصہ ہوگا۔
مخلوط کسر = حصّہ (بقیہ ∕ تقسیم)
مخلوط کسر کو غلط کسر میں تبدیل کرنا
مخلوط کسر کو مندرجہ ذیل طریقے سے لکھ کر غلط کسر کی شکل میں لکھا جا سکتا ہے۔
[(پورا × ڈینومینیٹر) + عدد)] ∕ ڈینومینیٹر
حصوں کی طرح
ایک ہی ڈینومینیٹر والے فریکشنز کو فریکشن کی طرح کہا جاتا ہے۔
مثال کے طور پر،
\(\frac{3}{10}\) ، \(\frac{4}{10}\) اور \(\frac{7}{10}\) حصوں کی طرح ہیں
حصوں کے برعکس
کہا جاتا ہے کہ مختلف ڈنومینیٹر والے فرکشن کو فرکشن کے برعکس کہا جاتا ہے۔
مثال کے طور پر،
\(\frac{3}{7}\) ، \(\frac{5}{9}\) اور \(\frac{2}{15}\) مختلف حصوں کے برعکس ہیں
مساوی حصے
وہ کسر جو پورے کے ایک ہی حصے کی نمائندگی کرتے ہیں ان کو مساوی کسر کہا جاتا ہے۔
مثال کے طور پر،
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
کسی کسر کی سادہ ترین شکل
ایک کسر کو اس کی سب سے آسان شکل یا اس کی سب سے کم شکل میں کہا جاتا ہے اگر اس کے ہندسوں اور ڈینومینیٹر میں ایک کے علاوہ کوئی عام فیکٹر نہ ہو۔ کسی کسر کی سب سے آسان شکل اس کے عدد اور ڈینومینیٹر کو اس کے اعلیٰ ترین عام فیکٹر (HCF) سے تقسیم کرکے بھی حاصل کی جاسکتی ہے۔ کہیے، اوپر کی مثال میں، پہلا کسر \(\frac{1}{2}\) اپنی سادہ ترین شکل میں ہے کیونکہ 1 اور 2 میں ایک کے علاوہ کوئی عام فیکٹر نہیں ہے۔ دوسرا کسر \(\frac{2}{4}\) اپنی سادہ ترین شکل میں نہیں ہے کیونکہ 2 اور 4 میں دو مشترک عامل ہیں - 1 اور 2، اگر ہم 2 اور 4 کو سب سے زیادہ عام فیکٹر یعنی 2 سے تقسیم کریں تو \(\frac{2}{4}\) بن جائے گا \(\frac{1}{2}\) جو اب کسر کی سب سے آسان شکل ہے۔