Kasr butunning bir qismidir. To'liq yoki to'liq ob'ekt bir butundir. Butun ob'ektlar guruhi yoki bitta ob'ekt bo'lishi mumkin. Agar butun narsani teng qismlarga ajratsak, har bir qism kasr deyiladi.
Quyidagi rasmda bitta to'liq olma ikkiga bo'lingan. Har bir yarmi kasr bo'lib \(\frac{1}{2}\) shaklida ifodalanadi, bunda 1 raqam va 2 maxrajdir.

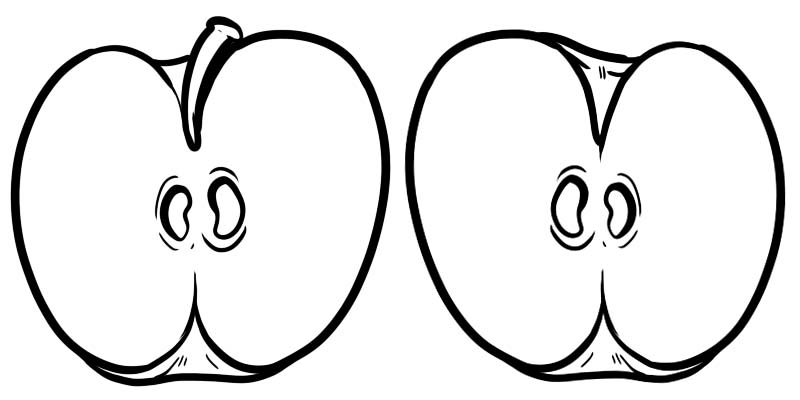
Kasr bir chiziqqa bo'lingan ikkita sondan iborat.
Chiziq ostida yozilgan raqam maxraj deb nomlanadi. Denominator narsaning nechta teng qismlarga bo'linganligini ko'rsatadi.
Chiziq tepasida yozilgan raqam hisoblagich deb nomlanadi. Numerator butunning nechta qismi olinganligini ko'rsatadi.
Numerator maxrajdan katta yoki kichik bo'lishi mumkin.
Maxraj nolga yoki birga EMAS.
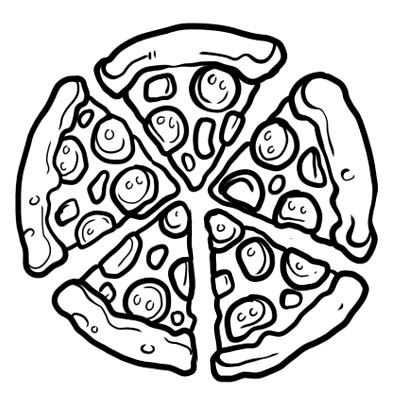
Pitsa beshta teng qismga bo'lingan. Agar siz pitsaning faqat bitta bo'lagini iste'mol qilsangiz, demak, siz butun pitsadan \(\frac{1}{5}\) yedingiz. \(\frac{1}{5}\) bu yerdagi kasr.
Yarim va chorak
Garri va Jek och edi. Ular keks sotib olishdi. Ular kekni ikkita teng qismga bo'lishdi:

Bu erda 1-qism va 2-qism kekning ikkita qismidir. 1-qism yarim, ikkinchi qism esa boshqa yarmi.
Chorak (1/4) va uch chorak (3/4)
Garri, Jek, Sem va Oliver bir bo'lak shokolad sotib olishdi. Ular uni 4 ta teng qismga bo'lishdi.
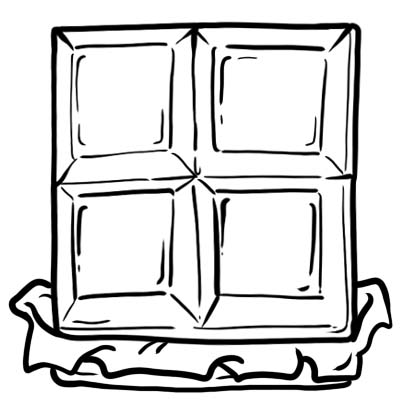
Shokoladning har bir qismi yoki kubi to'rtdan biriga teng, ya'ni \(\frac{1}{4}\)
Bu shuni anglatadiki, bitta shokolad to'rtta teng qismga bo'lingan.
Aytaylik, Jek shokoladning bir qismini yedi, deylik, u shokoladning to'rtdan bir qismini yoki \(\frac{1}{4}\) yedi. Hozir qancha shokolad qoldi? 3 qism qoldi, shuning uchun \(\frac{3}{4}\) yoki shokoladning to'rtdan uch qismi qolgan deb aytishimiz mumkin.
Quyidagi rasmga qarang,
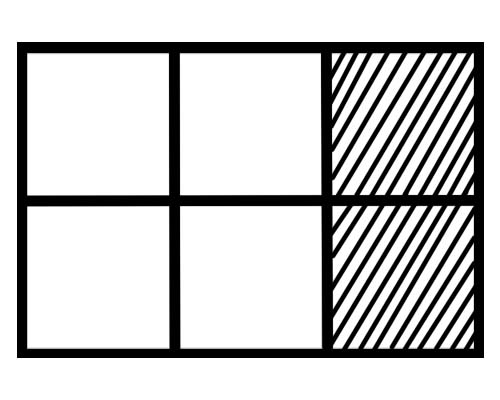
Ushbu rasmdagi har bir qismning qancha qismi? Oltita teng qism bor, shuning uchun har bir qismning bir qismi \(\frac{1}{6}\) ga teng.
Berilgan rasmda butunning nechta qismi soyalangan? Jami 6 qismning 2 qismi soyalangan, shuning uchun umumiy kasr \(\frac{2}{6}\) ga teng.
Berilgan rasmda butunning nechta qismi soyalanmagan? Jami 6 qismning 4 qismi soyali emas, shuning uchun umumiy kasr \(\frac{4}{6}\) ga teng.
Guruhning bir qismini ifodalash uchun kasrdan ham foydalanishimiz mumkin. Misol keltiraylik, sinfda 12 o'quvchi bor va sinf rahbari sinfni 2 ta teng guruhga bo'lishni xohlaydi. Har bir guruhda 6 nafardan talaba bo‘ladi. 12dan \(\frac{1}{2}\) 6 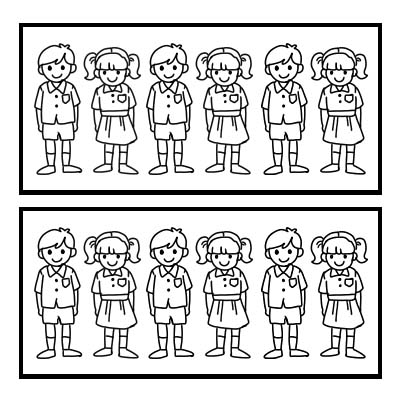
Agar bir sinf 3 ta teng guruhga bo'linsa, har bir guruhda 4 tadan o'quvchi bo'ladi. 12 dan \(\frac{1}{3}\) 4 ga teng.
Quyida muhokama qilingan fraksiyalarning har xil turlari mavjud:
To'g'ri kasrlar
To'g'ri kasr - bu butunning bir qismini ifodalovchi son. To'g'ri kasrda maxrajdagi raqam butun bo'linadigan qismlar sonini, hisoblagichdagi raqam esa olingan qismlar sonini ko'rsatadi. To'g'ri kasr - birdan kichik bo'lgan, soni maxrajdan kichik bo'lgan kasr.
Masalan,
\(\frac{2}{5}\) ya'ni jami 5 qismdan 2 qism
\(\frac{3}{7}\) ya'ni jami 7 qismdan 3 tasi
Noto'g'ri fraktsiyalar
Numeratori maxrajdan katta bo'lgan kasr noto'g'ri kasr deyiladi.
Masalan,
\(\frac{4}{3}\)
\(\frac{5}{2}\)
\(\frac{13}{8}\) ….va hokazo.
Aralash fraktsiyalar
Butun va qismning birikmasi aralash kasr deyiladi.
Masalan,
3 \(\frac{1}{2}\)
4 \(\frac{3}{4}\) ...va hokazo.
Noto'g'ri kasrni aralash kasrga aylantirish
Noto'g'ri kasrni aralash kasr sifatida ifodalash mumkin, bu bo'lim va qoldiqni olish uchun raqamni noto'g'ri kasrning maxrajiga bo'lish orqali amalga oshiriladi. Keyin aralash kasr bo'ladi
Aralash kasr = qism (qoldiq ∕ bo'linuvchi)
Aralash kasrni noto'g'ri kasrga aylantirish
Aralash kasrni quyidagi tarzda yozish orqali noto'g'ri kasr shaklida yozish mumkin:
[(Toʻliq × maxraj) + Numerator)] ∕ maxraj
Kasrlar kabi
Bir xil maxrajga ega bo'lgan kasrlar kasrlar kabi deyiladi.
Masalan,
\(\frac{3}{10}\) , \(\frac{4}{10}\) va \(\frac{7}{10}\) kasrlar kabidir
Kasrlardan farqli o'laroq
Turli xil maxrajli kasrlar kasrlarga o'xshamaydi, deyiladi.
Masalan,
\(\frac{3}{7}\) , \(\frac{5}{9}\) va \(\frac{2}{15}\) kasrlardan farq qiladi
Ekvivalent kasrlar
Butunning bir xil qismini ifodalovchi kasrlarga ekvivalent kasrlar deyiladi.
Masalan,
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\) = \(\frac{5}{10}\) = \(\frac{6}{12}\) …..
Kasrning eng oddiy shakli
Agar kasrning soni va maxrajida bittadan boshqa umumiy koʻrsatkich boʻlmasa, kasr eng oddiy yoki eng kichik koʻrinishda deyiladi. Kasrning eng oddiy shaklini uning soni va maxrajini eng yuqori umumiy koeffitsientiga (HCF) bo'lish orqali ham topish mumkin. Aytaylik, yuqoridagi misolda birinchi kasr \(\frac{1}{2}\) eng oddiy ko'rinishda, chunki 1 va 2 ning bittadan boshqa umumiy koeffitsienti yo'q; ikkinchi kasr \(\frac{2}{4}\) eng oddiy ko'rinishda emas, chunki 2 va 4 ikkita umumiy omilga ega - 1 va 2, agar 2 va 4 ni eng yuqori umumiy koeffitsientga bo'lsak, ya'ni 2 ga bo'lsa \(\frac{2}{4}\) \(\frac{1}{2}\) bo'ladi, bu hozir kasrning eng oddiy shakli.