علم المثلثات هو فرع من فروع الرياضيات يدرس العلاقة بين أضلاع وزوايا المثلث. تربط الدوال المثلثية بين زاوية المثلث وطول أضلاعه. هناك ست دوال مثلثية مرتبطة بمثلث الزاوية القائمة.
p عمودي ، h هو الوتر و b هو قاعدة الزاوية اليمنى ABC. ∆ ABC زاوية قائمة عند النقطة B و هي الزاوية المقابلة للضلع p.
الدوال الست المثلثية هي الجيب
\(\sin\theta =\) \(\frac{p}{h}\) = عمودي ∕ الوتر
\(\cos\theta = \) \(\frac{b}{h}\) = القاعدة ∕ الوتر
\(\tan\theta =\) \( \frac{p}{b}\) = عمودي ∕ قاعدة
لذلك \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
ومن ثم ، يمكننا استخدام حساب المثلثات لإيجاد الزوايا والأضلاع المفقودة في المثلث. دعنا نطبق دالة مثلثية لحل المسألة أدناه.
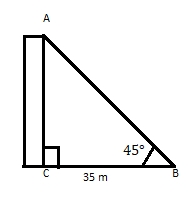
AC هو مبنى يصنع قمته زاوية 45 درجة على مسافة 35 مترًا من قدمه على مستوى أفقي. أوجد ارتفاع المبنى.
نعلم أن \(\tan\theta =\) عمودي
استخدم الآلة الحاسبة وأدخل قيمة الزاوية بالدرجات واضغط على الزر "sin" أو "cos" أو "tan". أو يمكنك استخدام جدول النسب المثلثية أدناه للعثور على قيمة \(\tan 45°\) .
| الدالة المثلثية | 0 درجة | 30 درجة | 45 درجة | 60 درجة | 90 درجة |
| الخطيئة | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| كوس | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| تان | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| سرير نقال | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| ثانية | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
يساعد جدول النسب المثلثية في إيجاد قيم الزوايا القياسية المثلثية مثل 0 ° و 30 ° و 45 ° و 60 ° و 90 °. وهو يتألف من النسب المثلثية - الجيب ، وجيب التمام ، والظل ، وقاطع التمام ، والقاطع ، والظل. يمكن كتابة هذه النسب باختصار مثل sin و cos و tan و cosec و sec و cot. تعتبر قيم النسب المثلثية للزوايا القياسية ضرورية لحل مسائل حساب المثلثات. لذلك ، من الضروري تذكر قيم النسب المثلثية لهذه الزوايا القياسية. استمرار المشكلة:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
الجواب: ارتفاع المبنى 35 م.
دائرة الوحدة نصف قطرها 1. يقع مركز الدائرة عند نقطة الأصل. إذن ، الطول من المركز إلى أي نقطة في الدائرة هو 1.
الإحداثيات عند أربع نقاط حيث يلتقي المحور بالدائرة هي (1،0) ، (0،1) ، (0 ، -1) ، (-1،0). لعمل زاوية موجبة ، نتحرك في اتجاه عكس عقارب الساعة ولزاوية سالبة ، نتحرك في اتجاه عقارب الساعة. دعونا نفكر في نقطة ذات إحداثيات (أ ، ب) على دائرة بعد تحريك الزاوية θ في اتجاه عكس اتجاه عقارب الساعة من المحور x. P هي نقطة على الدائرة ذات إحداثيات (أ ، ب). المثلث OPQ هو مثلث قائم الزاوية عند النقطة Q ، أي ∠ PQO = 90 درجة
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
يمكننا تمثيل الإحداثيات عند النقطة P على أنها (cosθ ، sinθ) . إذن ، جيب تمام يساوي إحداثيات x حيث يتقاطع الضلع النهائي للزاوية مع دائرة الوحدة وجيب يساوي إحداثيات y حيث يتقاطع الضلع النهائي للزاوية مع دائرة الوحدة. دعنا نحاول إيجاد قيمة إحداثي y عند النقطة A في دائرة الوحدة أدناه.
الجواب: إحداثي Y عند النقطة A هو \(\sin 270°\) .
تسمح لنا دائرة الوحدة بتوسيع مجال الجيب وجيب التمام ليشمل جميع الأعداد الحقيقية. عملية تحديد الجيب / جيب التمام لأي زاوية θ هي كما يلي: